Improving Uncertainty-Error Correspondence in Deep Bayesian Medical Image Segmentation

Increased usage of automated tools like deep learning in medical image segmentation has alleviated the bottleneck of manual contouring. This has shifted manual labour to quality assessment (QA) of automated contours which involves detecting errors and correcting them. A potential solution to semi-automated QA is to use deep Bayesian uncertainty to recommend potentially erroneous regions, thus reducing time spent on error detection. Previous work has investigated the correspondence between uncertainty and error, however, no work has been done on improving the "utility" of Bayesian uncertainty maps such that it is only present in inaccurate regions and not in the accurate ones. Our work trains the FlipOut model with the Accuracy-vs-Uncertainty (AvU) loss which promotes uncertainty to be present only in inaccurate regions. We apply this method on datasets of two radiotherapy body sites, c.f. head-and-neck CT and prostate MR scans. Uncertainty heatmaps (i.e. predictive entropy) are evaluated against voxel inaccuracies using Receiver Operating Characteristic (ROC) and Precision-Recall (PR) curves. Numerical results show that when compared to the Bayesian baseline the proposed method successfully suppresses uncertainty for accurate voxels, with similar presence of uncertainty for inaccurate voxels. Code to reproduce experiments is available at https://github.com/prerakmody/bayesuncertainty-error-correspondence

Accelerating hyperbolic t-SNE

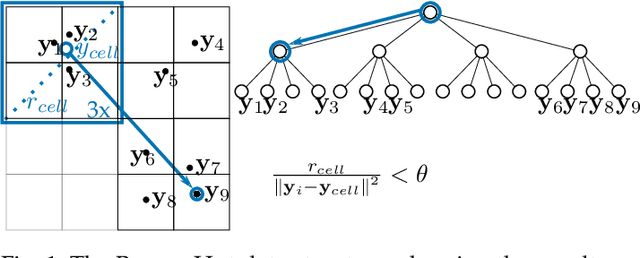
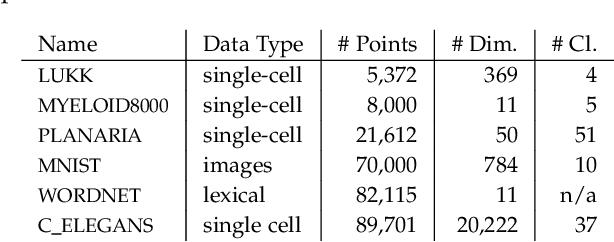
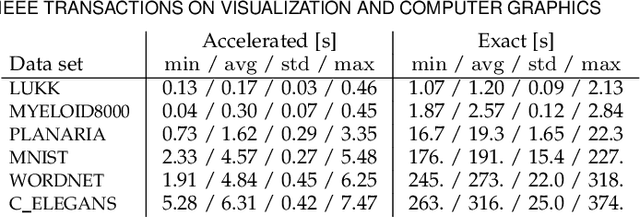
The need to understand the structure of hierarchical or high-dimensional data is present in a variety of fields. Hyperbolic spaces have proven to be an important tool for embedding computations and analysis tasks as their non-linear nature lends itself well to tree or graph data. Subsequently, they have also been used in the visualization of high-dimensional data, where they exhibit increased embedding performance. However, none of the existing dimensionality reduction methods for embedding into hyperbolic spaces scale well with the size of the input data. That is because the embeddings are computed via iterative optimization schemes and the computation cost of every iteration is quadratic in the size of the input. Furthermore, due to the non-linear nature of hyperbolic spaces, Euclidean acceleration structures cannot directly be translated to the hyperbolic setting. This paper introduces the first acceleration structure for hyperbolic embeddings, building upon a polar quadtree. We compare our approach with existing methods and demonstrate that it computes embeddings of similar quality in significantly less time. Implementation and scripts for the experiments can be found at https://graphics.tudelft.nl/accelerating-hyperbolic-tsne.

Tuning the perplexity for and computing sampling-based t-SNE embeddings

Widely used pipelines for the analysis of high-dimensional data utilize two-dimensional visualizations. These are created, e.g., via t-distributed stochastic neighbor embedding (t-SNE). When it comes to large data sets, applying these visualization techniques creates suboptimal embeddings, as the hyperparameters are not suitable for large data. Cranking up these parameters usually does not work as the computations become too expensive for practical workflows. In this paper, we argue that a sampling-based embedding approach can circumvent these problems. We show that hyperparameters must be chosen carefully, depending on the sampling rate and the intended final embedding. Further, we show how this approach speeds up the computation and increases the quality of the embeddings.

Parametrizing Product Shape Manifolds by Composite Networks

Parametrizations of data manifolds in shape spaces can be computed using the rich toolbox of Riemannian geometry. This, however, often comes with high computational costs, which raises the question if one can learn an efficient neural network approximation. We show that this is indeed possible for shape spaces with a special product structure, namely those smoothly approximable by a direct sum of low-dimensional manifolds. Our proposed architecture leverages this structure by separately learning approximations for the low-dimensional factors and a subsequent combination. After developing the approach as a general framework, we apply it to a shape space of triangular surfaces. Here, typical examples of data manifolds are given through datasets of articulated models and can be factorized, for example, by a Sparse Principal Geodesic Analysis (SPGA). We demonstrate the effectiveness of our proposed approach with experiments on synthetic data as well as manifolds extracted from data via SPGA.

Deep vanishing point detection: Geometric priors make dataset variations vanish

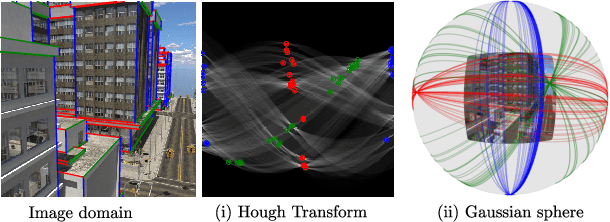
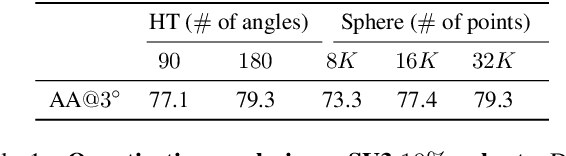
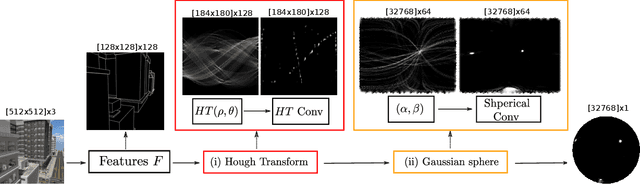
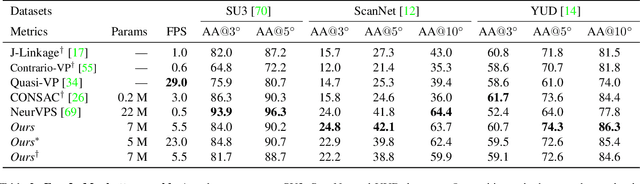
Deep learning has improved vanishing point detection in images. Yet, deep networks require expensive annotated datasets trained on costly hardware and do not generalize to even slightly different domains, and minor problem variants. Here, we address these issues by injecting deep vanishing point detection networks with prior knowledge. This prior knowledge no longer needs to be learned from data, saving valuable annotation efforts and compute, unlocking realistic few-sample scenarios, and reducing the impact of domain changes. Moreover, the interpretability of the priors allows to adapt deep networks to minor problem variations such as switching between Manhattan and non-Manhattan worlds. We seamlessly incorporate two geometric priors: (i) Hough Transform -- mapping image pixels to straight lines, and (ii) Gaussian sphere -- mapping lines to great circles whose intersections denote vanishing points. Experimentally, we ablate our choices and show comparable accuracy to existing models in the large-data setting. We validate our model's improved data efficiency, robustness to domain changes, adaptability to non-Manhattan settings.

DeltaConv: Anisotropic Point Cloud Learning with Exterior Calculus

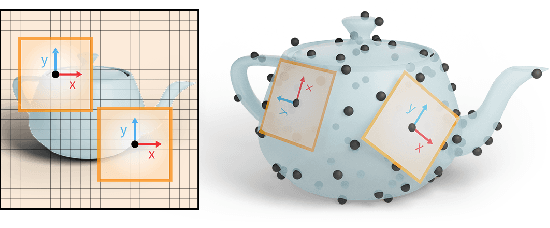
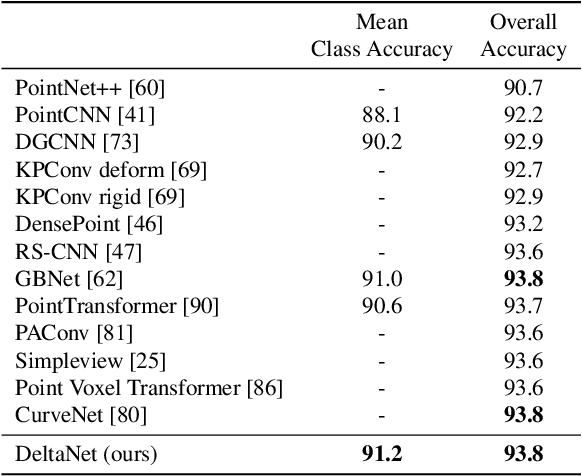
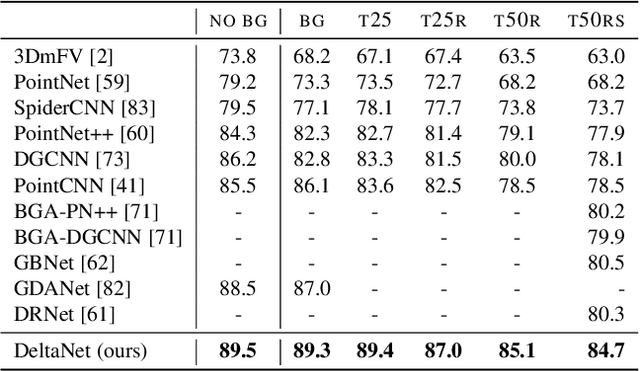
Learning from 3D point-cloud data has rapidly gained momentum, motivated by the success of deep learning on images and the increased availability of 3D data. In this paper, we aim to construct anisotropic convolutions that work directly on the surface derived from a point cloud. This is challenging because of the lack of a global coordinate system for tangential directions on surfaces. We introduce a new convolution operator called DeltaConv, which combines geometric operators from exterior calculus to enable the construction of anisotropic filters on point clouds. Because these operators are defined on scalar- and vector-fields, we separate the network into a scalar- and a vector-stream, which are connected by the operators. The vector stream enables the network to explicitly represent, evaluate, and process directional information. Our convolutions are robust and simple to implement and show improved accuracy compared to state-of-the-art approaches on several benchmarks, while also speeding up training and inference.

Comparing Bayesian Models for Organ Contouring in Headand Neck Radiotherapy

Deep learning models for organ contouring in radiotherapy are poised for clinical usage, but currently, there exist few tools for automated quality assessment (QA) of the predicted contours. Using Bayesian models and their associated uncertainty, one can potentially automate the process of detecting inaccurate predictions. We investigate two Bayesian models for auto-contouring, DropOut and FlipOut, using a quantitative measure - expected calibration error (ECE) and a qualitative measure - region-based accuracy-vs-uncertainty (R-AvU) graphs. It is well understood that a model should have low ECE to be considered trustworthy. However, in a QA context, a model should also have high uncertainty in inaccurate regions and low uncertainty in accurate regions. Such behaviour could direct visual attention of expert users to potentially inaccurate regions, leading to a speed up in the QA process. Using R-AvU graphs, we qualitatively compare the behaviour of different models in accurate and inaccurate regions. Experiments are conducted on the MICCAI2015 Head and Neck Segmentation Challenge and on the DeepMindTCIA CT dataset using three models: DropOut-DICE, Dropout-CE (Cross Entropy) and FlipOut-CE. Quantitative results show that DropOut-DICE has the highest ECE, while Dropout-CE and FlipOut-CE have the lowest ECE. To better understand the difference between DropOut-CE and FlipOut-CE, we use the R-AvU graph which shows that FlipOut-CE has better uncertainty coverage in inaccurate regions than DropOut-CE. Such a combination of quantitative and qualitative metrics explores a new approach that helps to select which model can be deployed as a QA tool in clinical settings.

CNNs on Surfaces using Rotation-Equivariant Features

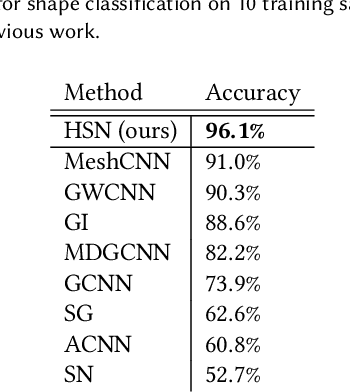
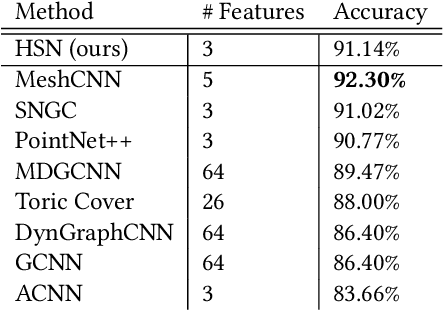
This paper is concerned with a fundamental problem in geometric deep learning that arises in the construction of convolutional neural networks on surfaces. Due to curvature, the transport of filter kernels on surfaces results in a rotational ambiguity, which prevents a uniform alignment of these kernels on the surface. We propose a network architecture for surfaces that consists of vector-valued, rotation-equivariant features. The equivariance property makes it possible to locally align features, which were computed in arbitrary coordinate systems, when aggregating features in a convolution layer. The resulting network is agnostic to the choices of coordinate systems for the tangent spaces on the surface. We implement our approach for triangle meshes. Based on circular harmonic functions, we introduce convolution filters for meshes that are rotation-equivariant at the discrete level. We evaluate the resulting networks on shape correspondence and shape classifications tasks and compare their performance to other approaches.