Improving Uncertainty-Error Correspondence in Deep Bayesian Medical Image Segmentation

Increased usage of automated tools like deep learning in medical image segmentation has alleviated the bottleneck of manual contouring. This has shifted manual labour to quality assessment (QA) of automated contours which involves detecting errors and correcting them. A potential solution to semi-automated QA is to use deep Bayesian uncertainty to recommend potentially erroneous regions, thus reducing time spent on error detection. Previous work has investigated the correspondence between uncertainty and error, however, no work has been done on improving the "utility" of Bayesian uncertainty maps such that it is only present in inaccurate regions and not in the accurate ones. Our work trains the FlipOut model with the Accuracy-vs-Uncertainty (AvU) loss which promotes uncertainty to be present only in inaccurate regions. We apply this method on datasets of two radiotherapy body sites, c.f. head-and-neck CT and prostate MR scans. Uncertainty heatmaps (i.e. predictive entropy) are evaluated against voxel inaccuracies using Receiver Operating Characteristic (ROC) and Precision-Recall (PR) curves. Numerical results show that when compared to the Bayesian baseline the proposed method successfully suppresses uncertainty for accurate voxels, with similar presence of uncertainty for inaccurate voxels. Code to reproduce experiments is available at https://github.com/prerakmody/bayesuncertainty-error-correspondence

Accelerating hyperbolic t-SNE

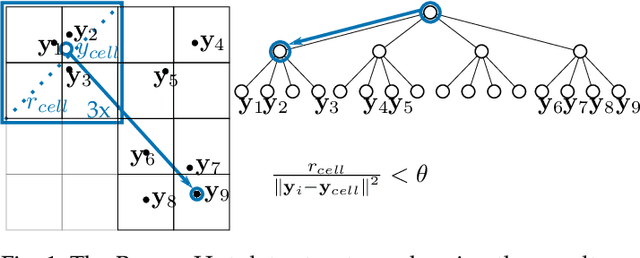
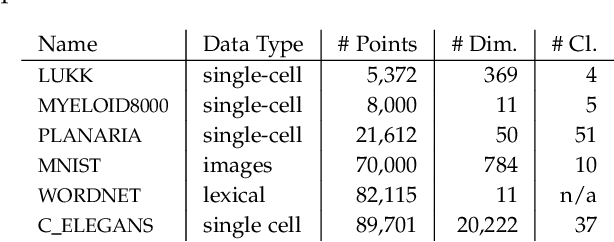
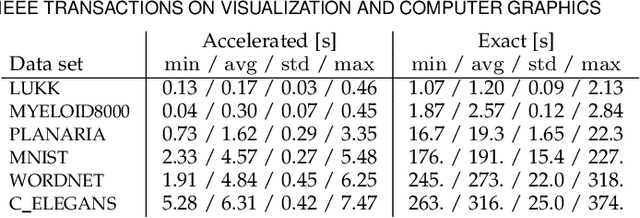
The need to understand the structure of hierarchical or high-dimensional data is present in a variety of fields. Hyperbolic spaces have proven to be an important tool for embedding computations and analysis tasks as their non-linear nature lends itself well to tree or graph data. Subsequently, they have also been used in the visualization of high-dimensional data, where they exhibit increased embedding performance. However, none of the existing dimensionality reduction methods for embedding into hyperbolic spaces scale well with the size of the input data. That is because the embeddings are computed via iterative optimization schemes and the computation cost of every iteration is quadratic in the size of the input. Furthermore, due to the non-linear nature of hyperbolic spaces, Euclidean acceleration structures cannot directly be translated to the hyperbolic setting. This paper introduces the first acceleration structure for hyperbolic embeddings, building upon a polar quadtree. We compare our approach with existing methods and demonstrate that it computes embeddings of similar quality in significantly less time. Implementation and scripts for the experiments can be found at https://graphics.tudelft.nl/accelerating-hyperbolic-tsne.