Accelerating hyperbolic t-SNE

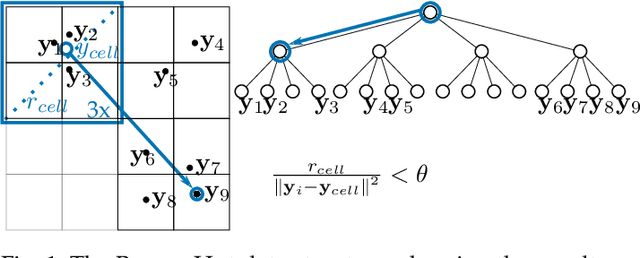
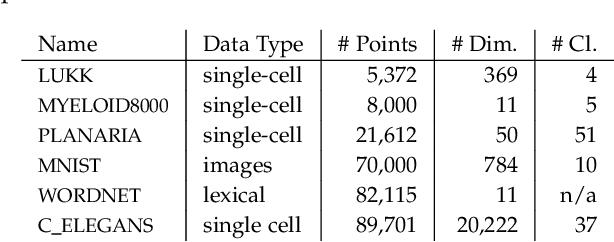
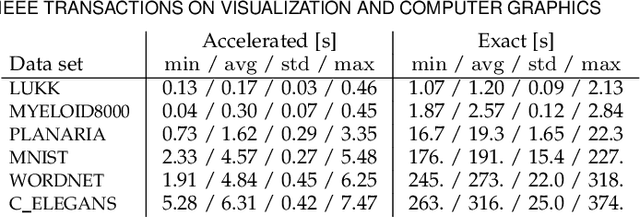
The need to understand the structure of hierarchical or high-dimensional data is present in a variety of fields. Hyperbolic spaces have proven to be an important tool for embedding computations and analysis tasks as their non-linear nature lends itself well to tree or graph data. Subsequently, they have also been used in the visualization of high-dimensional data, where they exhibit increased embedding performance. However, none of the existing dimensionality reduction methods for embedding into hyperbolic spaces scale well with the size of the input data. That is because the embeddings are computed via iterative optimization schemes and the computation cost of every iteration is quadratic in the size of the input. Furthermore, due to the non-linear nature of hyperbolic spaces, Euclidean acceleration structures cannot directly be translated to the hyperbolic setting. This paper introduces the first acceleration structure for hyperbolic embeddings, building upon a polar quadtree. We compare our approach with existing methods and demonstrate that it computes embeddings of similar quality in significantly less time. Implementation and scripts for the experiments can be found at https://graphics.tudelft.nl/accelerating-hyperbolic-tsne.