Accelerating hyperbolic t-SNE

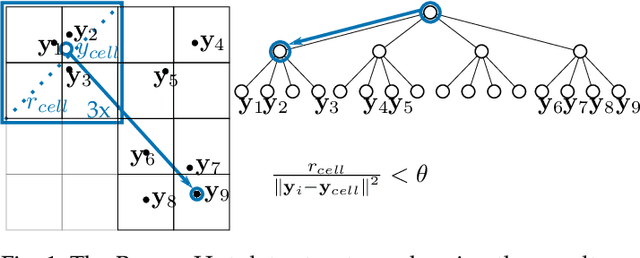
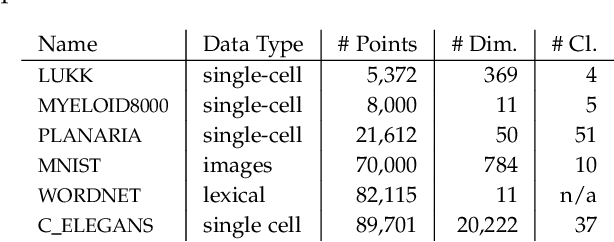
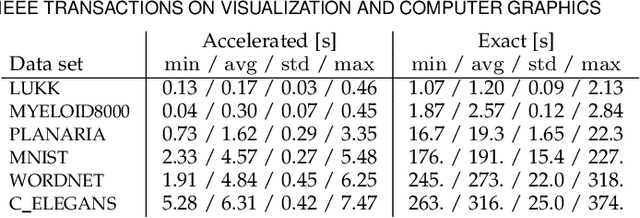
The need to understand the structure of hierarchical or high-dimensional data is present in a variety of fields. Hyperbolic spaces have proven to be an important tool for embedding computations and analysis tasks as their non-linear nature lends itself well to tree or graph data. Subsequently, they have also been used in the visualization of high-dimensional data, where they exhibit increased embedding performance. However, none of the existing dimensionality reduction methods for embedding into hyperbolic spaces scale well with the size of the input data. That is because the embeddings are computed via iterative optimization schemes and the computation cost of every iteration is quadratic in the size of the input. Furthermore, due to the non-linear nature of hyperbolic spaces, Euclidean acceleration structures cannot directly be translated to the hyperbolic setting. This paper introduces the first acceleration structure for hyperbolic embeddings, building upon a polar quadtree. We compare our approach with existing methods and demonstrate that it computes embeddings of similar quality in significantly less time. Implementation and scripts for the experiments can be found at https://graphics.tudelft.nl/accelerating-hyperbolic-tsne.

Tuning the perplexity for and computing sampling-based t-SNE embeddings

Widely used pipelines for the analysis of high-dimensional data utilize two-dimensional visualizations. These are created, e.g., via t-distributed stochastic neighbor embedding (t-SNE). When it comes to large data sets, applying these visualization techniques creates suboptimal embeddings, as the hyperparameters are not suitable for large data. Cranking up these parameters usually does not work as the computations become too expensive for practical workflows. In this paper, we argue that a sampling-based embedding approach can circumvent these problems. We show that hyperparameters must be chosen carefully, depending on the sampling rate and the intended final embedding. Further, we show how this approach speeds up the computation and increases the quality of the embeddings.

Surface Denoising based on Normal Filtering in a Robust Statistics Framework

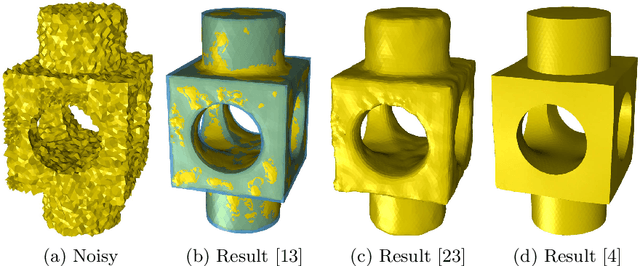
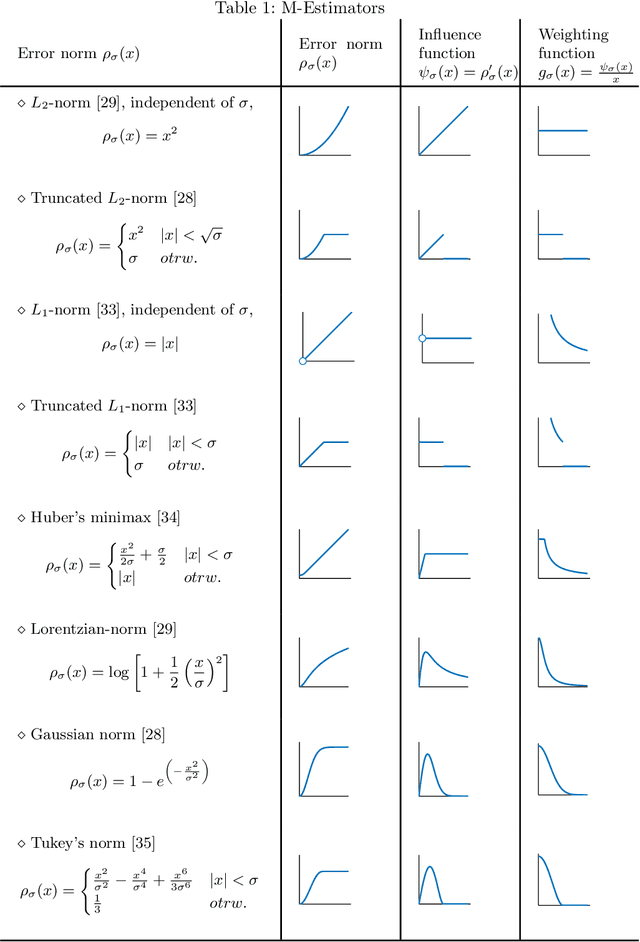
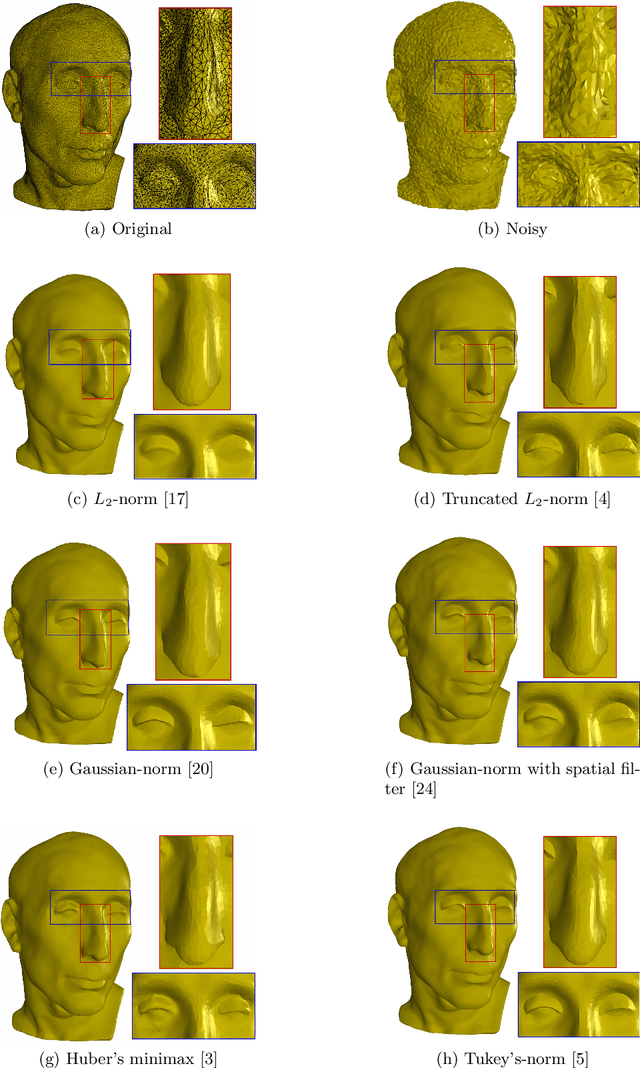
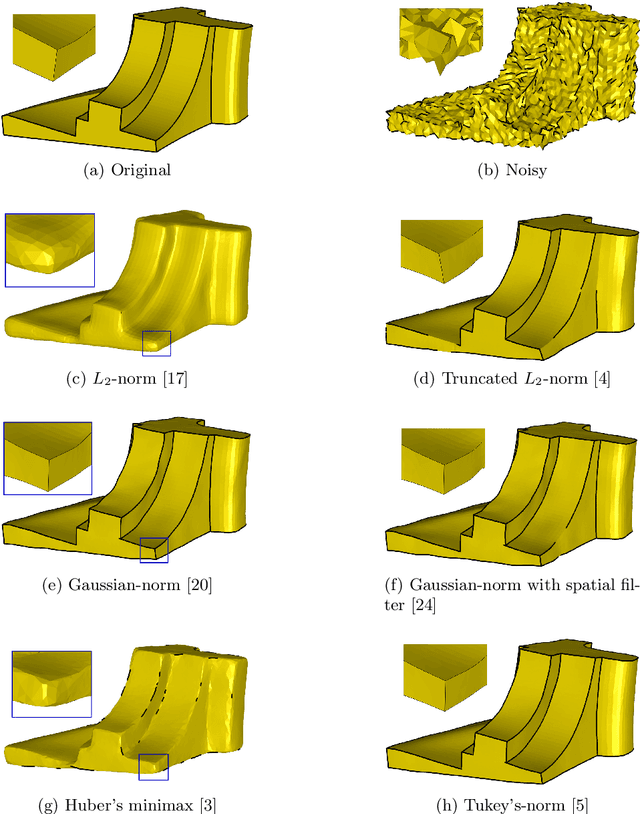
During a surface acquisition process using 3D scanners, noise is inevitable and an important step in geometry processing is to remove these noise components from these surfaces (given as points-set or triangulated mesh). The noise-removal process (denoising) can be performed by filtering the surface normals first and by adjusting the vertex positions according to filtered normals afterwards. Therefore, in many available denoising algorithms, the computation of noise-free normals is a key factor. A variety of filters have been introduced for noise-removal from normals, with different focus points like robustness against outliers or large amplitude of noise. Although these filters are performing well in different aspects, a unified framework is missing to establish the relation between them and to provide a theoretical analysis beyond the performance of each method. In this paper, we introduce such a framework to establish relations between a number of widely-used nonlinear filters for face normals in mesh denoising and vertex normals in point set denoising. We cover robust statistical estimation with M-smoothers and their application to linear and non-linear normal filtering. Although these methods originate in different mathematical theories - which include diffusion-, bilateral-, and directional curvature-based algorithms - we demonstrate that all of them can be cast into a unified framework of robust statistics using robust error norms and their corresponding influence functions. This unification contributes to a better understanding of the individual methods and their relations with each other. Furthermore, the presented framework provides a platform for new techniques to combine the advantages of known filters and to compare them with available methods.