Sub--Riemannian boundary value problems for Optimal Geometric Locomotion

We propose a geometric model for optimal shape-change-induced motions of slender locomotors, e.g., snakes slithering on sand. In these scenarios, the motion of a body in world coordinates is completely determined by the sequence of shapes it assumes. Specifically, we formulate Lagrangian least-dissipation principles as boundary value problems whose solutions are given by sub-Riemannian geodesics. Notably, our geometric model accounts not only for the energy dissipated by the body's displacement through the environment, but also for the energy dissipated by the animal's metabolism or a robot's actuators to induce shape changes such as bending and stretching, thus capturing overall locomotion efficiency. Our continuous model, together with a consistent time and space discretization, enables numerical computation of sub-Riemannian geodesics for three different types of boundary conditions, i.e., fixing initial and target body, restricting to cyclic motion, or solely prescribing body displacement and orientation. The resulting optimal deformation gaits qualitatively match observed motion trajectories of organisms such as snakes and spermatozoa, as well as known optimality results for low-dimensional systems such as Purcell's swimmers. Moreover, being geometrically less rigid than previous frameworks, our model enables new insights into locomotion mechanisms of, e.g., generalized Purcell's swimmers. The code is publicly available.

Geodesic Calculus on Latent Spaces

Latent manifolds of autoencoders provide low-dimensional representations of data, which can be studied from a geometric perspective. We propose to describe these latent manifolds as implicit submanifolds of some ambient latent space. Based on this, we develop tools for a discrete Riemannian calculus approximating classical geometric operators. These tools are robust against inaccuracies of the implicit representation often occurring in practical examples. To obtain a suitable implicit representation, we propose to learn an approximate projection onto the latent manifold by minimizing a denoising objective. This approach is independent of the underlying autoencoder and supports the use of different Riemannian geometries on the latent manifolds. The framework in particular enables the computation of geodesic paths connecting given end points and shooting geodesics via the Riemannian exponential maps on latent manifolds. We evaluate our approach on various autoencoders trained on synthetic and real data.

SDFs from Unoriented Point Clouds using Neural Variational Heat Distances

We propose a novel variational approach for computing neural Signed Distance Fields (SDF) from unoriented point clouds. To this end, we replace the commonly used eikonal equation with the heat method, carrying over to the neural domain what has long been standard practice for computing distances on discrete surfaces. This yields two convex optimization problems for whose solution we employ neural networks: We first compute a neural approximation of the gradients of the unsigned distance field through a small time step of heat flow with weighted point cloud densities as initial data. Then we use it to compute a neural approximation of the SDF. We prove that the underlying variational problems are well-posed. Through numerical experiments, we demonstrate that our method provides state-of-the-art surface reconstruction and consistent SDF gradients. Furthermore, we show in a proof-of-concept that it is accurate enough for solving a PDE on the zero-level set.

Parametrizing Product Shape Manifolds by Composite Networks

Parametrizations of data manifolds in shape spaces can be computed using the rich toolbox of Riemannian geometry. This, however, often comes with high computational costs, which raises the question if one can learn an efficient neural network approximation. We show that this is indeed possible for shape spaces with a special product structure, namely those smoothly approximable by a direct sum of low-dimensional manifolds. Our proposed architecture leverages this structure by separately learning approximations for the low-dimensional factors and a subsequent combination. After developing the approach as a general framework, we apply it to a shape space of triangular surfaces. Here, typical examples of data manifolds are given through datasets of articulated models and can be factorized, for example, by a Sparse Principal Geodesic Analysis (SPGA). We demonstrate the effectiveness of our proposed approach with experiments on synthetic data as well as manifolds extracted from data via SPGA.

Learning Low Bending and Low Distortion Manifold Embeddings: Theory and Applications

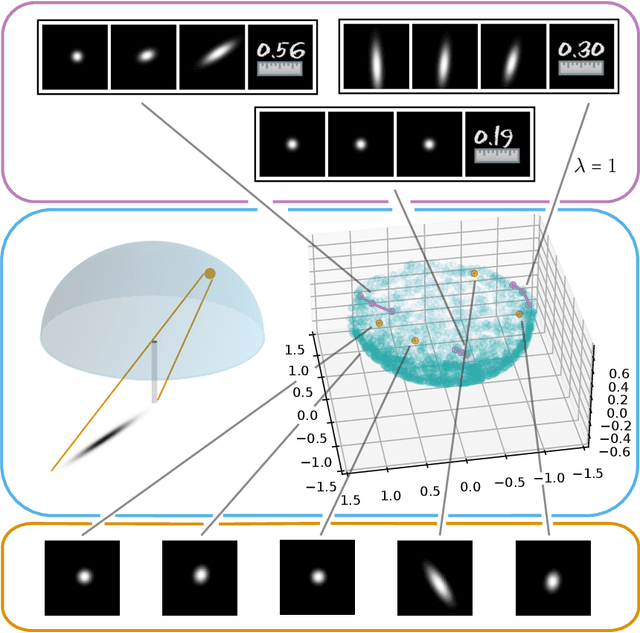
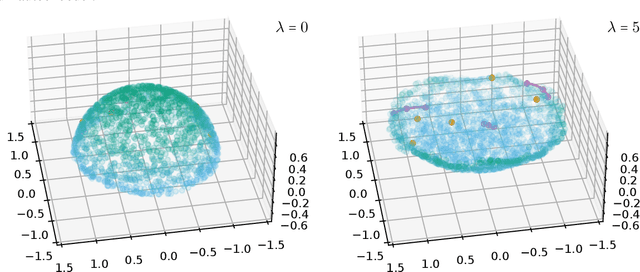
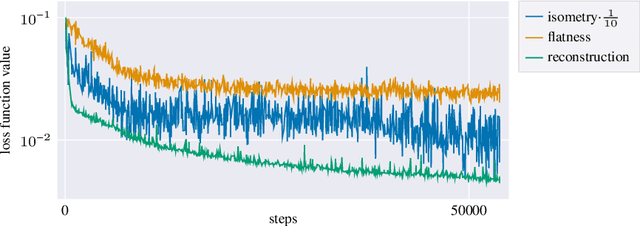
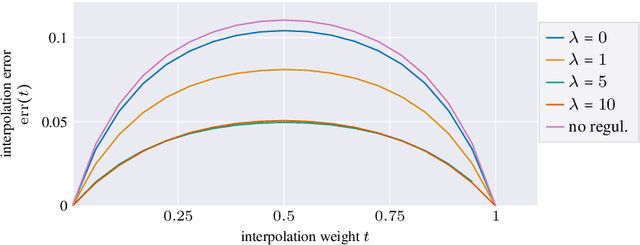
Autoencoders, which consist of an encoder and a decoder, are widely used in machine learning for dimension reduction of high-dimensional data. The encoder embeds the input data manifold into a lower-dimensional latent space, while the decoder represents the inverse map, providing a parametrization of the data manifold by the manifold in latent space. A good regularity and structure of the embedded manifold may substantially simplify further data processing tasks such as cluster analysis or data interpolation. We propose and analyze a novel regularization for learning the encoder component of an autoencoder: a loss functional that prefers isometric, extrinsically flat embeddings and allows to train the encoder on its own. To perform the training it is assumed that for pairs of nearby points on the input manifold their local Riemannian distance and their local Riemannian average can be evaluated. The loss functional is computed via Monte Carlo integration with different sampling strategies for pairs of points on the input manifold. Our main theorem identifies a geometric loss functional of the embedding map as the $\Gamma$-limit of the sampling-dependent loss functionals. Numerical tests, using image data that encodes different explicitly given data manifolds, show that smooth manifold embeddings into latent space are obtained. Due to the promotion of extrinsic flatness, these embeddings are regular enough such that interpolation between not too distant points on the manifold is well approximated by linear interpolation in latent space as one possible postprocessing.

Learning low bending and low distortion manifold embeddings

Autoencoders are a widespread tool in machine learning to transform high-dimensional data into a lowerdimensional representation which still exhibits the essential characteristics of the input. The encoder provides an embedding from the input data manifold into a latent space which may then be used for further processing. For instance, learning interpolation on the manifold may be simplified via the new manifold representation in latent space. The efficiency of such further processing heavily depends on the regularity and structure of the embedding. In this article, the embedding into latent space is regularized via a loss function that promotes an as isometric and as flat embedding as possible. The required training data comprises pairs of nearby points on the input manifold together with their local distance and their local Frechet average. This regularity loss functional even allows to train the encoder on its own. The loss functional is computed via a Monte Carlo integration which is shown to be consistent with a geometric loss functional defined directly on the embedding map. Numerical tests are performed using image data that encodes different data manifolds. The results show that smooth manifold embeddings in latent space are obtained. These embeddings are regular enough such that interpolation between not too distant points on the manifold is well approximated by linear interpolation in latent space.

Cortical Surface Co-Registration based on MRI Images and Photos

Brain shift, i.e. the change in configuration of the brain after opening the dura mater, is a key problem in neuronavigation. We present an approach to co-register intra-operative microscope images with pre-operative MRI to adapt and optimize intra-operative neuronavigation. The tools are a robust classification of sulci on MRI extracted cortical surfaces, guided user marking of most prominent sulci on a microscope image, and the actual variational registration method with a fidelity energy for 3D deformations of the cortical surface combined with a higher order, linear elastica type prior energy. Furthermore, the actual registration is validated on an artificial testbed with known ground truth deformation and on real data of a neuro clinical patient.

Discrete geodesic calculus in the space of viscous fluidic objects

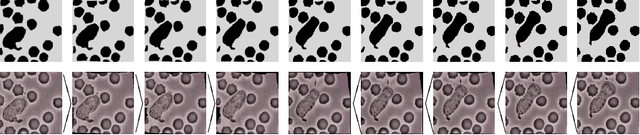
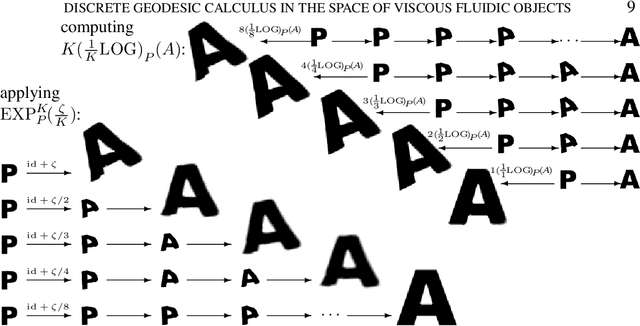
Based on a local approximation of the Riemannian distance on a manifold by a computationally cheap dissimilarity measure, a time discrete geodesic calculus is developed, and applications to shape space are explored. The dissimilarity measure is derived from a deformation energy whose Hessian reproduces the underlying Riemannian metric, and it is used to define length and energy of discrete paths in shape space. The notion of discrete geodesics defined as energy minimizing paths gives rise to a discrete logarithmic map, a variational definition of a discrete exponential map, and a time discrete parallel transport. This new concept is applied to a shape space in which shapes are considered as boundary contours of physical objects consisting of viscous material. The flexibility and computational efficiency of the approach is demonstrated for topology preserving shape morphing, the representation of paths in shape space via local shape variations as path generators, shape extrapolation via discrete geodesic flow, and the transfer of geometric features.