Why the noise model matters: A performance gap in learned regularization

This article addresses the challenge of learning effective regularizers for linear inverse problems. We analyze and compare several types of learned variational regularization against the theoretical benchmark of the optimal affine reconstruction, i.e. the best possible affine linear map for minimizing the mean squared error. It is known that this optimal reconstruction can be achieved using Tikhonov regularization, but this requires precise knowledge of the noise covariance to properly weight the data fidelity term. However, in many practical applications, noise statistics are unknown. We therefore investigate the performance of regularization methods learned without access to this noise information, focusing on Tikhonov, Lavrentiev, and quadratic regularization. Our theoretical analysis and numerical experiments demonstrate that for non-white noise, a performance gap emerges between these methods and the optimal affine reconstruction. Furthermore, we show that these different types of regularization yield distinct results, highlighting that the choice of regularizer structure is critical when the noise model is not explicitly learned. Our findings underscore the significant value of accurately modeling or co-learning noise statistics in data-driven regularization.

Primal-dual residual networks

In this work, we propose a deep neural network architecture motivated by primal-dual splitting methods from convex optimization. We show theoretically that there exists a close relation between the derived architecture and residual networks, and further investigate this connection in numerical experiments. Moreover, we demonstrate how our approach can be used to unroll optimization algorithms for certain problems with hard constraints. Using the example of speech dequantization, we show that our method can outperform classical splitting methods when both are applied to the same task.

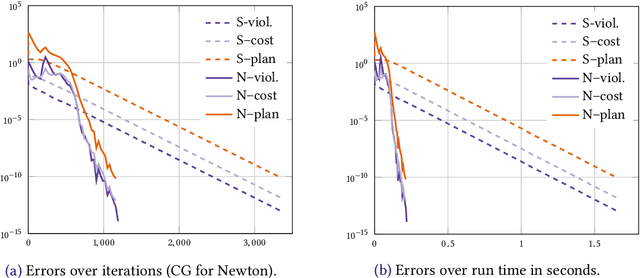
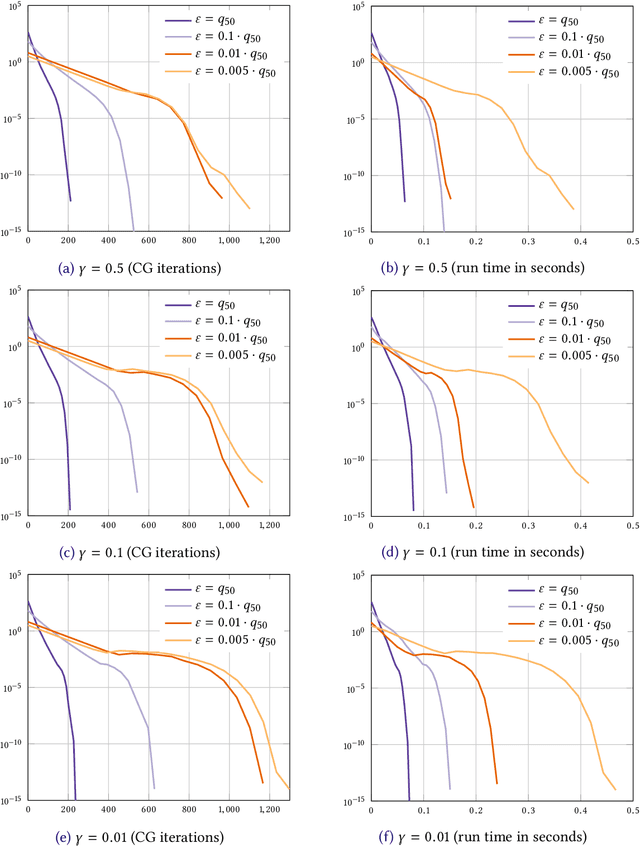
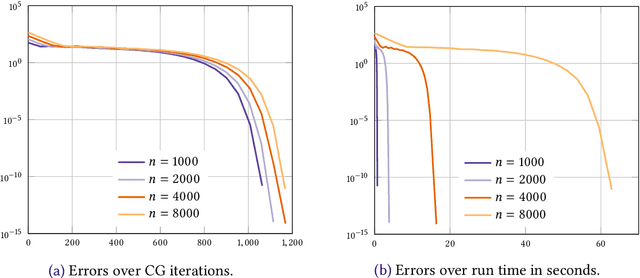
A Sinkhorn-Newton method for entropic optimal transport

We consider the entropic regularization of discretized optimal transport and propose to solve its optimality conditions via a logarithmic Newton iteration. We show a quadratic convergence rate and validate numerically that the method compares favorably with the more commonly used Sinkhorn--Knopp algorithm for small regularization strength. We further investigate numerically the robustness of the proposed method with respect to parameters such as the mesh size of the discretization.