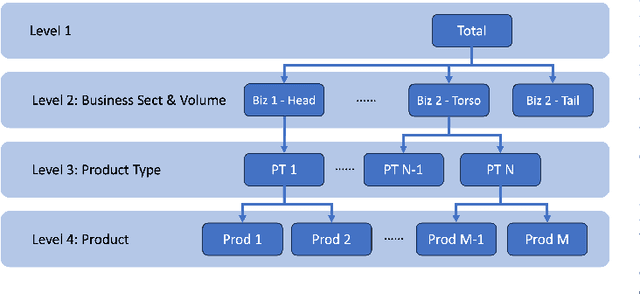
A Comprehensive Forecasting Framework based on Multi-Stage Hierarchical Forecasting Reconciliation and Adjustment

Ads demand forecasting for Walmart's ad products plays a critical role in enabling effective resource planning, allocation, and management of ads performance. In this paper, we introduce a comprehensive demand forecasting system that tackles hierarchical time series forecasting in business settings. Though traditional hierarchical reconciliation methods ensure forecasting coherence, they often trade off accuracy for coherence especially at lower levels and fail to capture the seasonality unique to each time-series in the hierarchy. Thus, we propose a novel framework "Multi-Stage Hierarchical Forecasting Reconciliation and Adjustment (Multi-Stage HiFoReAd)" to address the challenges of preserving seasonality, ensuring coherence, and improving accuracy. Our system first utilizes diverse models, ensembled through Bayesian Optimization (BO), achieving base forecasts. The generated base forecasts are then passed into the Multi-Stage HiFoReAd framework. The initial stage refines the hierarchy using Top-Down forecasts and "harmonic alignment." The second stage aligns the higher levels' forecasts using MinTrace algorithm, following which the last two levels undergo "harmonic alignment" and "stratified scaling", to eventually achieve accurate and coherent forecasts across the whole hierarchy. Our experiments on Walmart's internal Ads-demand dataset and 3 other public datasets, each with 4 hierarchical levels, demonstrate that the average Absolute Percentage Error from the cross-validation sets improve from 3% to 40% across levels against BO-ensemble of models (LGBM, MSTL+ETS, Prophet) as well as from 1.2% to 92.9% against State-Of-The-Art models. In addition, the forecasts at all hierarchical levels are proved to be coherent. The proposed framework has been deployed and leveraged by Walmart's ads, sales and operations teams to track future demands, make informed decisions and plan resources.

Graph Sparsifications using Neural Network Assisted Monte Carlo Tree Search

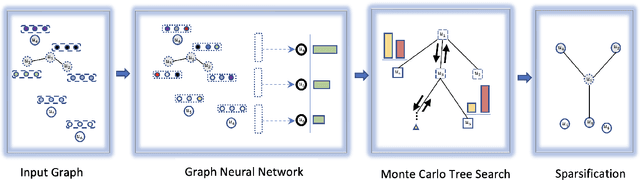
Graph neural networks have been successful for machine learning, as well as for combinatorial and graph problems such as the Subgraph Isomorphism Problem and the Traveling Salesman Problem. We describe an approach for computing graph sparsifiers by combining a graph neural network and Monte Carlo Tree Search. We first train a graph neural network that takes as input a partial solution and proposes a new node to be added as output. This neural network is then used in a Monte Carlo search to compute a sparsifier. The proposed method consistently outperforms several standard approximation algorithms on different types of graphs and often finds the optimal solution.

Nearly Optimal Steiner Trees using Graph Neural Network Assisted Monte Carlo Tree Search

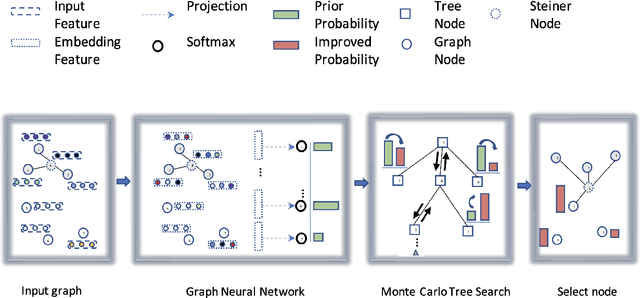
Graph neural networks are useful for learning problems, as well as for combinatorial and graph problems such as the Subgraph Isomorphism Problem and the Traveling Salesman Problem. We describe an approach for computing Steiner Trees by combining a graph neural network and Monte Carlo Tree Search. We first train a graph neural network that takes as input a partial solution and proposes a new node to be added as output. This neural network is then used in a Monte Carlo search to compute a Steiner tree. The proposed method consistently outperforms the standard 2-approximation algorithm on many different types of graphs and often finds the optimal solution.

Computing Steiner Trees using Graph Neural Networks

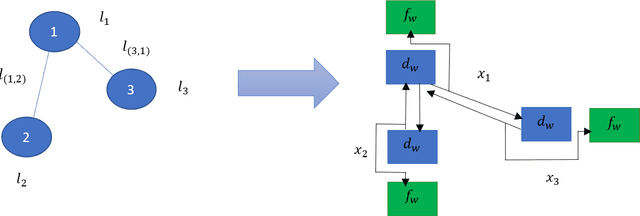
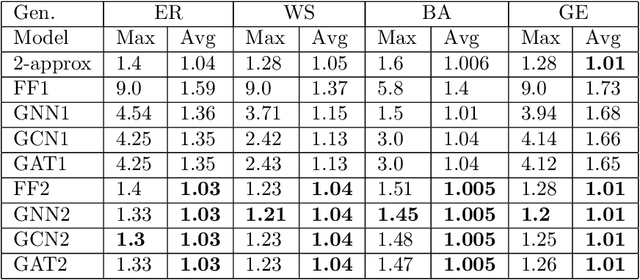
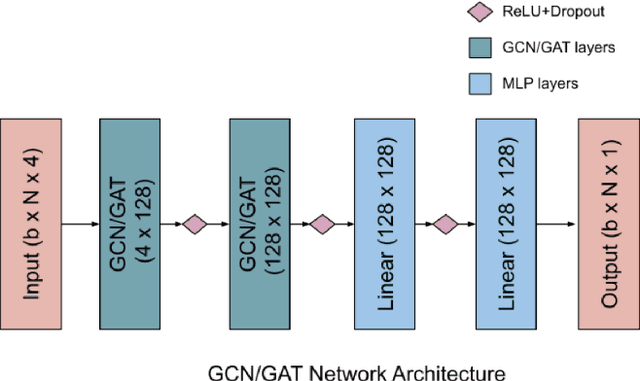
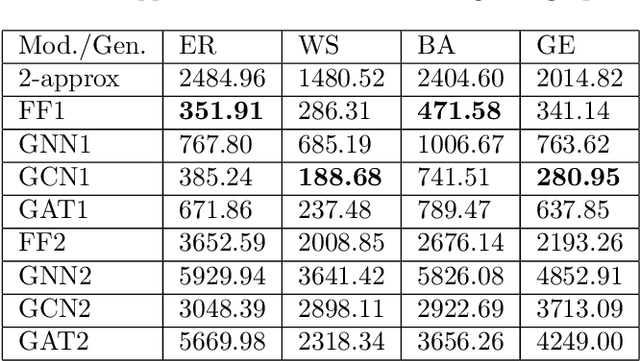
Graph neural networks have been successful in many learning problems and real-world applications. A recent line of research explores the power of graph neural networks to solve combinatorial and graph algorithmic problems such as subgraph isomorphism, detecting cliques, and the traveling salesman problem. However, many NP-complete problems are as of yet unexplored using this method. In this paper, we tackle the Steiner Tree Problem. We employ four learning frameworks to compute low cost Steiner trees: feed-forward neural networks, graph neural networks, graph convolutional networks, and a graph attention model. We use these frameworks in two fundamentally different ways: 1) to train the models to learn the actual Steiner tree nodes, 2) to train the model to learn good Steiner point candidates to be connected to the constructed tree using a shortest path in a greedy fashion. We illustrate the robustness of our heuristics on several random graph generation models as well as the SteinLib data library. Our finding suggests that the out-of-the-box application of GNN methods does worse than the classic 2-approximation method. However, when combined with a greedy shortest path construction, it even does slightly better than the 2-approximation algorithm. This result sheds light on the fundamental capabilities and limitations of graph learning techniques on classical NP-complete problems.

AgentBuddy: A Contextual Bandit based Decision Support System for Customer Support Agents

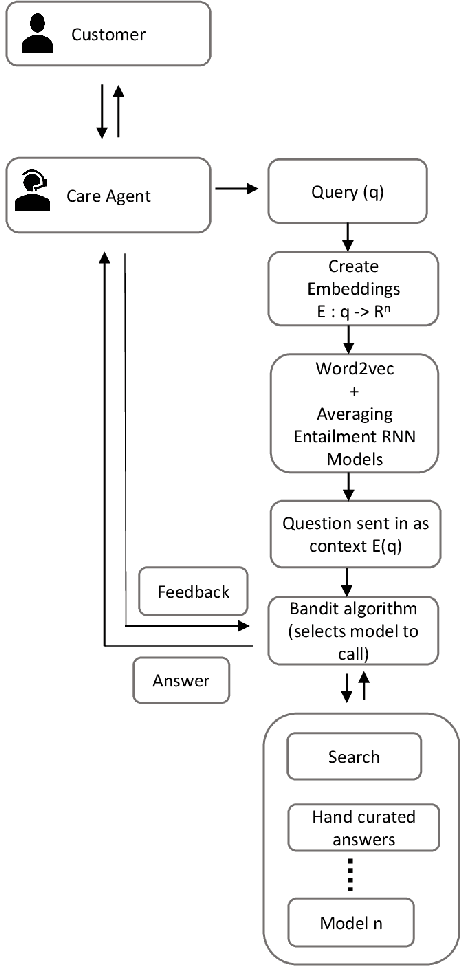
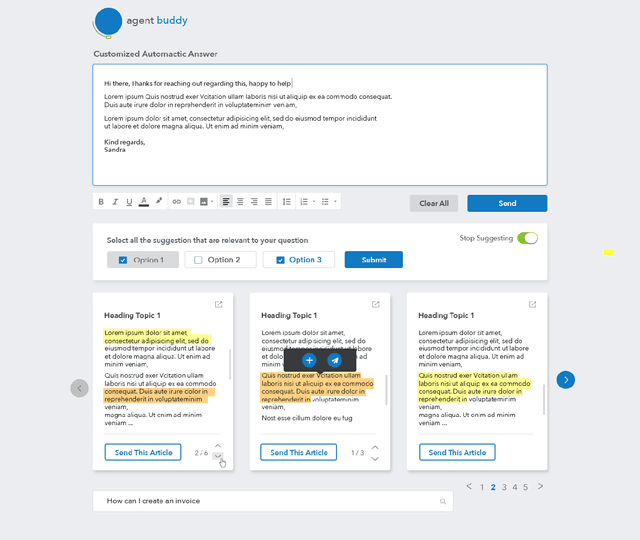
In this short paper, we present early insights from a Decision Support System for Customer Support Agents (CSAs) serving customers of a leading accounting software. The system is under development and is designed to provide suggestions to CSAs to make them more productive. A unique aspect of the solution is the use of bandit algorithms to create a tractable human-in-the-loop system that can learn from CSAs in an online fashion. In addition to discussing the ML aspects, we also bring out important insights we gleaned from early feedback from CSAs. These insights motivate our future work and also might be of wider interest to ML practitioners.