Distributed Training of Large Graph Neural Networks with Variable Communication Rates

Training Graph Neural Networks (GNNs) on large graphs presents unique challenges due to the large memory and computing requirements. Distributed GNN training, where the graph is partitioned across multiple machines, is a common approach to training GNNs on large graphs. However, as the graph cannot generally be decomposed into small non-interacting components, data communication between the training machines quickly limits training speeds. Compressing the communicated node activations by a fixed amount improves the training speeds, but lowers the accuracy of the trained GNN. In this paper, we introduce a variable compression scheme for reducing the communication volume in distributed GNN training without compromising the accuracy of the learned model. Based on our theoretical analysis, we derive a variable compression method that converges to a solution equivalent to the full communication case, for all graph partitioning schemes. Our empirical results show that our method attains a comparable performance to the one obtained with full communication. We outperform full communication at any fixed compression ratio for any communication budget.

DeepGraphDMD: Interpretable Spatio-Temporal Decomposition of Non-linear Functional Brain Network Dynamics

Functional brain dynamics is supported by parallel and overlapping functional network modes that are associated with specific neural circuits. Decomposing these network modes from fMRI data and finding their temporal characteristics is challenging due to their time-varying nature and the non-linearity of the functional dynamics. Dynamic Mode Decomposition (DMD) algorithms have been quite popular for solving this decomposition problem in recent years. In this work, we apply GraphDMD -- an extension of the DMD for network data -- to extract the dynamic network modes and their temporal characteristics from the fMRI time series in an interpretable manner. GraphDMD, however, regards the underlying system as a linear dynamical system that is sub-optimal for extracting the network modes from non-linear functional data. In this work, we develop a generalized version of the GraphDMD algorithm -- DeepGraphDMD -- applicable to arbitrary non-linear graph dynamical systems. DeepGraphDMD is an autoencoder-based deep learning model that learns Koopman eigenfunctions for graph data and embeds the non-linear graph dynamics into a latent linear space. We show the effectiveness of our method in both simulated data and the HCP resting-state fMRI data. In the HCP data, DeepGraphDMD provides novel insights into cognitive brain functions by discovering two major network modes related to fluid and crystallized intelligence.

Computing Steiner Trees using Graph Neural Networks

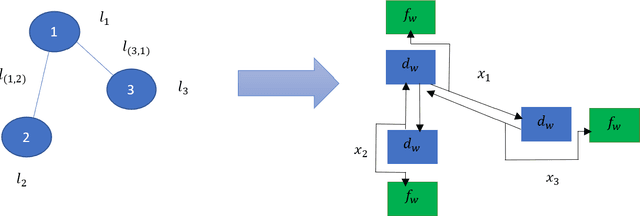
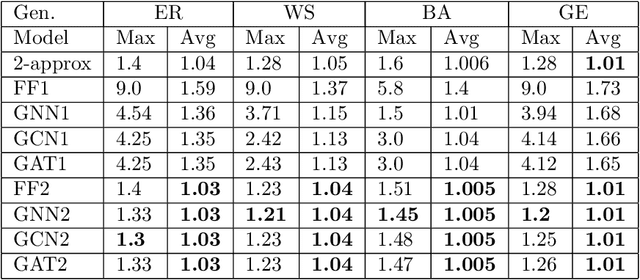
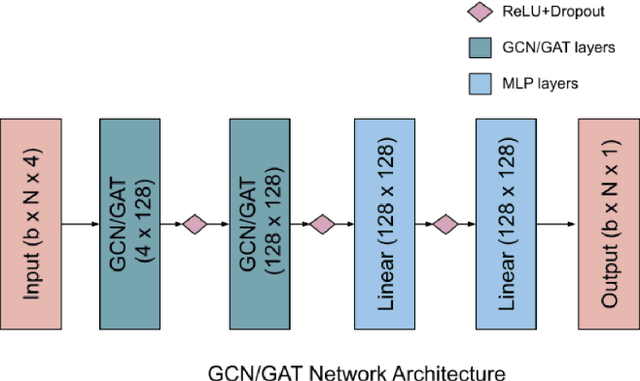
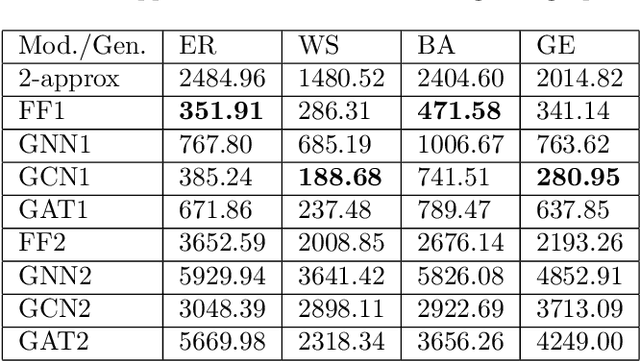
Graph neural networks have been successful in many learning problems and real-world applications. A recent line of research explores the power of graph neural networks to solve combinatorial and graph algorithmic problems such as subgraph isomorphism, detecting cliques, and the traveling salesman problem. However, many NP-complete problems are as of yet unexplored using this method. In this paper, we tackle the Steiner Tree Problem. We employ four learning frameworks to compute low cost Steiner trees: feed-forward neural networks, graph neural networks, graph convolutional networks, and a graph attention model. We use these frameworks in two fundamentally different ways: 1) to train the models to learn the actual Steiner tree nodes, 2) to train the model to learn good Steiner point candidates to be connected to the constructed tree using a shortest path in a greedy fashion. We illustrate the robustness of our heuristics on several random graph generation models as well as the SteinLib data library. Our finding suggests that the out-of-the-box application of GNN methods does worse than the classic 2-approximation method. However, when combined with a greedy shortest path construction, it even does slightly better than the 2-approximation algorithm. This result sheds light on the fundamental capabilities and limitations of graph learning techniques on classical NP-complete problems.