Graph Sparsifications using Neural Network Assisted Monte Carlo Tree Search

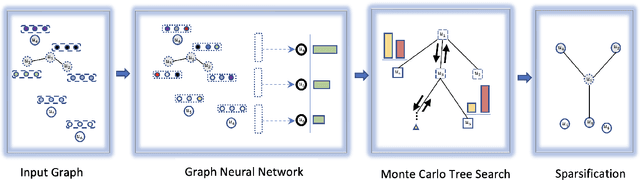
Graph neural networks have been successful for machine learning, as well as for combinatorial and graph problems such as the Subgraph Isomorphism Problem and the Traveling Salesman Problem. We describe an approach for computing graph sparsifiers by combining a graph neural network and Monte Carlo Tree Search. We first train a graph neural network that takes as input a partial solution and proposes a new node to be added as output. This neural network is then used in a Monte Carlo search to compute a sparsifier. The proposed method consistently outperforms several standard approximation algorithms on different types of graphs and often finds the optimal solution.

Nearly Optimal Steiner Trees using Graph Neural Network Assisted Monte Carlo Tree Search

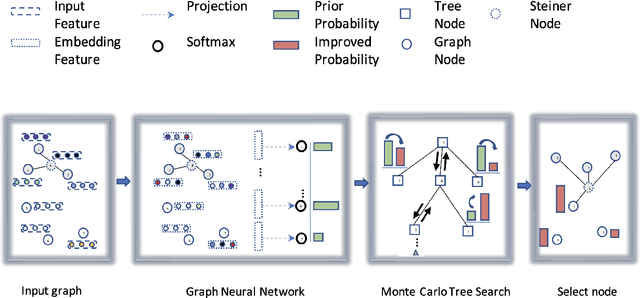
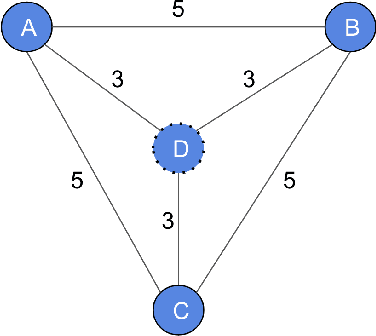
Graph neural networks are useful for learning problems, as well as for combinatorial and graph problems such as the Subgraph Isomorphism Problem and the Traveling Salesman Problem. We describe an approach for computing Steiner Trees by combining a graph neural network and Monte Carlo Tree Search. We first train a graph neural network that takes as input a partial solution and proposes a new node to be added as output. This neural network is then used in a Monte Carlo search to compute a Steiner tree. The proposed method consistently outperforms the standard 2-approximation algorithm on many different types of graphs and often finds the optimal solution.

Computing Steiner Trees using Graph Neural Networks

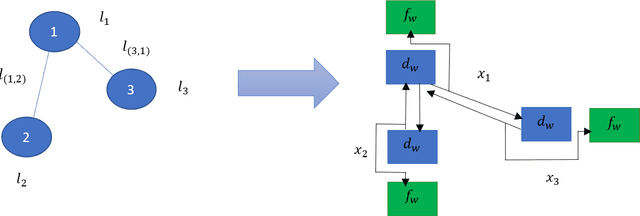
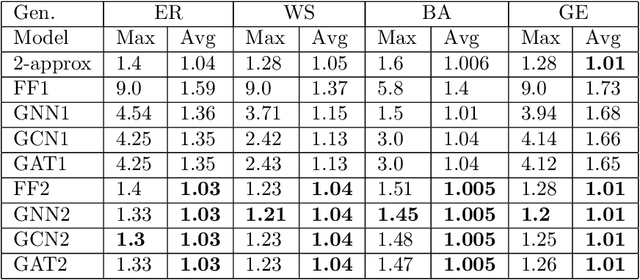
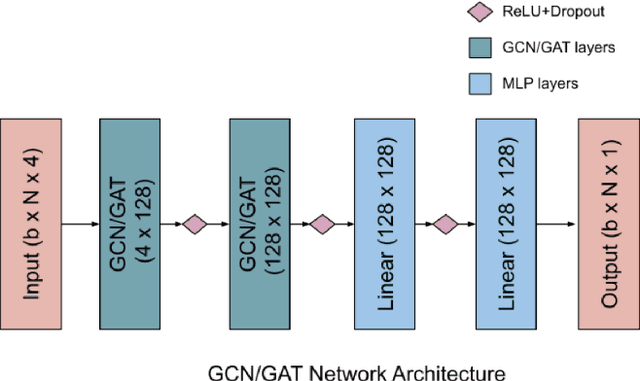
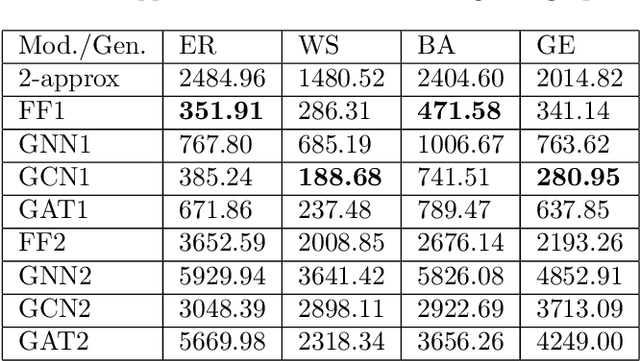
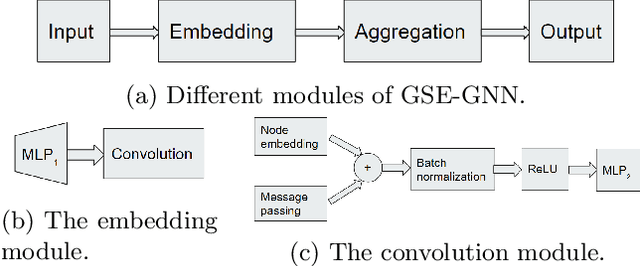
Graph neural networks have been successful in many learning problems and real-world applications. A recent line of research explores the power of graph neural networks to solve combinatorial and graph algorithmic problems such as subgraph isomorphism, detecting cliques, and the traveling salesman problem. However, many NP-complete problems are as of yet unexplored using this method. In this paper, we tackle the Steiner Tree Problem. We employ four learning frameworks to compute low cost Steiner trees: feed-forward neural networks, graph neural networks, graph convolutional networks, and a graph attention model. We use these frameworks in two fundamentally different ways: 1) to train the models to learn the actual Steiner tree nodes, 2) to train the model to learn good Steiner point candidates to be connected to the constructed tree using a shortest path in a greedy fashion. We illustrate the robustness of our heuristics on several random graph generation models as well as the SteinLib data library. Our finding suggests that the out-of-the-box application of GNN methods does worse than the classic 2-approximation method. However, when combined with a greedy shortest path construction, it even does slightly better than the 2-approximation algorithm. This result sheds light on the fundamental capabilities and limitations of graph learning techniques on classical NP-complete problems.

Stress-Plus-X (SPX) Graph Layout

Stress, edge crossings, and crossing angles play an important role in the quality and readability of graph drawings. Most standard graph drawing algorithms optimize one of these criteria which may lead to layouts that are deficient in other criteria. We introduce an optimization framework, Stress-Plus-X (SPX), that simultaneously optimizes stress together with several other criteria: edge crossings, minimum crossing angle, and upwardness (for directed acyclic graphs). SPX achieves results that are close to the state-of-the-art algorithms that optimize these metrics individually. SPX is flexible and extensible and can optimize a subset or all of these criteria simultaneously. Our experimental analysis shows that our joint optimization approach is successful in drawing graphs with good performance across readability criteria.