Persistent Classification: A New Approach to Stability of Data and Adversarial Examples

There are a number of hypotheses underlying the existence of adversarial examples for classification problems. These include the high-dimensionality of the data, high codimension in the ambient space of the data manifolds of interest, and that the structure of machine learning models may encourage classifiers to develop decision boundaries close to data points. This article proposes a new framework for studying adversarial examples that does not depend directly on the distance to the decision boundary. Similarly to the smoothed classifier literature, we define a (natural or adversarial) data point to be $(\gamma,\sigma)$-stable if the probability of the same classification is at least $\gamma$ for points sampled in a Gaussian neighborhood of the point with a given standard deviation $\sigma$. We focus on studying the differences between persistence metrics along interpolants of natural and adversarial points. We show that adversarial examples have significantly lower persistence than natural examples for large neural networks in the context of the MNIST and ImageNet datasets. We connect this lack of persistence with decision boundary geometry by measuring angles of interpolants with respect to decision boundaries. Finally, we connect this approach with robustness by developing a manifold alignment gradient metric and demonstrating the increase in robustness that can be achieved when training with the addition of this metric.

An Exact Kernel Equivalence for Finite Classification Models

We explore the equivalence between neural networks and kernel methods by deriving the first exact representation of any finite-size parametric classification model trained with gradient descent as a kernel machine. We compare our exact representation to the well-known Neural Tangent Kernel (NTK) and discuss approximation error relative to the NTK and other non-exact path kernel formulations. We experimentally demonstrate that the kernel can be computed for realistic networks up to machine precision. We use this exact kernel to show that our theoretical contribution can provide useful insights into the predictions made by neural networks, particularly the way in which they generalize.

SAD: Saliency-based Defenses Against Adversarial Examples

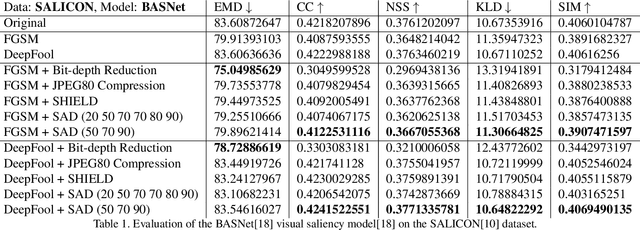
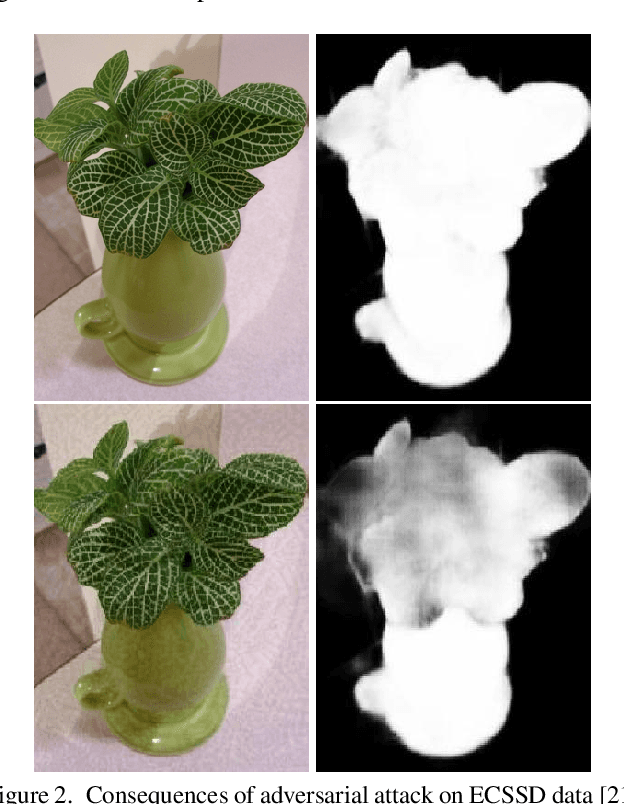
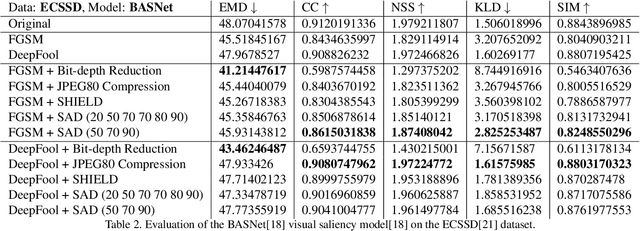
With the rise in popularity of machine and deep learning models, there is an increased focus on their vulnerability to malicious inputs. These adversarial examples drift model predictions away from the original intent of the network and are a growing concern in practical security. In order to combat these attacks, neural networks can leverage traditional image processing approaches or state-of-the-art defensive models to reduce perturbations in the data. Defensive approaches that take a global approach to noise reduction are effective against adversarial attacks, however their lossy approach often distorts important data within the image. In this work, we propose a visual saliency based approach to cleaning data affected by an adversarial attack. Our model leverages the salient regions of an adversarial image in order to provide a targeted countermeasure while comparatively reducing loss within the cleaned images. We measure the accuracy of our model by evaluating the effectiveness of state-of-the-art saliency methods prior to attack, under attack, and after application of cleaning methods. We demonstrate the effectiveness of our proposed approach in comparison with related defenses and against established adversarial attack methods, across two saliency datasets. Our targeted approach shows significant improvements in a range of standard statistical and distance saliency metrics, in comparison with both traditional and state-of-the-art approaches.