Tensor Networks for Language Modeling

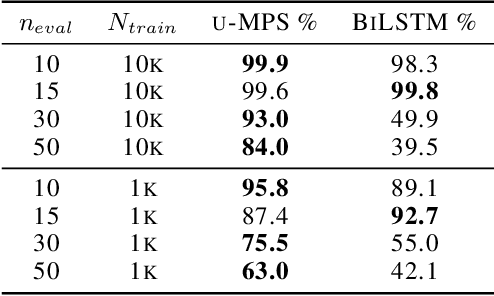
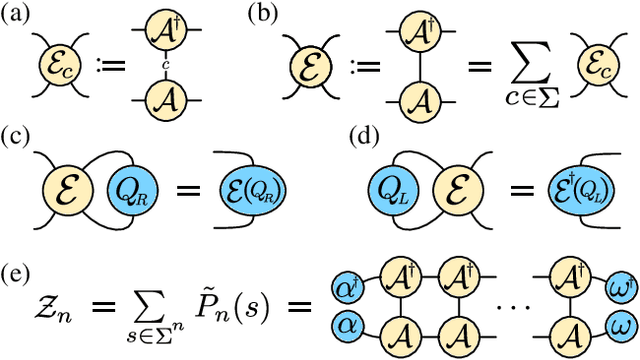
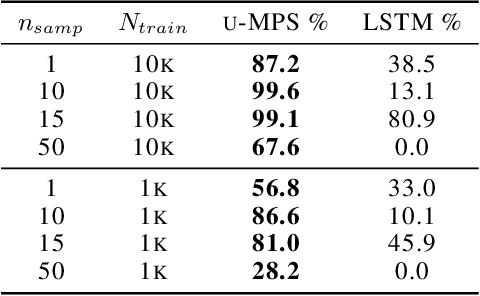
The tensor network formalism has enjoyed over two decades of success in modeling the behavior of complex quantum-mechanical systems, but has only recently and sporadically been leveraged in machine learning. Here we introduce a uniform matrix product state (u-MPS) model for probabilistic modeling of sequence data. We identify several distinctive features of this recurrent generative model, notably the ability to condition or marginalize sampling on characters at arbitrary locations within a sequence, with no need for approximate sampling methods. Despite the sequential architecture of u-MPS, we show that a recursive evaluation algorithm can be used to parallelize its inference and training, with a string of length n only requiring parallel time $\mathcal{O}(\log n)$ to evaluate. Experiments on a context-free language demonstrate a strong capacity to learn grammatical structure from limited data, pointing towards the potential of tensor networks for language modeling applications.