From Language Models over Tokens to Language Models over Characters

Modern language models are internally -- and mathematically -- distributions over token strings rather than \emph{character} strings, posing numerous challenges for programmers building user applications on top of them. For example, if a prompt is specified as a character string, it must be tokenized before passing it to the token-level language model. Thus, the tokenizer and consequent analyses are very sensitive to the specification of the prompt (e.g., if the prompt ends with a space or not). This paper presents algorithms for converting token-level language models to character-level ones. We present both exact and approximate algorithms. In the empirical portion of the paper, we benchmark the practical runtime and approximation quality. We find that -- even with a small computation budget -- our method is able to accurately approximate the character-level distribution (less than 0.00021 excess bits / character) at reasonably fast speeds (46.3 characters / second) on the Llama 3.1 8B language model.

The Foundations of Tokenization: Statistical and Computational Concerns

Tokenization - the practice of converting strings of characters over an alphabet into sequences of tokens over a vocabulary - is a critical yet under-theorized step in the NLP pipeline. Notably, it remains the only major step not fully integrated into widely used end-to-end neural models. This paper aims to address this theoretical gap by laying the foundations of tokenization from a formal perspective. By articulating and extending basic properties about the category of stochastic maps, we propose a unified framework for representing and analyzing tokenizer models. This framework allows us to establish general conditions for the use of tokenizers. In particular, we formally establish the necessary and sufficient conditions for a tokenizer model to preserve the consistency of statistical estimators. Additionally, we discuss statistical and computational concerns crucial for the design and implementation of tokenizer models. The framework and results advanced in this paper represent a step toward a robust theoretical foundation for neural language modeling.

An enriched category theory of language: from syntax to semantics

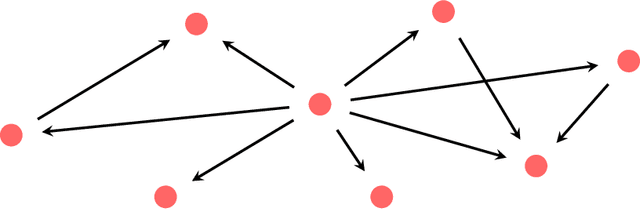
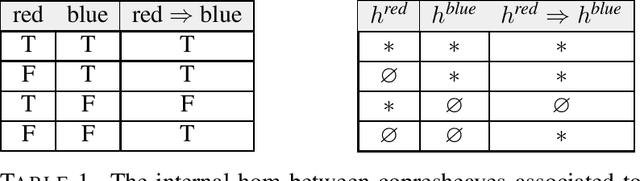
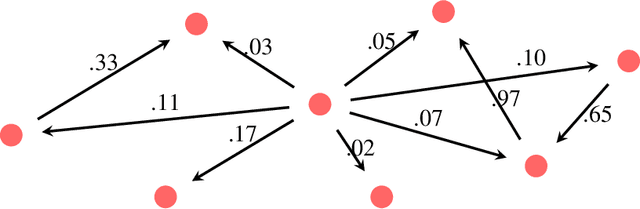
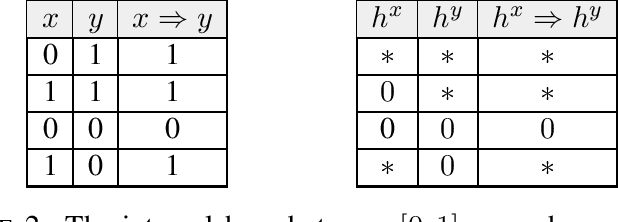
Given a piece of text, the ability to generate a coherent extension of it implies some sophistication, including a knowledge of grammar and semantics. In this paper, we propose a mathematical framework for passing from probability distributions on extensions of given texts to an enriched category containing semantic information. Roughly speaking, we model probability distributions on texts as a category enriched over the unit interval. Objects of this category are expressions in language and hom objects are conditional probabilities that one expression is an extension of another. This category is syntactical: it describes what goes with what. We then pass to the enriched category of unit interval-valued copresheaves on this syntactical category to find semantic information.

Tensor Networks for Language Modeling

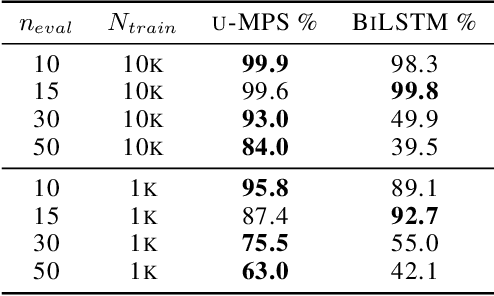
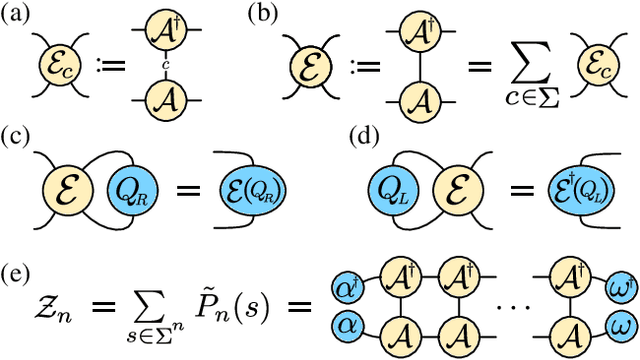
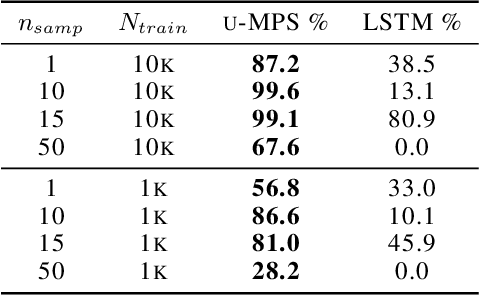
The tensor network formalism has enjoyed over two decades of success in modeling the behavior of complex quantum-mechanical systems, but has only recently and sporadically been leveraged in machine learning. Here we introduce a uniform matrix product state (u-MPS) model for probabilistic modeling of sequence data. We identify several distinctive features of this recurrent generative model, notably the ability to condition or marginalize sampling on characters at arbitrary locations within a sequence, with no need for approximate sampling methods. Despite the sequential architecture of u-MPS, we show that a recursive evaluation algorithm can be used to parallelize its inference and training, with a string of length n only requiring parallel time $\mathcal{O}(\log n)$ to evaluate. Experiments on a context-free language demonstrate a strong capacity to learn grammatical structure from limited data, pointing towards the potential of tensor networks for language modeling applications.

Modeling Sequences with Quantum States: A Look Under the Hood

Classical probability distributions on sets of sequences can be modeled using quantum states. Here, we do so with a quantum state that is pure and entangled. Because it is entangled, the reduced densities that describe subsystems also carry information about the complementary subsystem. This is in contrast to the classical marginal distributions on a subsystem in which information about the complementary system has been integrated out and lost. A training algorithm based on the density matrix renormalization group (DMRG) procedure uses the extra information contained in the reduced densities and organizes it into a tensor network model. An understanding of the extra information contained in the reduced densities allow us to examine the mechanics of this DMRG algorithm and study the generalization error of the resulting model. As an illustration, we work with the even-parity dataset and produce an estimate for the generalization error as a function of the fraction of the dataset used in training.

Probabilistic Modeling with Matrix Product States

Inspired by the possibility that generative models based on quantum circuits can provide a useful inductive bias for sequence modeling tasks, we propose an efficient training algorithm for a subset of classically simulable quantum circuit models. The gradient-free algorithm, presented as a sequence of exactly solvable effective models, is a modification of the density matrix renormalization group procedure adapted for learning a probability distribution. The conclusion that circuit-based models offer a useful inductive bias for classical datasets is supported by experimental results on the parity learning problem.

Language as a matrix product state

We propose a statistical model for natural language that begins by considering language as a monoid, then representing it in complex matrices with a compatible translation invariant probability measure. We interpret the probability measure as arising via the Born rule from a translation invariant matrix product state.