Juan Luis Gastaldi
Language Models over Canonical Byte-Pair Encodings
Jun 09, 2025Abstract:Modern language models represent probability distributions over character strings as distributions over (shorter) token strings derived via a deterministic tokenizer, such as byte-pair encoding. While this approach is highly effective at scaling up language models to large corpora, its current incarnations have a concerning property: the model assigns nonzero probability mass to an exponential number of $\it{noncanonical}$ token encodings of each character string -- these are token strings that decode to valid character strings but are impossible under the deterministic tokenizer (i.e., they will never be seen in any training corpus, no matter how large). This misallocation is both erroneous, as noncanonical strings never appear in training data, and wasteful, diverting probability mass away from plausible outputs. These are avoidable mistakes! In this work, we propose methods to enforce canonicality in token-level language models, ensuring that only canonical token strings are assigned positive probability. We present two approaches: (1) canonicality by conditioning, leveraging test-time inference strategies without additional training, and (2) canonicality by construction, a model parameterization that guarantees canonical outputs but requires training. We demonstrate that fixing canonicality mistakes improves the likelihood of held-out data for several models and corpora.
From Language Models over Tokens to Language Models over Characters
Dec 04, 2024Abstract:Modern language models are internally -- and mathematically -- distributions over token strings rather than \emph{character} strings, posing numerous challenges for programmers building user applications on top of them. For example, if a prompt is specified as a character string, it must be tokenized before passing it to the token-level language model. Thus, the tokenizer and consequent analyses are very sensitive to the specification of the prompt (e.g., if the prompt ends with a space or not). This paper presents algorithms for converting token-level language models to character-level ones. We present both exact and approximate algorithms. In the empirical portion of the paper, we benchmark the practical runtime and approximation quality. We find that -- even with a small computation budget -- our method is able to accurately approximate the character-level distribution (less than 0.00021 excess bits / character) at reasonably fast speeds (46.3 characters / second) on the Llama 3.1 8B language model.
On the Proper Treatment of Tokenization in Psycholinguistics
Oct 03, 2024
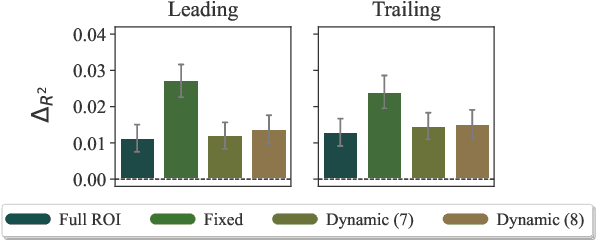

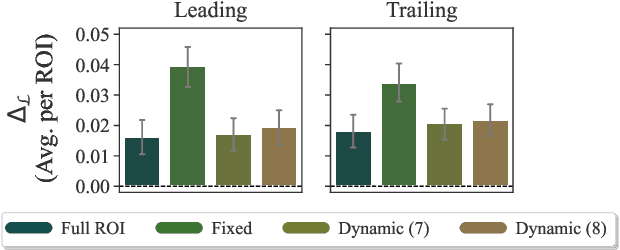
Abstract:Language models are widely used in computational psycholinguistics to test theories that relate the negative log probability (the surprisal) of a region of interest (a substring of characters) under a language model to its cognitive cost experienced by readers, as operationalized, for example, by gaze duration on the region. However, the application of modern language models to psycholinguistic studies is complicated by the practice of using tokenization as an intermediate step in training a model. Doing so results in a language model over token strings rather than one over character strings. Vexingly, regions of interest are generally misaligned with these token strings. The paper argues that token-level language models should be (approximately) marginalized into character-level language models before they are used in psycholinguistic studies to compute the surprisal of a region of interest; then, the marginalized character-level language model can be used to compute the surprisal of an arbitrary character substring, which we term a focal area, that the experimenter may wish to use as a predictor. Our proposal of marginalizing a token-level model into a character-level one solves this misalignment issue independently of the tokenization scheme. Empirically, we discover various focal areas whose surprisal is a better psychometric predictor than the surprisal of the region of interest itself.
The Foundations of Tokenization: Statistical and Computational Concerns
Jul 16, 2024Abstract:Tokenization - the practice of converting strings of characters over an alphabet into sequences of tokens over a vocabulary - is a critical yet under-theorized step in the NLP pipeline. Notably, it remains the only major step not fully integrated into widely used end-to-end neural models. This paper aims to address this theoretical gap by laying the foundations of tokenization from a formal perspective. By articulating and extending basic properties about the category of stochastic maps, we propose a unified framework for representing and analyzing tokenizer models. This framework allows us to establish general conditions for the use of tokenizers. In particular, we formally establish the necessary and sufficient conditions for a tokenizer model to preserve the consistency of statistical estimators. Additionally, we discuss statistical and computational concerns crucial for the design and implementation of tokenizer models. The framework and results advanced in this paper represent a step toward a robust theoretical foundation for neural language modeling.
Tokenization and the Noiseless Channel
Jun 29, 2023
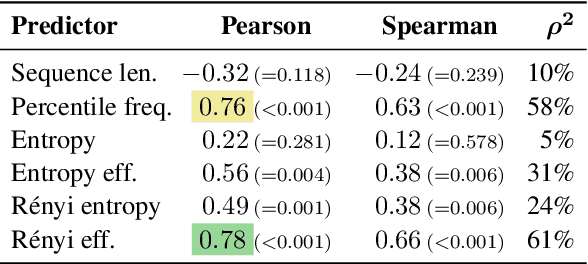
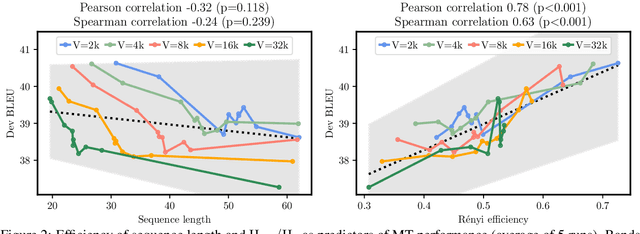
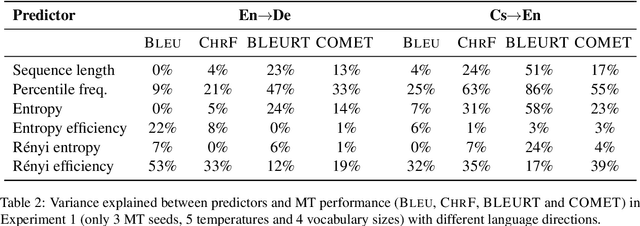
Abstract:Subword tokenization is a key part of many NLP pipelines. However, little is known about why some tokenizer and hyperparameter combinations lead to better downstream model performance than others. We propose that good tokenizers lead to \emph{efficient} channel usage, where the channel is the means by which some input is conveyed to the model and efficiency can be quantified in information-theoretic terms as the ratio of the Shannon entropy to the maximum possible entropy of the token distribution. Yet, an optimal encoding according to Shannon entropy assigns extremely long codes to low-frequency tokens and very short codes to high-frequency tokens. Defining efficiency in terms of R\'enyi entropy, on the other hand, penalizes distributions with either very high or very low-frequency tokens. In machine translation, we find that across multiple tokenizers, the R\'enyi entropy with $\alpha = 2.5$ has a very strong correlation with \textsc{Bleu}: $0.78$ in comparison to just $-0.32$ for compressed length.
A Formal Perspective on Byte-Pair Encoding
Jun 29, 2023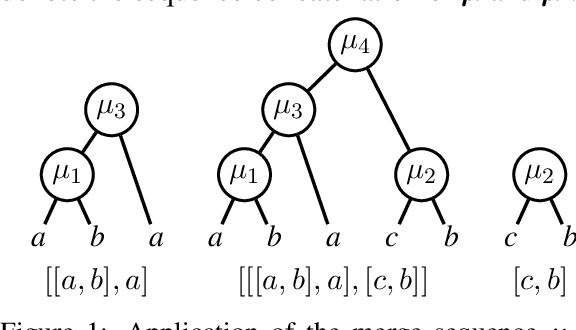

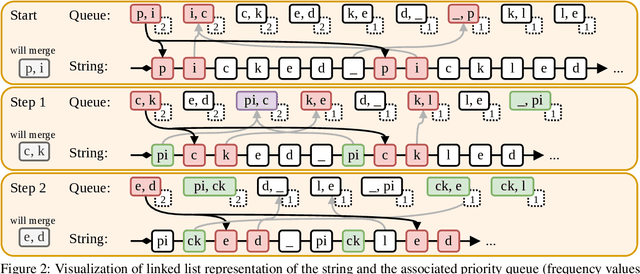
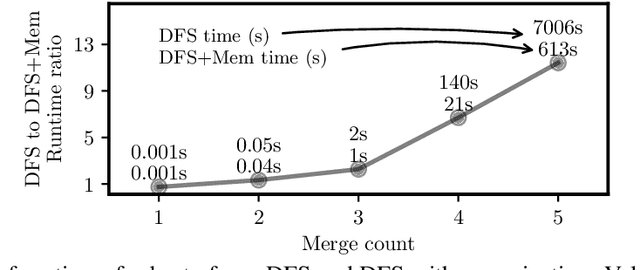
Abstract:Byte-Pair Encoding (BPE) is a popular algorithm used for tokenizing data in NLP, despite being devised initially as a compression method. BPE appears to be a greedy algorithm at face value, but the underlying optimization problem that BPE seeks to solve has not yet been laid down. We formalize BPE as a combinatorial optimization problem. Via submodular functions, we prove that the iterative greedy version is a $\frac{1}{{\sigma(\boldsymbol{\mu}^\star)}}(1-e^{-{\sigma(\boldsymbol{\mu}^\star)}})$-approximation of an optimal merge sequence, where ${\sigma(\boldsymbol{\mu}^\star)}$ is the total backward curvature with respect to the optimal merge sequence $\boldsymbol{\mu}^\star$. Empirically the lower bound of the approximation is $\approx 0.37$. We provide a faster implementation of BPE which improves the runtime complexity from $\mathcal{O}\left(N M\right)$ to $\mathcal{O}\left(N \log M\right)$, where $N$ is the sequence length and $M$ is the merge count. Finally, we optimize the brute-force algorithm for optimal BPE using memoization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge