Tokenization and the Noiseless Channel
Paper and Code
Jun 29, 2023
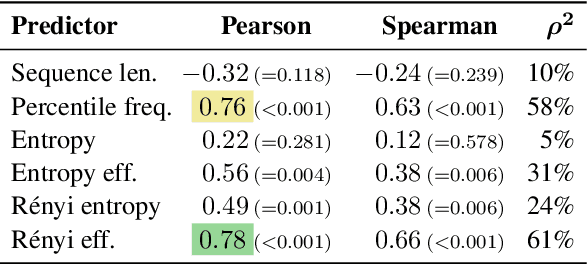
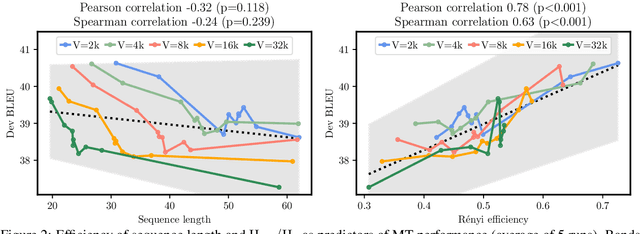
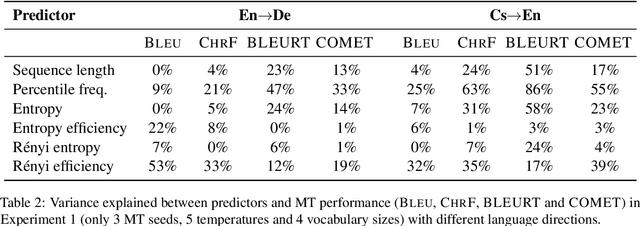
Subword tokenization is a key part of many NLP pipelines. However, little is known about why some tokenizer and hyperparameter combinations lead to better downstream model performance than others. We propose that good tokenizers lead to \emph{efficient} channel usage, where the channel is the means by which some input is conveyed to the model and efficiency can be quantified in information-theoretic terms as the ratio of the Shannon entropy to the maximum possible entropy of the token distribution. Yet, an optimal encoding according to Shannon entropy assigns extremely long codes to low-frequency tokens and very short codes to high-frequency tokens. Defining efficiency in terms of R\'enyi entropy, on the other hand, penalizes distributions with either very high or very low-frequency tokens. In machine translation, we find that across multiple tokenizers, the R\'enyi entropy with $\alpha = 2.5$ has a very strong correlation with \textsc{Bleu}: $0.78$ in comparison to just $-0.32$ for compressed length.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge