Tai-Danae Bradley
Graduate Center, CUNY
The Magnitude of Categories of Texts Enriched by Language Models
Jan 11, 2025

Abstract:The purpose of this article is twofold. Firstly, we use the next-token probabilities given by a language model to explicitly define a $[0,1]$-enrichment of a category of texts in natural language, in the sense of Bradley, Terilla, and Vlassopoulos. We consider explicitly the terminating conditions for text generation and determine when the enrichment itself can be interpreted as a probability over texts. Secondly, we compute the M\"obius function and the magnitude of an associated generalized metric space $\mathcal{M}$ of texts using a combinatorial version of these quantities recently introduced by Vigneaux. The magnitude function $f(t)$ of $\mathcal{M}$ is a sum over texts $x$ (prompts) of the Tsallis $t$-entropies of the next-token probability distributions $p(-|x)$ plus the cardinality of the model's possible outputs. The derivative of $f$ at $t=1$ recovers a sum of Shannon entropies, which justifies seeing magnitude as a partition function. Following Leinster and Schulman, we also express the magnitude function of $\mathcal M$ as an Euler characteristic of magnitude homology and provide an explicit description of the zeroeth and first magnitude homology groups.
Towards structure-preserving quantum encodings
Dec 23, 2024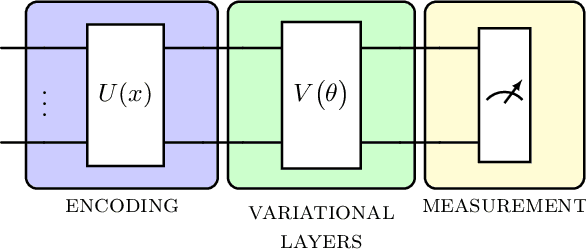
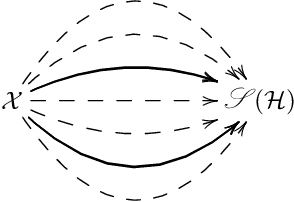
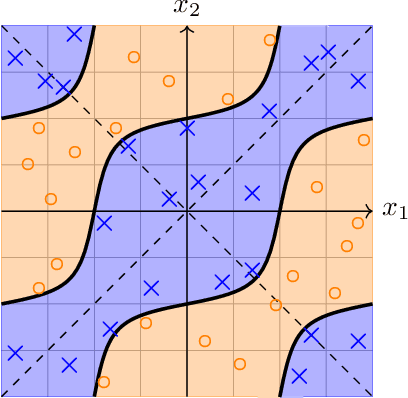
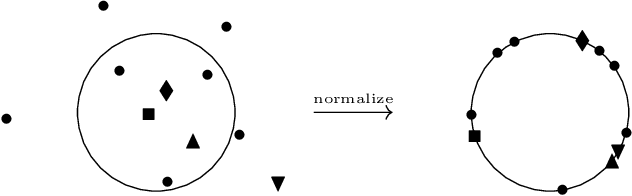
Abstract:Harnessing the potential computational advantage of quantum computers for machine learning tasks relies on the uploading of classical data onto quantum computers through what are commonly referred to as quantum encodings. The choice of such encodings may vary substantially from one task to another, and there exist only a few cases where structure has provided insight into their design and implementation, such as symmetry in geometric quantum learning. Here, we propose the perspective that category theory offers a natural mathematical framework for analyzing encodings that respect structure inherent in datasets and learning tasks. We illustrate this with pedagogical examples, which include geometric quantum machine learning, quantum metric learning, topological data analysis, and more. Moreover, our perspective provides a language in which to ask meaningful and mathematically precise questions for the design of quantum encodings and circuits for quantum machine learning tasks.
Probabilistic Graphical Models and Tensor Networks: A Hybrid Framework
Jun 29, 2021



Abstract:We investigate a correspondence between two formalisms for discrete probabilistic modeling: probabilistic graphical models (PGMs) and tensor networks (TNs), a powerful modeling framework for simulating complex quantum systems. The graphical calculus of PGMs and TNs exhibits many similarities, with discrete undirected graphical models (UGMs) being a special case of TNs. However, more general probabilistic TN models such as Born machines (BMs) employ complex-valued hidden states to produce novel forms of correlation among the probabilities. While representing a new modeling resource for capturing structure in discrete probability distributions, this behavior also renders the direct application of standard PGM tools impossible. We aim to bridge this gap by introducing a hybrid PGM-TN formalism that integrates quantum-like correlations into PGM models in a principled manner, using the physically-motivated concept of decoherence. We first prove that applying decoherence to the entirety of a BM model converts it into a discrete UGM, and conversely, that any subgraph of a discrete UGM can be represented as a decohered BM. This method allows a broad family of probabilistic TN models to be encoded as partially decohered BMs, a fact we leverage to combine the representational strengths of both model families. We experimentally verify the performance of such hybrid models in a sequential modeling task, and identify promising uses of our method within the context of existing applications of graphical models.
An enriched category theory of language: from syntax to semantics
Jun 15, 2021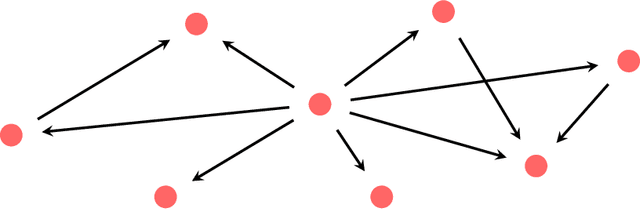
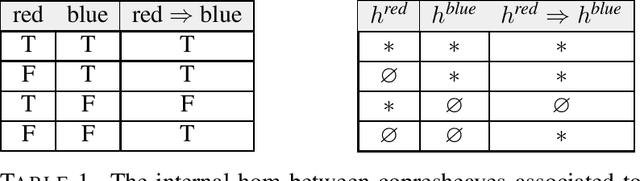
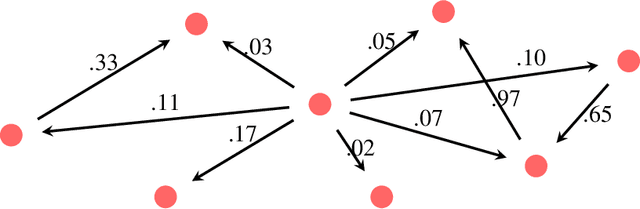
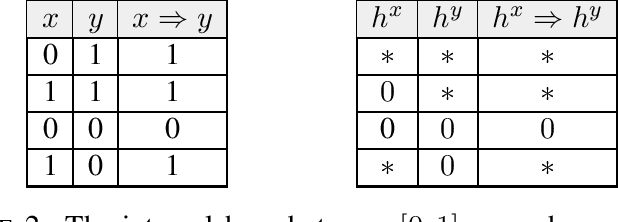
Abstract:Given a piece of text, the ability to generate a coherent extension of it implies some sophistication, including a knowledge of grammar and semantics. In this paper, we propose a mathematical framework for passing from probability distributions on extensions of given texts to an enriched category containing semantic information. Roughly speaking, we model probability distributions on texts as a category enriched over the unit interval. Objects of this category are expressions in language and hom objects are conditional probabilities that one expression is an extension of another. This category is syntactical: it describes what goes with what. We then pass to the enriched category of unit interval-valued copresheaves on this syntactical category to find semantic information.
Language Modeling with Reduced Densities
Jul 08, 2020
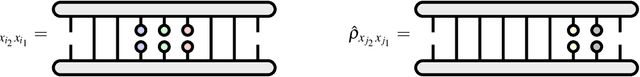
Abstract:We present a framework for modeling words, phrases, and longer expressions in a natural language using reduced density operators. We show these operators capture something of the meaning of these expressions and, under the Loewner order on positive semidefinite operators, preserve both a simple form of entailment and the relevant statistics therein. Pulling back the curtain, the assignment is shown to be a functor between categories enriched over probabilities.
At the Interface of Algebra and Statistics
Apr 12, 2020



Abstract:This thesis takes inspiration from quantum physics to investigate mathematical structure that lies at the interface of algebra and statistics. The starting point is a passage from classical probability theory to quantum probability theory. The quantum version of a probability distribution is a density operator, the quantum version of marginalizing is an operation called the partial trace, and the quantum version of a marginal probability distribution is a reduced density operator. Every joint probability distribution on a finite set can be modeled as a rank one density operator. By applying the partial trace, we obtain reduced density operators whose diagonals recover classical marginal probabilities. In general, these reduced densities will have rank higher than one, and their eigenvalues and eigenvectors will contain extra information that encodes subsystem interactions governed by statistics. We decode this information, and show it is akin to conditional probability, and then investigate the extent to which the eigenvectors capture "concepts" inherent in the original joint distribution. The theory is then illustrated with an experiment that exploits these ideas. Turning to a more theoretical application, we also discuss a preliminary framework for modeling entailment and concept hierarchy in natural language, namely, by representing expressions in the language as densities. Finally, initial inspiration for this thesis comes from formal concept analysis, which finds many striking parallels with the linear algebra. The parallels are not coincidental, and a common blueprint is found in category theory. We close with an exposition on free (co)completions and how the free-forgetful adjunctions in which they arise strongly suggest that in certain categorical contexts, the "fixed points" of a morphism with its adjoint encode interesting information.
Modeling Sequences with Quantum States: A Look Under the Hood
Oct 16, 2019



Abstract:Classical probability distributions on sets of sequences can be modeled using quantum states. Here, we do so with a quantum state that is pure and entangled. Because it is entangled, the reduced densities that describe subsystems also carry information about the complementary subsystem. This is in contrast to the classical marginal distributions on a subsystem in which information about the complementary system has been integrated out and lost. A training algorithm based on the density matrix renormalization group (DMRG) procedure uses the extra information contained in the reduced densities and organizes it into a tensor network model. An understanding of the extra information contained in the reduced densities allow us to examine the mechanics of this DMRG algorithm and study the generalization error of the resulting model. As an illustration, we work with the even-parity dataset and produce an estimate for the generalization error as a function of the fraction of the dataset used in training.
Translating and Evolving: Towards a Model of Language Change in DisCoCat
Nov 08, 2018Abstract:The categorical compositional distributional (DisCoCat) model of meaning developed by Coecke et al. (2010) has been successful in modeling various aspects of meaning. However, it fails to model the fact that language can change. We give an approach to DisCoCat that allows us to represent language models and translations between them, enabling us to describe translations from one language to another, or changes within the same language. We unify the product space representation given in (Coecke et al., 2010) and the functorial description in (Kartsaklis et al., 2013), in a way that allows us to view a language as a catalogue of meanings. We formalize the notion of a lexicon in DisCoCat, and define a dictionary of meanings between two lexicons. All this is done within the framework of monoidal categories. We give examples of how to apply our methods, and give a concrete suggestion for compositional translation in corpora.
* In Proceedings CAPNS 2018, arXiv:1811.02701
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge