Towards structure-preserving quantum encodings

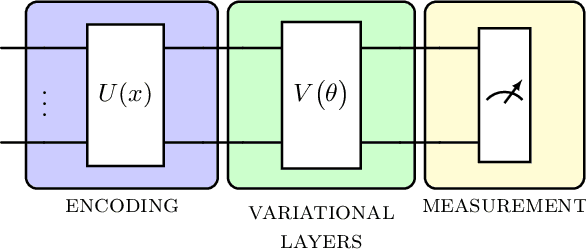
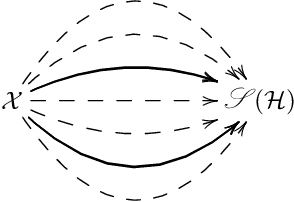
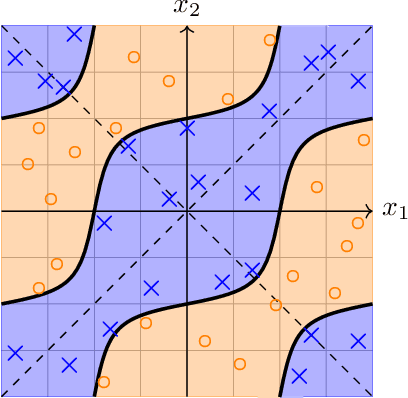
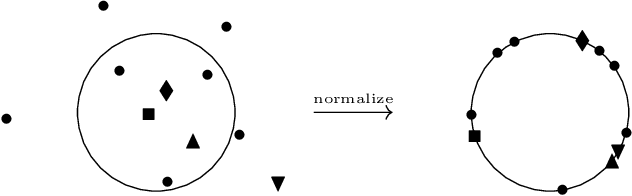
Harnessing the potential computational advantage of quantum computers for machine learning tasks relies on the uploading of classical data onto quantum computers through what are commonly referred to as quantum encodings. The choice of such encodings may vary substantially from one task to another, and there exist only a few cases where structure has provided insight into their design and implementation, such as symmetry in geometric quantum learning. Here, we propose the perspective that category theory offers a natural mathematical framework for analyzing encodings that respect structure inherent in datasets and learning tasks. We illustrate this with pedagogical examples, which include geometric quantum machine learning, quantum metric learning, topological data analysis, and more. Moreover, our perspective provides a language in which to ask meaningful and mathematically precise questions for the design of quantum encodings and circuits for quantum machine learning tasks.

Hybrid Quantum Graph Neural Network for Molecular Property Prediction

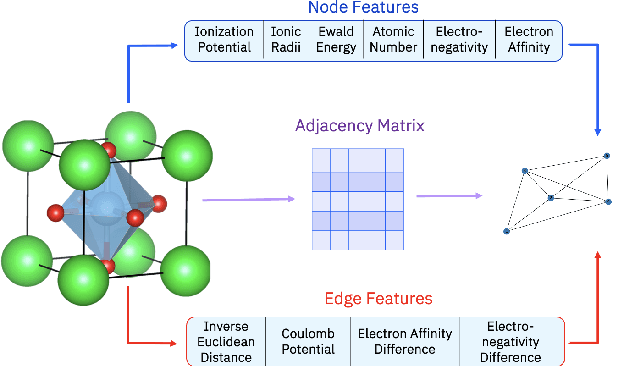
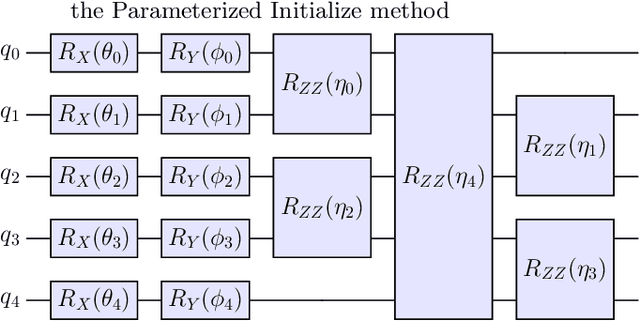
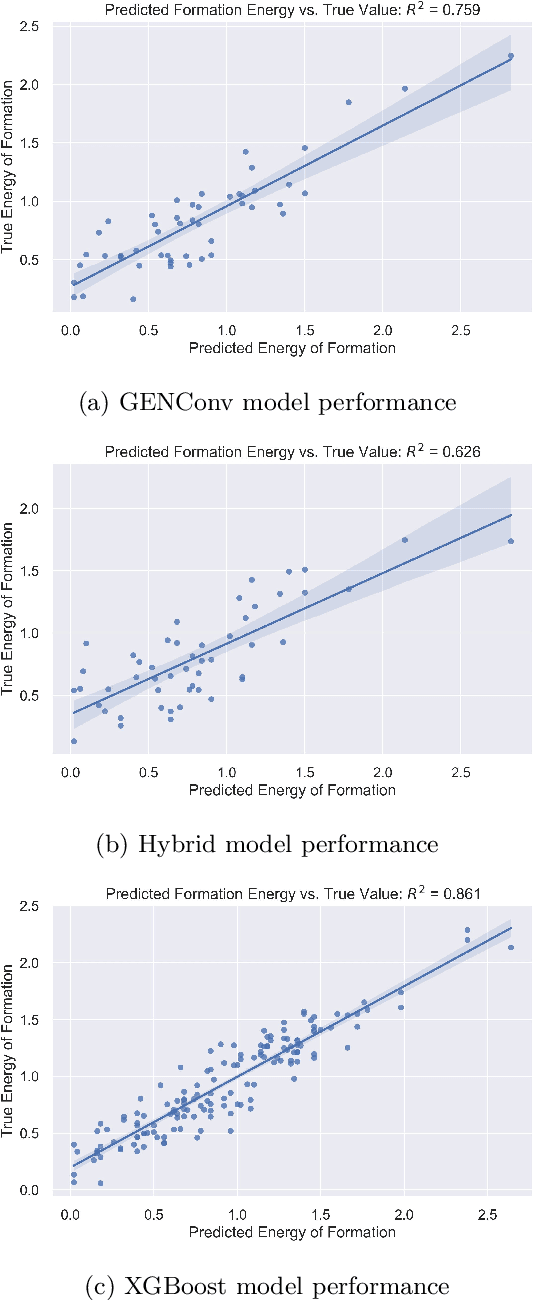
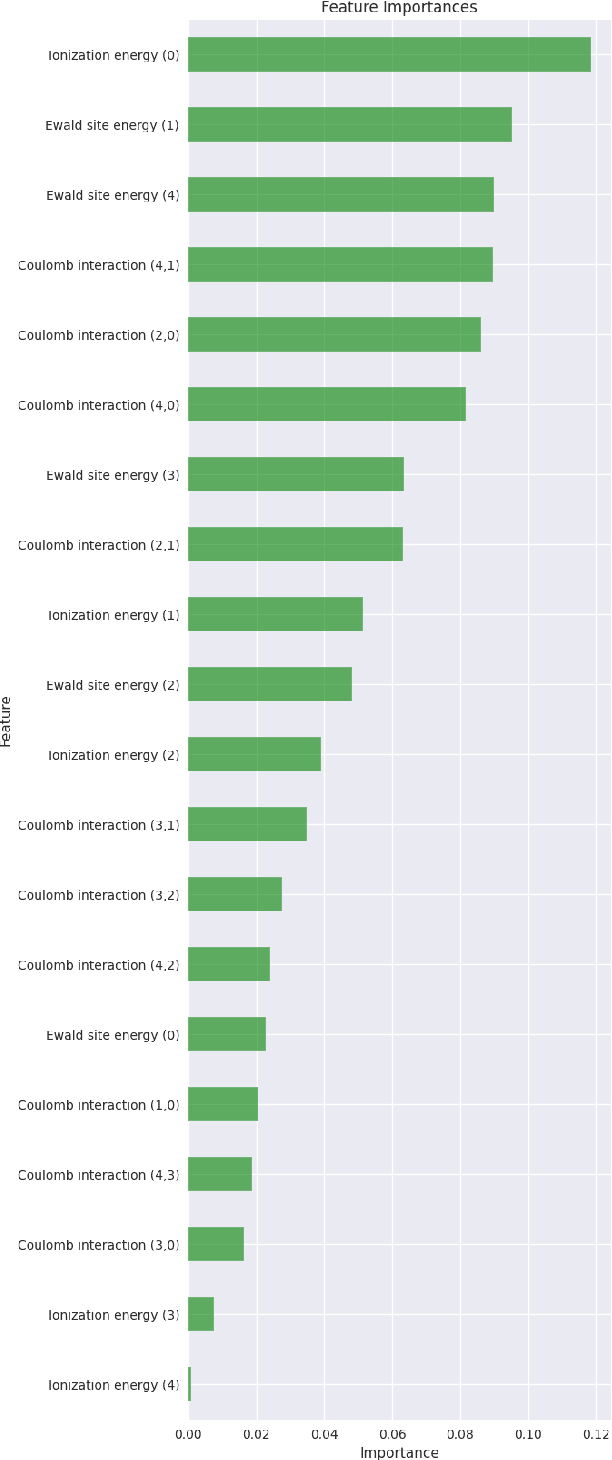
To accelerate the process of materials design, materials science has increasingly used data driven techniques to extract information from collected data. Specially, machine learning (ML) algorithms, which span the ML discipline, have demonstrated ability to predict various properties of materials with the level of accuracy similar to explicit calculation of quantum mechanical theories, but with significantly reduced run time and computational resources. Within ML, graph neural networks have emerged as an important algorithm within the field of machine learning, since they are capable of predicting accurately a wide range of important physical, chemical and electronic properties due to their higher learning ability based on the graph representation of material and molecular descriptors through the aggregation of information embedded within the graph. In parallel with the development of state of the art classical machine learning applications, the fusion of quantum computing and machine learning have created a new paradigm where classical machine learning model can be augmented with quantum layers which are able to encode high dimensional data more efficiently. Leveraging the structure of existing algorithms, we developed a unique and novel gradient free hybrid quantum classical convoluted graph neural network (HyQCGNN) to predict formation energies of perovskite materials. The performance of our hybrid statistical model is competitive with the results obtained purely from a classical convoluted graph neural network, and other classical machine learning algorithms, such as XGBoost. Consequently, our study suggests a new pathway to explore how quantum feature encoding and parametric quantum circuits can yield drastic improvements of complex ML algorithm like graph neural network.

Conditional Generative Models for Learning Stochastic Processes

A framework to learn a multi-modal distribution is proposed, denoted as the Conditional Quantum Generative Adversarial Network (C-qGAN). The neural network structure is strictly within a quantum circuit and, as a consequence, is shown to represent a more efficient state preparation procedure than current methods. This methodology has the potential to speed-up algorithms, such as Monte Carlo analysis. In particular, after demonstrating the effectiveness of the network in the learning task, the technique is applied to price Asian option derivatives, providing the foundation for further research on other path-dependent options.

Quantum Kernel for Image Classification of Real World Manufacturing Defects

The quantum kernel method results clearly outperformed a classical SVM when analyzing low-resolution images with minimal feature selection on the quantum simulator, with inconsistent results when run on an actual quantum processor. We chose to use an existing quantum kernel method for classification. We applied dynamic decoupling error mitigation using the Mitiq package to the Quantum SVM kernel method, which, to our knowledge, has never been done for quantum kernel methods for image classification. We applied the quantum kernel method to classify real world image data from a manufacturing facility using a superconducting quantum computer. The manufacturing images were used to determine if a product was defective or was produced correctly through the manufacturing process. We also tested the Mitiq dynamical decoupling (DD) methodology to understand effectiveness in decreasing noise-related errors. We also found that the way classical data was encoded onto qubits in quantum states affected our results. All three quantum processing unit (QPU) runs of our angle encoded circuit returned different results, with one run having better than classical results, one run having equivalent to classical results, and a run with worse than classical results. The more complex instantaneous quantum polynomial (IQP) encoding approach showed better precision than classical SVM results when run on a QPU but had a worse recall and F1-score. We found that DD error mitigation did not improve the results of IQP encoded circuits runs and did not have an impact on angle encoded circuits runs on the QPU. In summary, we found that the angle encoded circuit performed the best of the quantum kernel encoding methods on real quantum hardware. In future research projects using quantum kernels to classify images, we recommend exploring other error mitigation techniques than Mitiq DD.