Towards structure-preserving quantum encodings

Harnessing the potential computational advantage of quantum computers for machine learning tasks relies on the uploading of classical data onto quantum computers through what are commonly referred to as quantum encodings. The choice of such encodings may vary substantially from one task to another, and there exist only a few cases where structure has provided insight into their design and implementation, such as symmetry in geometric quantum learning. Here, we propose the perspective that category theory offers a natural mathematical framework for analyzing encodings that respect structure inherent in datasets and learning tasks. We illustrate this with pedagogical examples, which include geometric quantum machine learning, quantum metric learning, topological data analysis, and more. Moreover, our perspective provides a language in which to ask meaningful and mathematically precise questions for the design of quantum encodings and circuits for quantum machine learning tasks.

Hybrid Quantum Graph Neural Network for Molecular Property Prediction

To accelerate the process of materials design, materials science has increasingly used data driven techniques to extract information from collected data. Specially, machine learning (ML) algorithms, which span the ML discipline, have demonstrated ability to predict various properties of materials with the level of accuracy similar to explicit calculation of quantum mechanical theories, but with significantly reduced run time and computational resources. Within ML, graph neural networks have emerged as an important algorithm within the field of machine learning, since they are capable of predicting accurately a wide range of important physical, chemical and electronic properties due to their higher learning ability based on the graph representation of material and molecular descriptors through the aggregation of information embedded within the graph. In parallel with the development of state of the art classical machine learning applications, the fusion of quantum computing and machine learning have created a new paradigm where classical machine learning model can be augmented with quantum layers which are able to encode high dimensional data more efficiently. Leveraging the structure of existing algorithms, we developed a unique and novel gradient free hybrid quantum classical convoluted graph neural network (HyQCGNN) to predict formation energies of perovskite materials. The performance of our hybrid statistical model is competitive with the results obtained purely from a classical convoluted graph neural network, and other classical machine learning algorithms, such as XGBoost. Consequently, our study suggests a new pathway to explore how quantum feature encoding and parametric quantum circuits can yield drastic improvements of complex ML algorithm like graph neural network.

Conditional Generative Models for Learning Stochastic Processes

A framework to learn a multi-modal distribution is proposed, denoted as the Conditional Quantum Generative Adversarial Network (C-qGAN). The neural network structure is strictly within a quantum circuit and, as a consequence, is shown to represent a more efficient state preparation procedure than current methods. This methodology has the potential to speed-up algorithms, such as Monte Carlo analysis. In particular, after demonstrating the effectiveness of the network in the learning task, the technique is applied to price Asian option derivatives, providing the foundation for further research on other path-dependent options.

An Advantage Using Feature Selection with a Quantum Annealer

Feature selection is a technique in statistical prediction modeling that identifies features in a record with a strong statistical connection to the target variable. Excluding features with a weak statistical connection to the target variable in training not only drops the dimension of the data, which decreases the time complexity of the algorithm, it also decreases noise within the data which assists in avoiding overfitting. In all, feature selection assists in training a robust statistical model that performs well and is stable. Given the lack of scalability in classical computation, current techniques only consider the predictive power of the feature and not redundancy between the features themselves. Recent advancements in feature selection that leverages quantum annealing (QA) gives a scalable technique that aims to maximize the predictive power of the features while minimizing redundancy. As a consequence, it is expected that this algorithm would assist in the bias/variance trade-off yielding better features for training a statistical model. This paper tests this intuition against classical methods by utilizing open-source data sets and evaluate the efficacy of each trained statistical model well-known prediction algorithms. The numerical results display an advantage utilizing the features selected from the algorithm that leveraged QA.

$α$QBoost: An Iteratively Weighted Adiabatic Trained Classifier

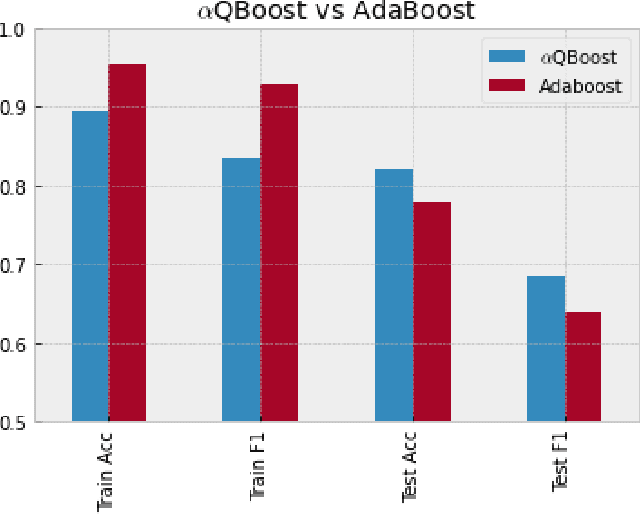
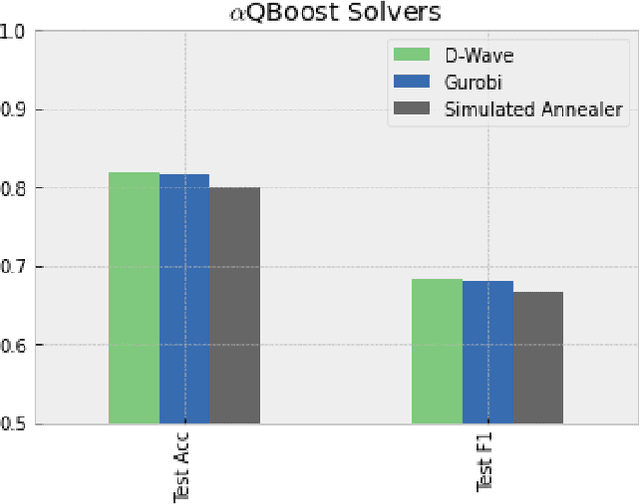
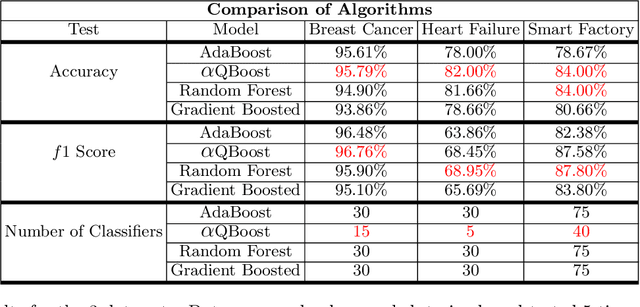
A new implementation of an adiabatically-trained ensemble model is derived that shows significant improvements over classical methods. In particular, empirical results of this new algorithm show that it offers not just higher performance, but also more stability with less classifiers, an attribute that is critically important in areas like explainability and speed-of-inference. In all, the empirical analysis displays that the algorithm can provide an increase in performance on unseen data by strengthening stability of the statistical model through further minimizing and balancing variance and bias, while decreasing the time to convergence over its predecessors.