Directed Metric Structures arising in Large Language Models

Large Language Models are transformer neural networks which are trained to produce a probability distribution on the possible next words to given texts in a corpus, in such a way that the most likely word predicted is the actual word in the training text. In this paper we find what is the mathematical structure defined by such conditional probability distributions of text extensions. Changing the view point from probabilities to -log probabilities we observe that the subtext order is completely encoded in a metric structure defined on the space of texts $\mathcal{L}$, by -log probabilities. We then construct a metric polyhedron $P(\mathcal{L})$ and an isometric embedding (called Yoneda embedding) of $\mathcal{L}$ into $P(\mathcal{L})$ such that texts map to generators of certain special extremal rays. We explain that $P(\mathcal{L})$ is a $(\min,+)$ (tropical) linear span of these extremal ray generators. The generators also satisfy a system of $(\min+)$ linear equations. We then show that $P(\mathcal{L})$ is compatible with adding more text and from this we derive an approximation of a text vector as a Boltzmann weighted linear combination of the vectors for words in that text. We then prove a duality theorem showing that texts extensions and text restrictions give isometric polyhedra (even though they look a priory very different). Moreover we prove that $P(\mathcal{L})$ is the lattice closure of (a version of) the so called, Isbell completion of $\mathcal{L}$ which turns out to be the $(\max,+)$ span of the text extremal ray generators. All constructions have interpretations in category theory but we don't use category theory explicitly. The categorical interpretations are briefly explained in an appendix. In the final appendix we describe how the syntax to semantics problem could fit in a general well known mathematical duality.

An enriched category theory of language: from syntax to semantics

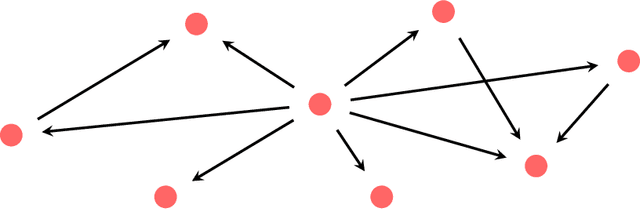
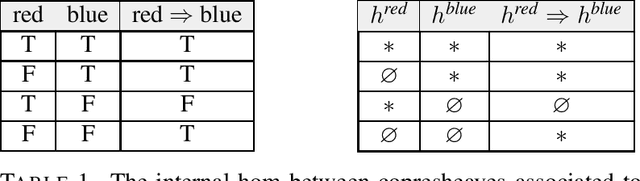
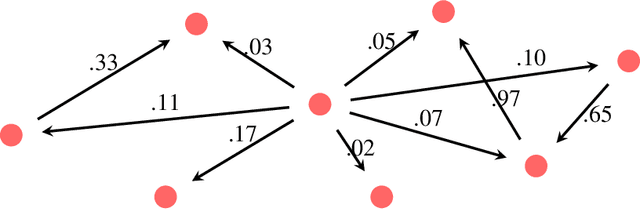
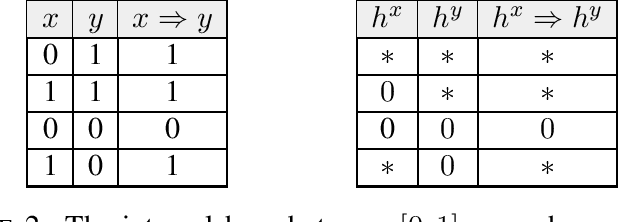
Given a piece of text, the ability to generate a coherent extension of it implies some sophistication, including a knowledge of grammar and semantics. In this paper, we propose a mathematical framework for passing from probability distributions on extensions of given texts to an enriched category containing semantic information. Roughly speaking, we model probability distributions on texts as a category enriched over the unit interval. Objects of this category are expressions in language and hom objects are conditional probabilities that one expression is an extension of another. This category is syntactical: it describes what goes with what. We then pass to the enriched category of unit interval-valued copresheaves on this syntactical category to find semantic information.

Language Modeling with Reduced Densities

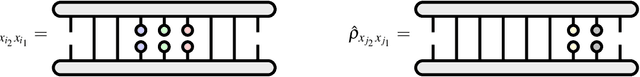
We present a framework for modeling words, phrases, and longer expressions in a natural language using reduced density operators. We show these operators capture something of the meaning of these expressions and, under the Loewner order on positive semidefinite operators, preserve both a simple form of entailment and the relevant statistics therein. Pulling back the curtain, the assignment is shown to be a functor between categories enriched over probabilities.

Language as a matrix product state

We propose a statistical model for natural language that begins by considering language as a monoid, then representing it in complex matrices with a compatible translation invariant probability measure. We interpret the probability measure as arising via the Born rule from a translation invariant matrix product state.

Tensor network language model

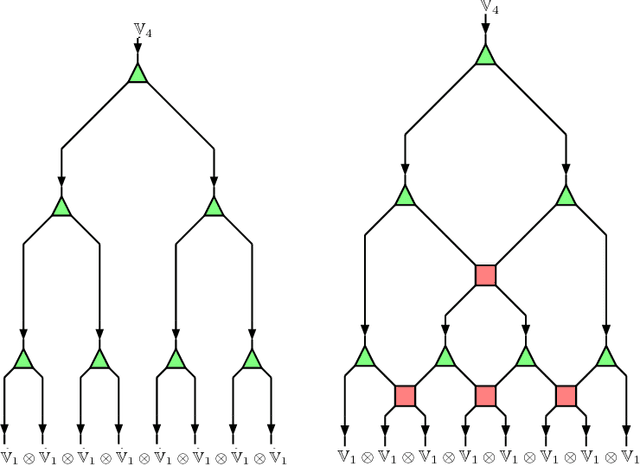
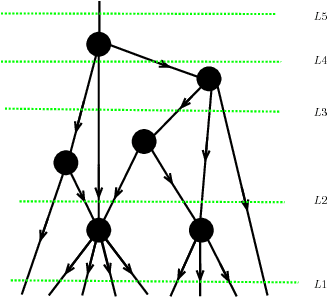
We propose a new statistical model suitable for machine learning of systems with long distance correlations such as natural languages. The model is based on directed acyclic graph decorated by multi-linear tensor maps in the vertices and vector spaces in the edges, called tensor network. Such tensor networks have been previously employed for effective numerical computation of the renormalization group flow on the space of effective quantum field theories and lattice models of statistical mechanics. We provide explicit algebro-geometric analysis of the parameter moduli space for tree graphs, discuss model properties and applications such as statistical translation.