Graph2Tac: Learning Hierarchical Representations of Math Concepts in Theorem proving

Concepts abound in mathematics and its applications. They vary greatly between subject areas, and new ones are introduced in each mathematical paper or application. A formal theory builds a hierarchy of definitions, theorems and proofs that reference each other. When an AI agent is proving a new theorem, most of the mathematical concepts and lemmas relevant to that theorem may have never been seen during training. This is especially true in the Coq proof assistant, which has a diverse library of Coq projects, each with its own definitions, lemmas, and even custom tactic procedures used to prove those lemmas. It is essential for agents to incorporate such new information into their knowledge base on the fly. We work towards this goal by utilizing a new, large-scale, graph-based dataset for machine learning in Coq. We leverage a faithful graph-representation of Coq terms that induces a directed graph of dependencies between definitions to create a novel graph neural network, Graph2Tac (G2T), that takes into account not only the current goal, but also the entire hierarchy of definitions that led to the current goal. G2T is an online model that is deeply integrated into the users' workflow and can adapt in real time to new Coq projects and their definitions. It complements well with other online models that learn in real time from new proof scripts. Our novel definition embedding task, which is trained to compute representations of mathematical concepts not seen during training, boosts the performance of the neural network to rival state-of-the-art k-nearest neighbor predictors.

Formalization of a Stochastic Approximation Theorem

Stochastic approximation algorithms are iterative procedures which are used to approximate a target value in an environment where the target is unknown and direct observations are corrupted by noise. These algorithms are useful, for instance, for root-finding and function minimization when the target function or model is not directly known. Originally introduced in a 1951 paper by Robbins and Monro, the field of Stochastic approximation has grown enormously and has come to influence application domains from adaptive signal processing to artificial intelligence. As an example, the Stochastic Gradient Descent algorithm which is ubiquitous in various subdomains of Machine Learning is based on stochastic approximation theory. In this paper, we give a formal proof (in the Coq proof assistant) of a general convergence theorem due to Aryeh Dvoretzky, which implies the convergence of important classical methods such as the Robbins-Monro and the Kiefer-Wolfowitz algorithms. In the process, we build a comprehensive Coq library of measure-theoretic probability theory and stochastic processes.

CertRL: Formalizing Convergence Proofs for Value and Policy Iteration in Coq

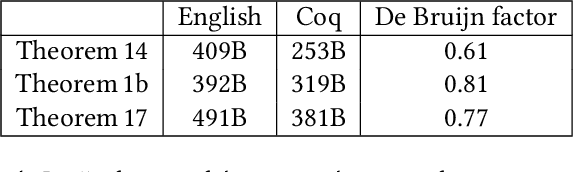
Reinforcement learning algorithms solve sequential decision-making problems in probabilistic environments by optimizing for long-term reward. The desire to use reinforcement learning in safety-critical settings inspires a recent line of work on formally constrained reinforcement learning; however, these methods place the implementation of the learning algorithm in their Trusted Computing Base. The crucial correctness property of these implementations is a guarantee that the learning algorithm converges to an optimal policy. This paper begins the work of closing this gap by developing a Coq formalization of two canonical reinforcement learning algorithms: value and policy iteration for finite state Markov decision processes. The central results are a formalization of Bellman's optimality principle and its proof, which uses a contraction property of Bellman optimality operator to establish that a sequence converges in the infinite horizon limit. The CertRL development exemplifies how the Giry monad and mechanized metric coinduction streamline optimality proofs for reinforcement learning algorithms. The CertRL library provides a general framework for proving properties about Markov decision processes and reinforcement learning algorithms, paving the way for further work on formalization of reinforcement learning algorithms.

Language as a matrix product state

We propose a statistical model for natural language that begins by considering language as a monoid, then representing it in complex matrices with a compatible translation invariant probability measure. We interpret the probability measure as arising via the Born rule from a translation invariant matrix product state.

Tensor network language model

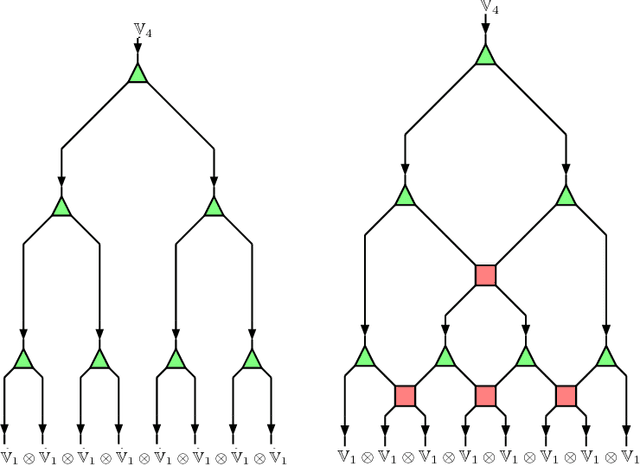
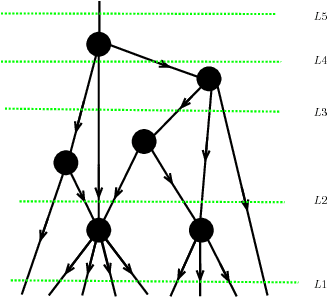
We propose a new statistical model suitable for machine learning of systems with long distance correlations such as natural languages. The model is based on directed acyclic graph decorated by multi-linear tensor maps in the vertices and vector spaces in the edges, called tensor network. Such tensor networks have been previously employed for effective numerical computation of the renormalization group flow on the space of effective quantum field theories and lattice models of statistical mechanics. We provide explicit algebro-geometric analysis of the parameter moduli space for tree graphs, discuss model properties and applications such as statistical translation.