Generative Modeling via Hierarchical Tensor Sketching

We propose a hierarchical tensor-network approach for approximating high-dimensional probability density via empirical distribution. This leverages randomized singular value decomposition (SVD) techniques and involves solving linear equations for tensor cores in this tensor network. The complexity of the resulting algorithm scales linearly in the dimension of the high-dimensional density. An analysis of estimation error demonstrates the effectiveness of this method through several numerical experiments.

Generalization and Overfitting in Matrix Product State Machine Learning Architectures

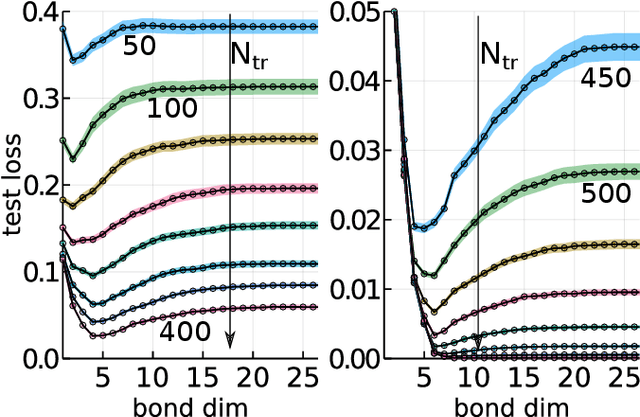
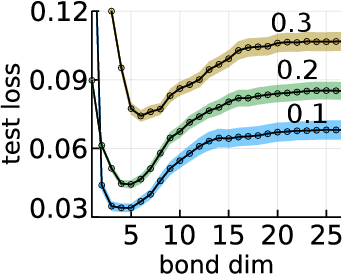
While overfitting and, more generally, double descent are ubiquitous in machine learning, increasing the number of parameters of the most widely used tensor network, the matrix product state (MPS), has generally lead to monotonic improvement of test performance in previous studies. To better understand the generalization properties of architectures parameterized by MPS, we construct artificial data which can be exactly modeled by an MPS and train the models with different number of parameters. We observe model overfitting for one-dimensional data, but also find that for more complex data overfitting is less significant, while with MNIST image data we do not find any signatures of overfitting. We speculate that generalization properties of MPS depend on the properties of data: with one-dimensional data (for which the MPS ansatz is the most suitable) MPS is prone to overfitting, while with more complex data which cannot be fit by MPS exactly, overfitting may be much less significant.

Modeling Sequences with Quantum States: A Look Under the Hood

Classical probability distributions on sets of sequences can be modeled using quantum states. Here, we do so with a quantum state that is pure and entangled. Because it is entangled, the reduced densities that describe subsystems also carry information about the complementary subsystem. This is in contrast to the classical marginal distributions on a subsystem in which information about the complementary system has been integrated out and lost. A training algorithm based on the density matrix renormalization group (DMRG) procedure uses the extra information contained in the reduced densities and organizes it into a tensor network model. An understanding of the extra information contained in the reduced densities allow us to examine the mechanics of this DMRG algorithm and study the generalization error of the resulting model. As an illustration, we work with the even-parity dataset and produce an estimate for the generalization error as a function of the fraction of the dataset used in training.

Towards Quantum Machine Learning with Tensor Networks

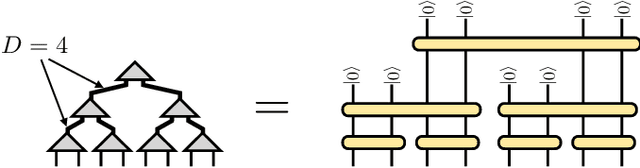
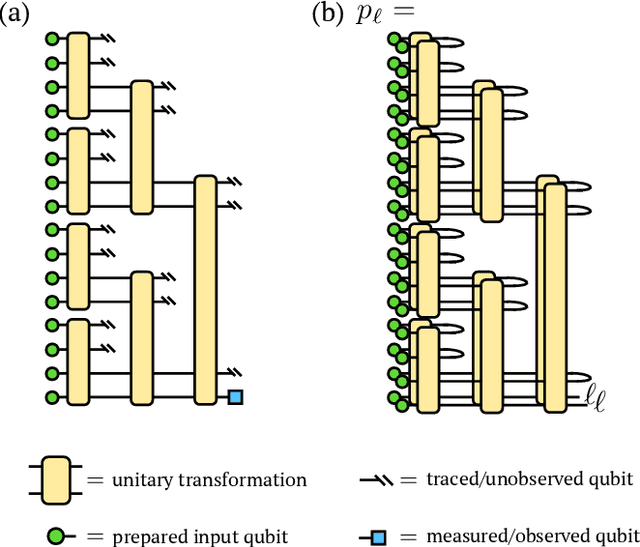
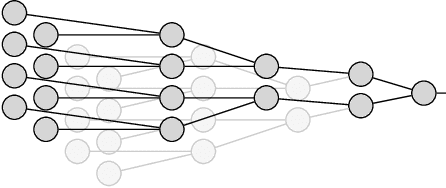
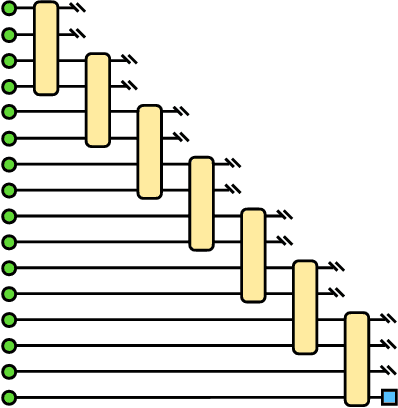
Machine learning is a promising application of quantum computing, but challenges remain as near-term devices will have a limited number of physical qubits and high error rates. Motivated by the usefulness of tensor networks for machine learning in the classical context, we propose quantum computing approaches to both discriminative and generative learning, with circuits based on tree and matrix product state tensor networks that could have benefits for near-term devices. The result is a unified framework where classical and quantum computing can benefit from the same theoretical and algorithmic developments, and the same model can be trained classically then transferred to the quantum setting for additional optimization. Tensor network circuits can also provide qubit-efficient schemes where, depending on the architecture, the number of physical qubits required scales only logarithmically with, or independently of the input or output data sizes. We demonstrate our proposals with numerical experiments, training a discriminative model to perform handwriting recognition using a optimization procedure that could be carried out on quantum hardware, and testing the noise resilience of the trained model.

Supervised Learning with Quantum-Inspired Tensor Networks

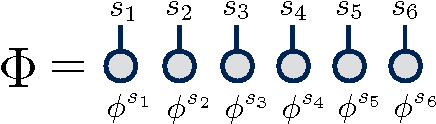
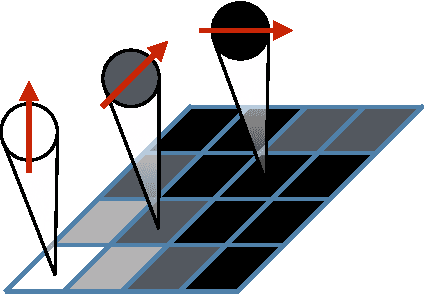
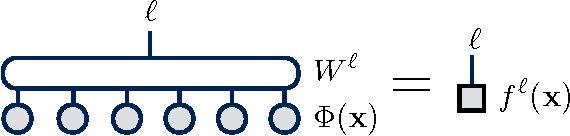
Tensor networks are efficient representations of high-dimensional tensors which have been very successful for physics and mathematics applications. We demonstrate how algorithms for optimizing such networks can be adapted to supervised learning tasks by using matrix product states (tensor trains) to parameterize models for classifying images. For the MNIST data set we obtain less than 1% test set classification error. We discuss how the tensor network form imparts additional structure to the learned model and suggest a possible generative interpretation.