Optimization-Free Diffusion Model -- A Perturbation Theory Approach

Diffusion models have emerged as a powerful framework in generative modeling, typically relying on optimizing neural networks to estimate the score function via forward SDE simulations. In this work, we propose an alternative method that is both optimization-free and forward SDE-free. By expanding the score function in a sparse set of eigenbasis of the backward Kolmogorov operator associated with the diffusion process, we reformulate score estimation as the solution to a linear system, avoiding iterative optimization and time-dependent sample generation. We analyze the approximation error using perturbation theory and demonstrate the effectiveness of our method on high-dimensional Boltzmann distributions and real-world datasets.

Nonparametric Estimation via Variance-Reduced Sketching

Nonparametric models are of great interest in various scientific and engineering disciplines. Classical kernel methods, while numerically robust and statistically sound in low-dimensional settings, become inadequate in higher-dimensional settings due to the curse of dimensionality. In this paper, we introduce a new framework called Variance-Reduced Sketching (VRS), specifically designed to estimate density functions and nonparametric regression functions in higher dimensions with a reduced curse of dimensionality. Our framework conceptualizes multivariable functions as infinite-size matrices, and facilitates a new sketching technique motivated by numerical linear algebra literature to reduce the variance in estimation problems. We demonstrate the robust numerical performance of VRS through a series of simulated experiments and real-world data applications. Notably, VRS shows remarkable improvement over existing neural network estimators and classical kernel methods in numerous density estimation and nonparametric regression models. Additionally, we offer theoretical justifications for VRS to support its ability to deliver nonparametric estimation with a reduced curse of dimensionality.

Matching via Distance Profiles

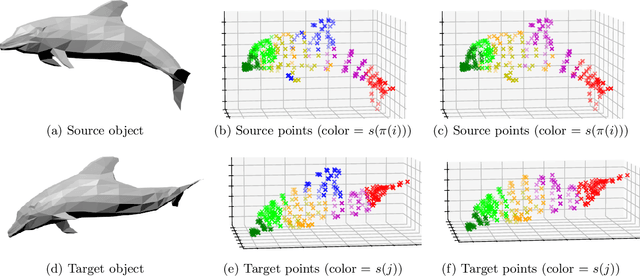
In this paper, we introduce and study matching methods based on distance profiles. For the matching of point clouds, the proposed method is easily implementable by solving a linear program, circumventing the computational obstacles of quadratic matching. Also, we propose and analyze a flexible way to execute location-to-location matching using distance profiles. Moreover, we provide a statistical estimation error analysis in the context of location-to-location matching using empirical process theory. Furthermore, we apply our method to a certain model and show its noise stability by characterizing conditions on the noise level for the matching to be successful. Lastly, we demonstrate the performance of the proposed method and compare it with some existing methods using synthetic and real data.

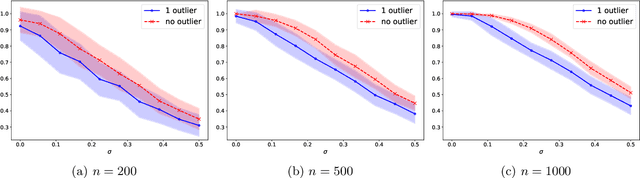
Combining Particle and Tensor-network Methods for Partial Differential Equations via Sketching

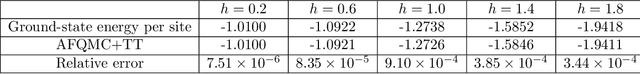
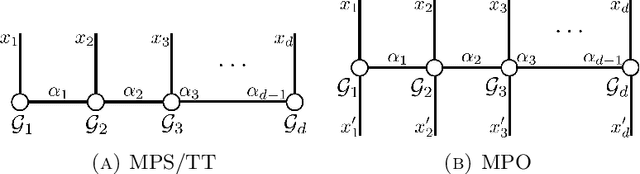
In this paper, we propose a general framework for solving high-dimensional partial differential equations with tensor networks. Our approach offers a comprehensive solution methodology, wherein we employ a combination of particle simulations to update the solution and re-estimations of the new solution as a tensor-network using a recently proposed tensor train sketching technique. Our method can also be interpreted as an alternative approach for performing particle number control by assuming the particles originate from an underlying tensor network. We demonstrate the versatility and flexibility of our approach by applying it to two specific scenarios: simulating the Fokker-Planck equation through Langevin dynamics and quantum imaginary time evolution via auxiliary-field quantum Monte Carlo.

Tensorizing flows: a tool for variational inference

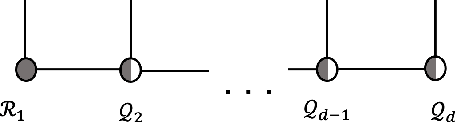
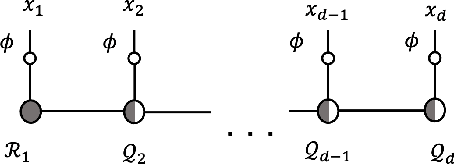
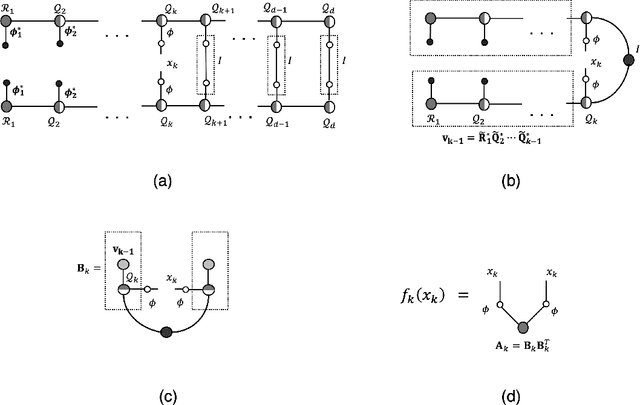
Fueled by the expressive power of deep neural networks, normalizing flows have achieved spectacular success in generative modeling, or learning to draw new samples from a distribution given a finite dataset of training samples. Normalizing flows have also been applied successfully to variational inference, wherein one attempts to learn a sampler based on an expression for the log-likelihood or energy function of the distribution, rather than on data. In variational inference, the unimodality of the reference Gaussian distribution used within the normalizing flow can cause difficulties in learning multimodal distributions. We introduce an extension of normalizing flows in which the Gaussian reference is replaced with a reference distribution that is constructed via a tensor network, specifically a matrix product state or tensor train. We show that by combining flows with tensor networks on difficult variational inference tasks, we can improve on the results obtained by using either tool without the other.

Deep Neural-network Prior for Orbit Recovery from Method of Moments

Orbit recovery problems are a class of problems that often arise in practice and in various forms. In these problems, we aim to estimate an unknown function after being distorted by a group action and observed via a known operator. Typically, the observations are contaminated with a non-trivial level of noise. Two particular orbit recovery problems of interest in this paper are multireference alignment and single-particle cryo-EM modeling. In order to suppress the noise, we suggest using the method of moments approach for both problems while introducing deep neural network priors. In particular, our neural networks should output the signals and the distribution of group elements, with moments being the input. In the multireference alignment case, we demonstrate the advantage of using the NN to accelerate the convergence for the reconstruction of signals from the moments. Finally, we use our method to reconstruct simulated and biological volumes in the cryo-EM setting.

Generative Modeling via Hierarchical Tensor Sketching

We propose a hierarchical tensor-network approach for approximating high-dimensional probability density via empirical distribution. This leverages randomized singular value decomposition (SVD) techniques and involves solving linear equations for tensor cores in this tensor network. The complexity of the resulting algorithm scales linearly in the dimension of the high-dimensional density. An analysis of estimation error demonstrates the effectiveness of this method through several numerical experiments.

High-dimensional density estimation with tensorizing flow

We propose the tensorizing flow method for estimating high-dimensional probability density functions from the observed data. The method is based on tensor-train and flow-based generative modeling. Our method first efficiently constructs an approximate density in the tensor-train form via solving the tensor cores from a linear system based on the kernel density estimators of low-dimensional marginals. We then train a continuous-time flow model from this tensor-train density to the observed empirical distribution by performing a maximum likelihood estimation. The proposed method combines the optimization-less feature of the tensor-train with the flexibility of the flow-based generative models. Numerical results are included to demonstrate the performance of the proposed method.

Generative Modeling via Tree Tensor Network States

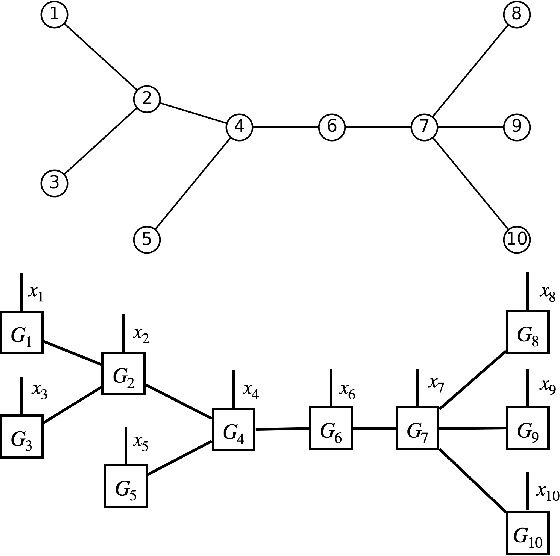
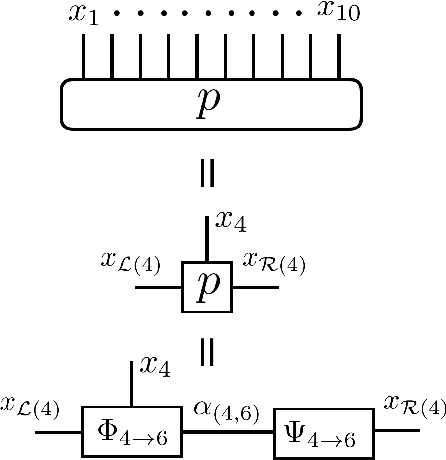
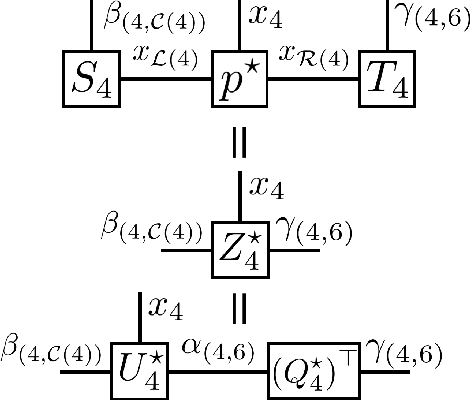
In this paper, we present a density estimation framework based on tree tensor-network states. The proposed method consists of determining the tree topology with Chow-Liu algorithm, and obtaining a linear system of equations that defines the tensor-network components via sketching techniques. Novel choices of sketch functions are developed in order to consider graphical models that contain loops. Sample complexity guarantees are provided and further corroborated by numerical experiments.

Reinforced Inverse Scattering

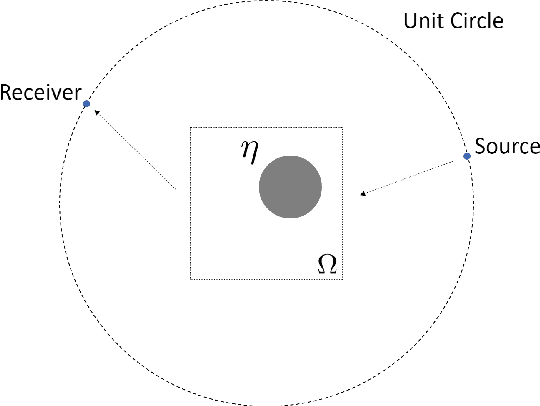
Inverse wave scattering aims at determining the properties of an object using data on how the object scatters incoming waves. In order to collect information, sensors are put in different locations to send and receive waves from each other. The choice of sensor positions and incident wave frequencies determines the reconstruction quality of scatterer properties. This paper introduces reinforcement learning to develop precision imaging that decides sensor positions and wave frequencies adaptive to different scatterers in an intelligent way, thus obtaining a significant improvement in reconstruction quality with limited imaging resources. Extensive numerical results will be provided to demonstrate the superiority of the proposed method over existing methods.