Conformal prediction for multi-dimensional time series by ellipsoidal sets

Conformal prediction (CP) has been a popular method for uncertainty quantification because it is distribution-free, model-agnostic, and theoretically sound. For forecasting problems in supervised learning, most CP methods focus on building prediction intervals for univariate responses. In this work, we develop a sequential CP method called $\texttt{MultiDimSPCI}$ that builds prediction regions for a multivariate response, especially in the context of multivariate time series, which are not exchangeable. Theoretically, we estimate finite-sample high-probability bounds on the conditional coverage gap. Empirically, we demonstrate that $\texttt{MultiDimSPCI}$ maintains valid coverage on a wide range of multivariate time series while producing smaller prediction regions than CP and non-CP baselines.

Mobile Internet Quality Estimation using Self-Tuning Kernel Regression

Modeling and estimation for spatial data are ubiquitous in real life, frequently appearing in weather forecasting, pollution detection, and agriculture. Spatial data analysis often involves processing datasets of enormous scale. In this work, we focus on large-scale internet-quality open datasets from Ookla. We look into estimating mobile (cellular) internet quality at the scale of a state in the United States. In particular, we aim to conduct estimation based on highly {\it imbalanced} data: Most of the samples are concentrated in limited areas, while very few are available in the rest, posing significant challenges to modeling efforts. We propose a new adaptive kernel regression approach that employs self-tuning kernels to alleviate the adverse effects of data imbalance in this problem. Through comparative experimentation on two distinct mobile network measurement datasets, we demonstrate that the proposed self-tuning kernel regression method produces more accurate predictions, with the potential to be applied in other applications.

Reinforced Inverse Scattering

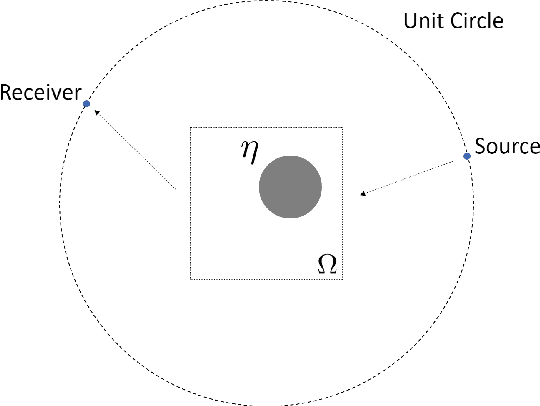
Inverse wave scattering aims at determining the properties of an object using data on how the object scatters incoming waves. In order to collect information, sensors are put in different locations to send and receive waves from each other. The choice of sensor positions and incident wave frequencies determines the reconstruction quality of scatterer properties. This paper introduces reinforcement learning to develop precision imaging that decides sensor positions and wave frequencies adaptive to different scatterers in an intelligent way, thus obtaining a significant improvement in reconstruction quality with limited imaging resources. Extensive numerical results will be provided to demonstrate the superiority of the proposed method over existing methods.