Learning When the Concept Shifts: Confounding, Invariance, and Dimension Reduction

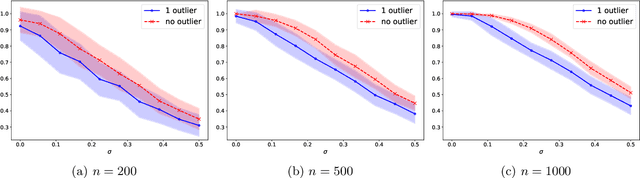
Practitioners often deploy a learned prediction model in a new environment where the joint distribution of covariate and response has shifted. In observational data, the distribution shift is often driven by unobserved confounding factors lurking in the environment, with the underlying mechanism unknown. Confounding can obfuscate the definition of the best prediction model (concept shift) and shift covariates to domains yet unseen (covariate shift). Therefore, a model maximizing prediction accuracy in the source environment could suffer a significant accuracy drop in the target environment. This motivates us to study the domain adaptation problem with observational data: given labeled covariate and response pairs from a source environment, and unlabeled covariates from a target environment, how can one predict the missing target response reliably? We root the adaptation problem in a linear structural causal model to address endogeneity and unobserved confounding. We study the necessity and benefit of leveraging exogenous, invariant covariate representations to cure concept shifts and improve target prediction. This further motivates a new representation learning method for adaptation that optimizes for a lower-dimensional linear subspace and, subsequently, a prediction model confined to that subspace. The procedure operates on a non-convex objective-that naturally interpolates between predictability and stability/invariance-constrained on the Stiefel manifold. We study the optimization landscape and prove that, when the regularization is sufficient, nearly all local optima align with an invariant linear subspace resilient to both concept and covariate shift. In terms of predictability, we show a model that uses the learned lower-dimensional subspace can incur a nearly ideal gap between target and source risk. Three real-world data sets are investigated to validate our method and theory.

Matching via Distance Profiles

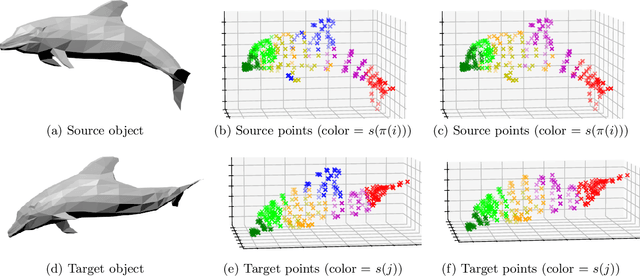
In this paper, we introduce and study matching methods based on distance profiles. For the matching of point clouds, the proposed method is easily implementable by solving a linear program, circumventing the computational obstacles of quadratic matching. Also, we propose and analyze a flexible way to execute location-to-location matching using distance profiles. Moreover, we provide a statistical estimation error analysis in the context of location-to-location matching using empirical process theory. Furthermore, we apply our method to a certain model and show its noise stability by characterizing conditions on the noise level for the matching to be successful. Lastly, we demonstrate the performance of the proposed method and compare it with some existing methods using synthetic and real data.

Online Learning to Transport via the Minimal Selection Principle

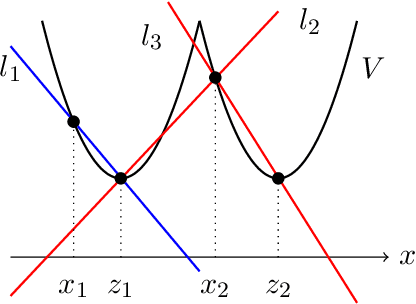
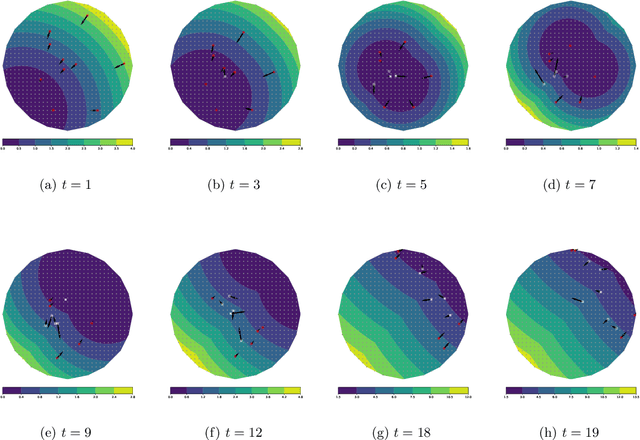
Motivated by robust dynamic resource allocation in operations research, we study the Online Learning to Transport (OLT) problem where the decision variable is a probability measure, an infinite-dimensional object. We draw connections between online learning, optimal transport, and partial differential equations through an insight called the minimal selection principle, originally studied in the Wasserstein gradient flow setting by Ambrosio et al. (2005). This allows us to extend the standard online learning framework to the infinite-dimensional setting seamlessly. Based on our framework, we derive a novel method called the minimal selection or exploration (MSoE) algorithm to solve OLT problems using mean-field approximation and discretization techniques. In the displacement convex setting, the main theoretical message underpinning our approach is that minimizing transport cost over time (via the minimal selection principle) ensures optimal cumulative regret upper bounds. On the algorithmic side, our MSoE algorithm applies beyond the displacement convex setting, making the mathematical theory of optimal transport practically relevant to non-convex settings common in dynamic resource allocation.

Reversible Gromov-Monge Sampler for Simulation-Based Inference

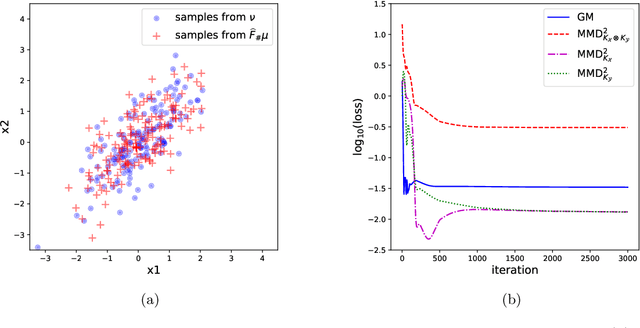
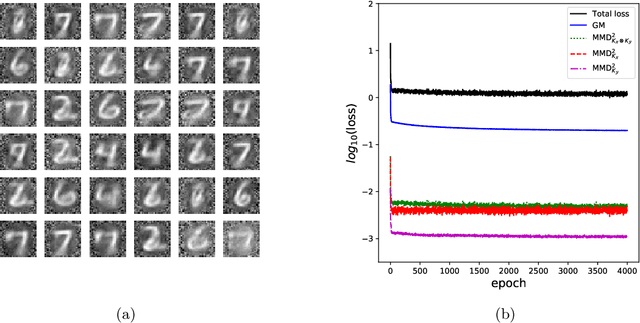
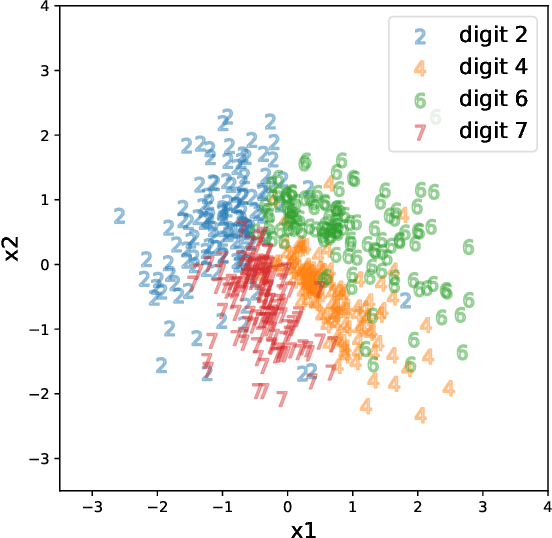
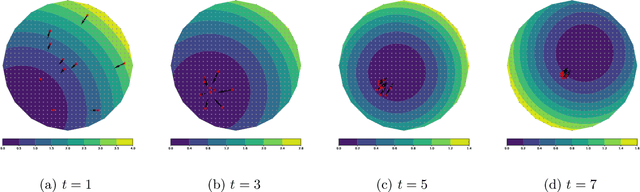
This paper introduces a new simulation-based inference procedure to model and sample from multi-dimensional probability distributions given access to i.i.d. samples, circumventing usual approaches of explicitly modeling the density function or designing Markov chain Monte Carlo. Motivated by the seminal work of M\'emoli (2011) and Sturm (2012) on distance and isomorphism between metric measure spaces, we propose a new notion called the Reversible Gromov-Monge (RGM) distance and study how RGM can be used to design new transform samplers in order to perform simulation-based inference. Our RGM sampler can also estimate optimal alignments between two heterogenous metric measure spaces $(\mathcal{X}, \mu, c_{\mathcal{X}})$ and $(\mathcal{Y}, \nu, c_{\mathcal{Y}})$ from empirical data sets, with estimated maps that approximately push forward one measure $\mu$ to the other $\nu$, and vice versa. Analytic properties of RGM distance are derived; statistical rate of convergence, representation, and optimization questions regarding the induced sampler are studied. Synthetic and real-world examples showcasing the effectiveness of the RGM sampler are also demonstrated.