Distributional Shrinkage II: Optimal Transport Denoisers with Higher-Order Scores

We revisit the signal denoising problem through the lens of optimal transport: the goal is to recover an unknown scalar signal distribution $X \sim P$ from noisy observations $Y = X + σZ$, with $Z$ being standard Gaussian independent of $X$ and $σ>0$ a known noise level. Let $Q$ denote the distribution of $Y$. We introduce a hierarchy of denoisers $T_0, T_1, \ldots, T_\infty : \mathbb{R} \to \mathbb{R}$ that are agnostic to the signal distribution $P$, depending only on higher-order score functions of $Q$. Each denoiser $T_K$ is progressively refined using the $(2K-1)$-th order score function of $Q$ at noise resolution $σ^{2K}$, achieving better denoising quality measured by the Wasserstein metric $W(T_K \sharp Q, P)$. The limiting denoiser $T_\infty$ identifies the optimal transport map with $T_\infty \sharp Q = P$. We provide a complete characterization of the combinatorial structure underlying this hierarchy through Bell polynomial recursions, revealing how higher-order score functions encode the optimal transport map for signal denoising. We study two estimation strategies with convergence rates for higher-order scores from i.i.d. samples drawn from $Q$: (i) plug-in estimation via Gaussian kernel smoothing, and (ii) direct estimation via higher-order score matching. This hierarchy of agnostic denoisers opens new perspectives in signal denoising and empirical Bayes.

Distributional Shrinkage I: Universal Denoisers in Multi-Dimensions

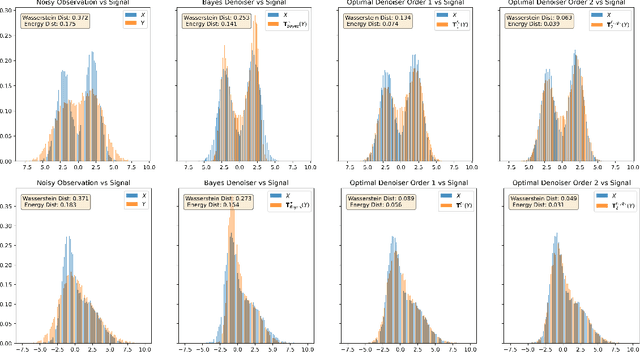
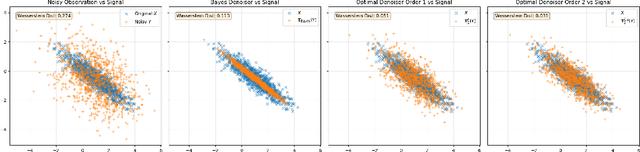
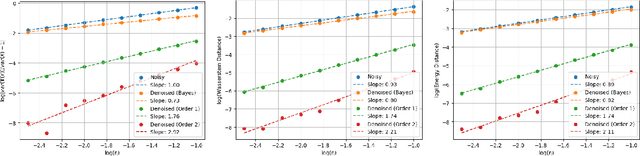
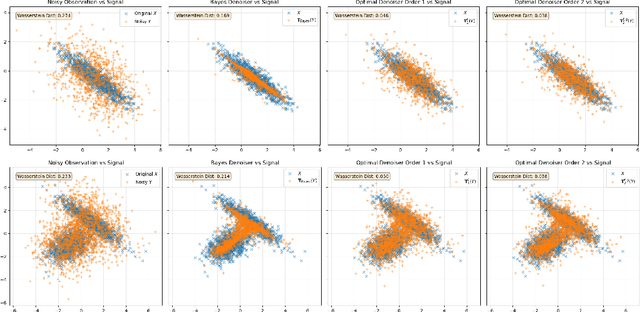
We revisit the problem of denoising from noisy measurements where only the noise level is known, not the noise distribution. In multi-dimensions, independent noise $Z$ corrupts the signal $X$, resulting in the noisy measurement $Y = X + σZ$, where $σ\in (0, 1)$ is a known noise level. Our goal is to recover the underlying signal distribution $P_X$ from denoising $P_Y$. We propose and analyze universal denoisers that are agnostic to a wide range of signal and noise distributions. Our distributional denoisers offer order-of-magnitude improvements over the Bayes-optimal denoiser derived from Tweedie's formula, if the focus is on the entire distribution $P_X$ rather than on individual realizations of $X$. Our denoisers shrink $P_Y$ toward $P_X$ optimally, achieving $O(σ^4)$ and $O(σ^6)$ accuracy in matching generalized moments and density functions. Inspired by optimal transport theory, the proposed denoisers are optimal in approximating the Monge-Ampère equation with higher-order accuracy, and can be implemented efficiently via score matching. Let $q$ represent the density of $P_Y$; for optimal distributional denoising, we recommend replacing the Bayes-optimal denoiser, \[ \mathbf{T}^*(y) = y + σ^2 \nabla \log q(y), \] with denoisers exhibiting less aggressive distributional shrinkage, \[ \mathbf{T}_1(y) = y + \frac{σ^2}{2} \nabla \log q(y), \] \[ \mathbf{T}_2(y) = y + \frac{σ^2}{2} \nabla \log q(y) - \frac{σ^4}{8} \nabla \left( \frac{1}{2} \| \nabla \log q(y) \|^2 + \nabla \cdot \nabla \log q(y) \right) . \]

No-Regret Generative Modeling via Parabolic Monge-Ampère PDE

We introduce a novel generative modeling framework based on a discretized parabolic Monge-Amp\`ere PDE, which emerges as a continuous limit of the Sinkhorn algorithm commonly used in optimal transport. Our method performs iterative refinement in the space of Brenier maps using a mirror gradient descent step. We establish theoretical guarantees for generative modeling through the lens of no-regret analysis, demonstrating that the iterates converge to the optimal Brenier map under a variety of step-size schedules. As a technical contribution, we derive a new Evolution Variational Inequality tailored to the parabolic Monge-Amp\`ere PDE, connecting geometry, transportation cost, and regret. Our framework accommodates non-log-concave target distributions, constructs an optimal sampling process via the Brenier map, and integrates favorable learning techniques from generative adversarial networks and score-based diffusion models. As direct applications, we illustrate how our theory paves new pathways for generative modeling and variational inference.

Denoising Diffusions with Optimal Transport: Localization, Curvature, and Multi-Scale Complexity

Adding noise is easy; what about denoising? Diffusion is easy; what about reverting a diffusion? Diffusion-based generative models aim to denoise a Langevin diffusion chain, moving from a log-concave equilibrium measure $\nu$, say isotropic Gaussian, back to a complex, possibly non-log-concave initial measure $\mu$. The score function performs denoising, going backward in time, predicting the conditional mean of the past location given the current. We show that score denoising is the optimal backward map in transportation cost. What is its localization uncertainty? We show that the curvature function determines this localization uncertainty, measured as the conditional variance of the past location given the current. We study in this paper the effectiveness of the diffuse-then-denoise process: the contraction of the forward diffusion chain, offset by the possible expansion of the backward denoising chain, governs the denoising difficulty. For any initial measure $\mu$, we prove that this offset net contraction at time $t$ is characterized by the curvature complexity of a smoothed $\mu$ at a specific signal-to-noise ratio (SNR) scale $r(t)$. We discover that the multi-scale curvature complexity collectively determines the difficulty of the denoising chain. Our multi-scale complexity quantifies a fine-grained notion of average-case curvature instead of the worst-case. Curiously, it depends on an integrated tail function, measuring the relative mass of locations with positive curvature versus those with negative curvature; denoising at a specific SNR scale is easy if such an integrated tail is light. We conclude with several non-log-concave examples to demonstrate how the multi-scale complexity probes the bottleneck SNR for the diffuse-then-denoise process.

Learning When the Concept Shifts: Confounding, Invariance, and Dimension Reduction

Practitioners often deploy a learned prediction model in a new environment where the joint distribution of covariate and response has shifted. In observational data, the distribution shift is often driven by unobserved confounding factors lurking in the environment, with the underlying mechanism unknown. Confounding can obfuscate the definition of the best prediction model (concept shift) and shift covariates to domains yet unseen (covariate shift). Therefore, a model maximizing prediction accuracy in the source environment could suffer a significant accuracy drop in the target environment. This motivates us to study the domain adaptation problem with observational data: given labeled covariate and response pairs from a source environment, and unlabeled covariates from a target environment, how can one predict the missing target response reliably? We root the adaptation problem in a linear structural causal model to address endogeneity and unobserved confounding. We study the necessity and benefit of leveraging exogenous, invariant covariate representations to cure concept shifts and improve target prediction. This further motivates a new representation learning method for adaptation that optimizes for a lower-dimensional linear subspace and, subsequently, a prediction model confined to that subspace. The procedure operates on a non-convex objective-that naturally interpolates between predictability and stability/invariance-constrained on the Stiefel manifold. We study the optimization landscape and prove that, when the regularization is sufficient, nearly all local optima align with an invariant linear subspace resilient to both concept and covariate shift. In terms of predictability, we show a model that uses the learned lower-dimensional subspace can incur a nearly ideal gap between target and source risk. Three real-world data sets are investigated to validate our method and theory.

Blessings and Curses of Covariate Shifts: Adversarial Learning Dynamics, Directional Convergence, and Equilibria

Covariate distribution shifts and adversarial perturbations present robustness challenges to the conventional statistical learning framework: seemingly small unconceivable shifts in the test covariate distribution can significantly affect the performance of the statistical model learned based on the training distribution. The model performance typically deteriorates when extrapolation happens: namely, covariates shift to a region where the training distribution is scarce, and naturally, the learned model has little information. For robustness and regularization considerations, adversarial perturbation techniques are proposed as a remedy; however, more needs to be studied about what extrapolation region adversarial covariate shift will focus on, given a learned model. This paper precisely characterizes the extrapolation region, examining both regression and classification in an infinite-dimensional setting. We study the implications of adversarial covariate shifts to subsequent learning of the equilibrium -- the Bayes optimal model -- in a sequential game framework. We exploit the dynamics of the adversarial learning game and reveal the curious effects of the covariate shift to equilibrium learning and experimental design. In particular, we establish two directional convergence results that exhibit distinctive phenomena: (1) a blessing in regression, the adversarial covariate shifts in an exponential rate to an optimal experimental design for rapid subsequent learning, (2) a curse in classification, the adversarial covariate shifts in a subquadratic rate fast to the hardest experimental design trapping subsequent learning.

High-dimensional Asymptotics of Langevin Dynamics in Spiked Matrix Models

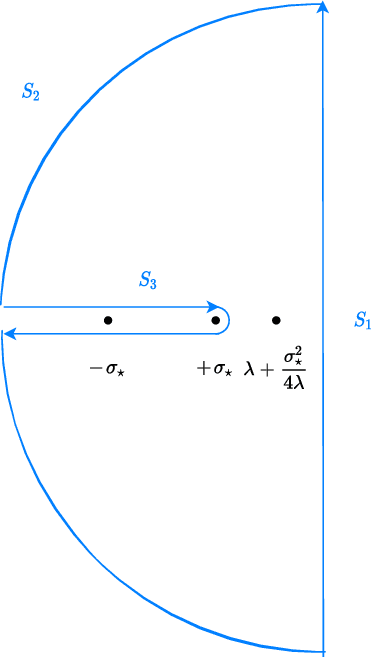
We study Langevin dynamics for recovering the planted signal in the spiked matrix model. We provide a "path-wise" characterization of the overlap between the output of the Langevin algorithm and the planted signal. This overlap is characterized in terms of a self-consistent system of integro-differential equations, usually referred to as the Crisanti-Horner-Sommers-Cugliandolo-Kurchan (CHSCK) equations in the spin glass literature. As a second contribution, we derive an explicit formula for the limiting overlap in terms of the signal-to-noise ratio and the injected noise in the diffusion. This uncovers a sharp phase transition -- in one regime, the limiting overlap is strictly positive, while in the other, the injected noise overcomes the signal, and the limiting overlap is zero.

Online Learning to Transport via the Minimal Selection Principle

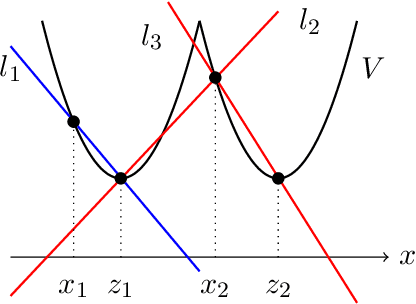
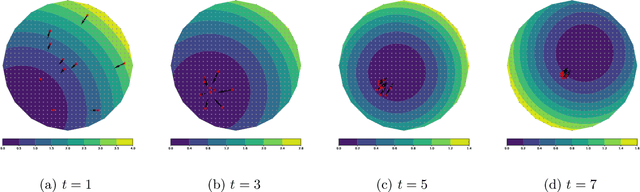
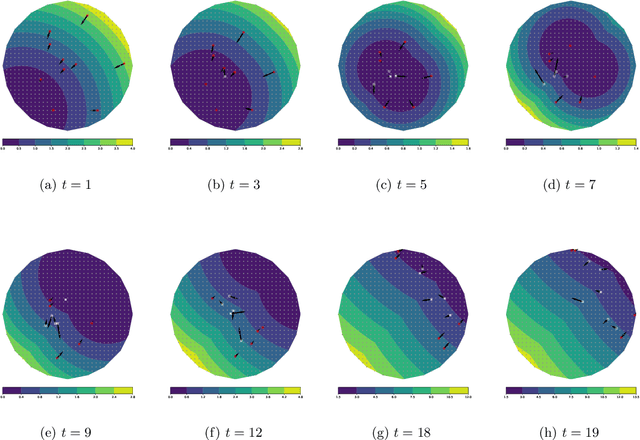
Motivated by robust dynamic resource allocation in operations research, we study the Online Learning to Transport (OLT) problem where the decision variable is a probability measure, an infinite-dimensional object. We draw connections between online learning, optimal transport, and partial differential equations through an insight called the minimal selection principle, originally studied in the Wasserstein gradient flow setting by Ambrosio et al. (2005). This allows us to extend the standard online learning framework to the infinite-dimensional setting seamlessly. Based on our framework, we derive a novel method called the minimal selection or exploration (MSoE) algorithm to solve OLT problems using mean-field approximation and discretization techniques. In the displacement convex setting, the main theoretical message underpinning our approach is that minimizing transport cost over time (via the minimal selection principle) ensures optimal cumulative regret upper bounds. On the algorithmic side, our MSoE algorithm applies beyond the displacement convex setting, making the mathematical theory of optimal transport practically relevant to non-convex settings common in dynamic resource allocation.

Reversible Gromov-Monge Sampler for Simulation-Based Inference

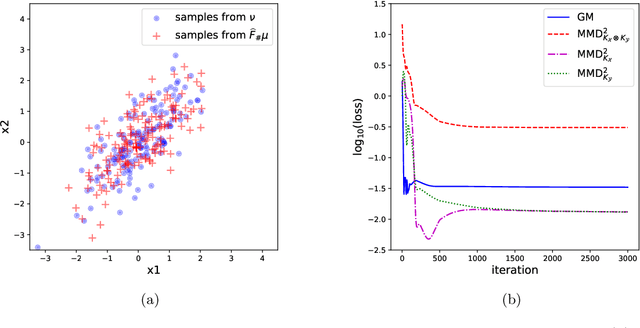
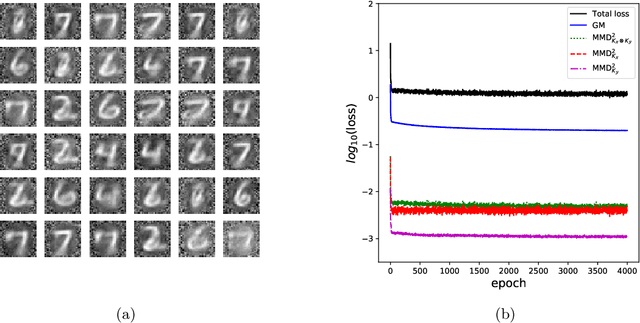
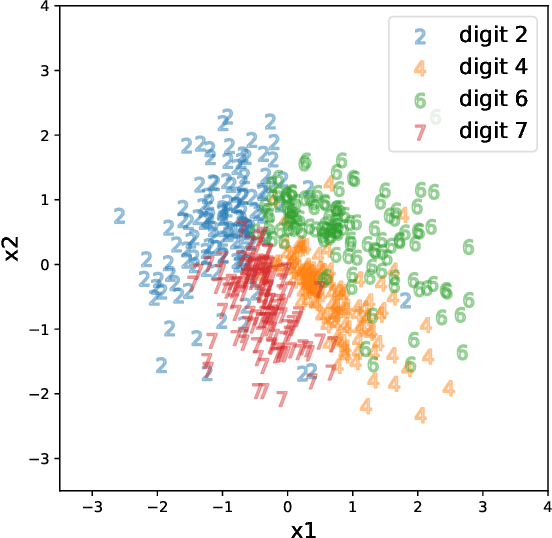
This paper introduces a new simulation-based inference procedure to model and sample from multi-dimensional probability distributions given access to i.i.d. samples, circumventing usual approaches of explicitly modeling the density function or designing Markov chain Monte Carlo. Motivated by the seminal work of M\'emoli (2011) and Sturm (2012) on distance and isomorphism between metric measure spaces, we propose a new notion called the Reversible Gromov-Monge (RGM) distance and study how RGM can be used to design new transform samplers in order to perform simulation-based inference. Our RGM sampler can also estimate optimal alignments between two heterogenous metric measure spaces $(\mathcal{X}, \mu, c_{\mathcal{X}})$ and $(\mathcal{Y}, \nu, c_{\mathcal{Y}})$ from empirical data sets, with estimated maps that approximately push forward one measure $\mu$ to the other $\nu$, and vice versa. Analytic properties of RGM distance are derived; statistical rate of convergence, representation, and optimization questions regarding the induced sampler are studied. Synthetic and real-world examples showcasing the effectiveness of the RGM sampler are also demonstrated.

Universal Prediction Band via Semi-Definite Programming

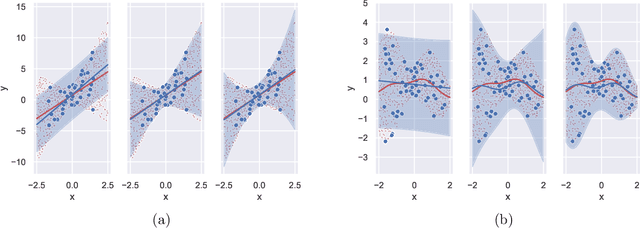
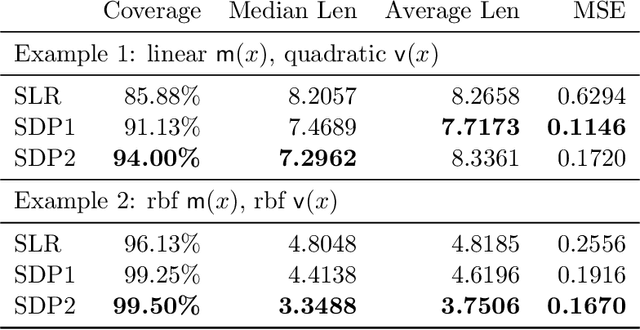
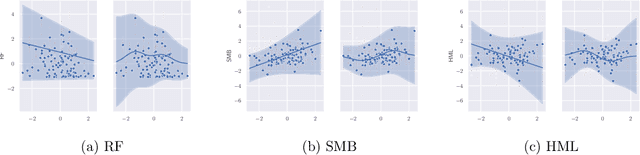
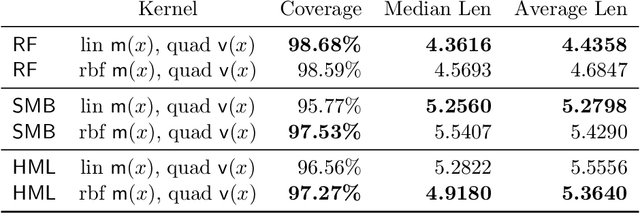
We propose a computationally efficient method to construct nonparametric, heteroskedastic prediction bands for uncertainty quantification, with or without any user-specified predictive model. The data-adaptive prediction band is universally applicable with minimal distributional assumptions, with strong non-asymptotic coverage properties, and easy to implement using standard convex programs. Our approach can be viewed as a novel variance interpolation with confidence and further leverages techniques from semi-definite programming and sum-of-squares optimization. Theoretical and numerical performances for the proposed approach for uncertainty quantification are analyzed.