Deep Learning for Individual Heterogeneity

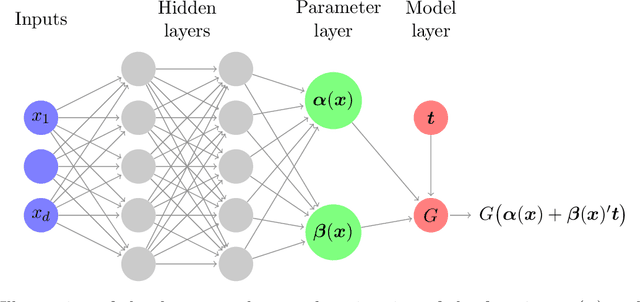
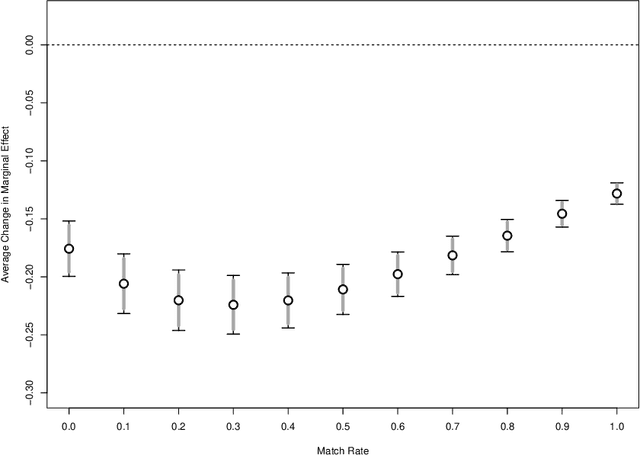
We propose a methodology for effectively modeling individual heterogeneity using deep learning while still retaining the interpretability and economic discipline of classical models. We pair a transparent, interpretable modeling structure with rich data environments and machine learning methods to estimate heterogeneous parameters based on potentially high dimensional or complex observable characteristics. Our framework is widely-applicable, covering numerous settings of economic interest. We recover, as special cases, well-known examples such as average treatment effects and parametric components of partially linear models. However, we also seamlessly deliver new results for diverse examples such as price elasticities, willingness-to-pay, and surplus measures in choice models, average marginal and partial effects of continuous treatment variables, fractional outcome models, count data, heterogeneous production function components, and more. Deep neural networks are well-suited to structured modeling of heterogeneity: we show how the network architecture can be designed to match the global structure of the economic model, giving novel methodology for deep learning as well as, more formally, improved rates of convergence. Our results on deep learning have consequences for other structured modeling environments and applications, such as for additive models. Our inference results are based on an influence function we derive, which we show to be flexible enough to to encompass all settings with a single, unified calculation, removing any requirement for case-by-case derivations. The usefulness of the methodology in economics is shown in two empirical applications: the response of 410(k) participation rates to firm matching and the impact of prices on subscription choices for an online service. Extensions to instrumental variables and multinomial choices are shown.

Deep Neural Networks for Estimation and Inference: Application to Causal Effects and Other Semiparametric Estimands

We study deep neural networks and their use in semiparametric inference. We provide new rates of convergence for deep feedforward neural nets and, because our rates are sufficiently fast (in some cases minimax optimal), prove that semiparametric inference is valid using deep nets for first-step estimation. Our estimation rates and semiparametric inference results are the first in the literature to handle the current standard architecture: fully connected feedforward neural networks (multi-layer perceptrons), with the now-default rectified linear unit (ReLU) activation function and a depth explicitly diverging with the sample size. We discuss other architectures as well, including fixed-width, very deep networks. We establish nonasymptotic bounds for these deep ReLU nets, for both least squares and logistic loses in nonparametric regression. We then apply our theory to develop semiparametric inference, focusing on treatment effects and expected profits for concreteness, and demonstrate their effectiveness with an empirical application to direct mail marketing. Inference in many other semiparametric contexts can be readily obtained.