Combining Particle and Tensor-network Methods for Partial Differential Equations via Sketching

In this paper, we propose a general framework for solving high-dimensional partial differential equations with tensor networks. Our approach offers a comprehensive solution methodology, wherein we employ a combination of particle simulations to update the solution and re-estimations of the new solution as a tensor-network using a recently proposed tensor train sketching technique. Our method can also be interpreted as an alternative approach for performing particle number control by assuming the particles originate from an underlying tensor network. We demonstrate the versatility and flexibility of our approach by applying it to two specific scenarios: simulating the Fokker-Planck equation through Langevin dynamics and quantum imaginary time evolution via auxiliary-field quantum Monte Carlo.

Generative Modeling via Hierarchical Tensor Sketching

We propose a hierarchical tensor-network approach for approximating high-dimensional probability density via empirical distribution. This leverages randomized singular value decomposition (SVD) techniques and involves solving linear equations for tensor cores in this tensor network. The complexity of the resulting algorithm scales linearly in the dimension of the high-dimensional density. An analysis of estimation error demonstrates the effectiveness of this method through several numerical experiments.

Automatic Melody Harmonization with Triad Chords: A Comparative Study

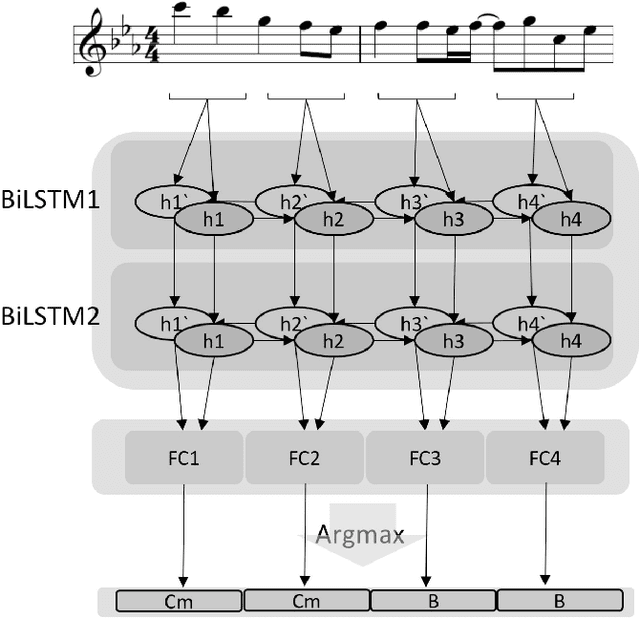
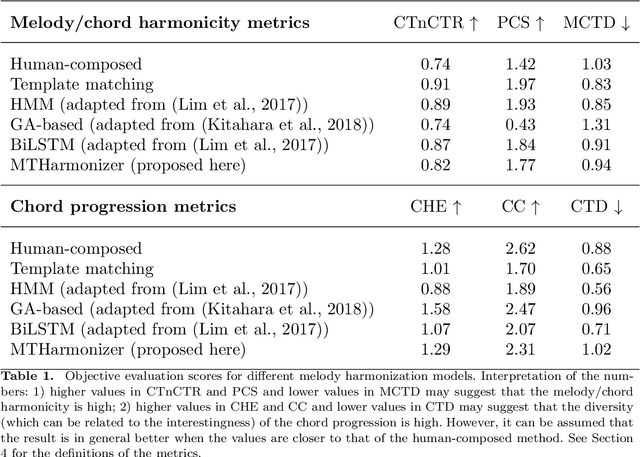
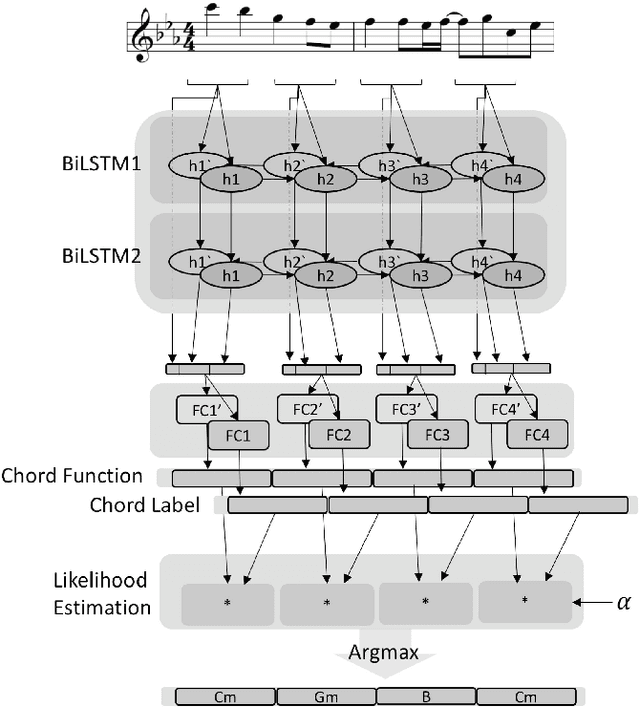
Several prior works have proposed various methods for the task of automatic melody harmonization, in which a model aims to generate a sequence of chords to serve as the harmonic accompaniment of a given multiple-bar melody sequence. In this paper, we present a comparative study evaluating and comparing the performance of a set of canonical approaches to this task, including a template matching based model, a hidden Markov based model, a genetic algorithm based model, and two deep learning based models. The evaluation is conducted on a dataset of 9,226 melody/chord pairs we newly collect for this study, considering up to 48 triad chords, using a standardized training/test split. We report the result of an objective evaluation using six different metrics and a subjective study with 202 participants.

Superhighway: Bypass Data Sparsity in Cross-Domain CF

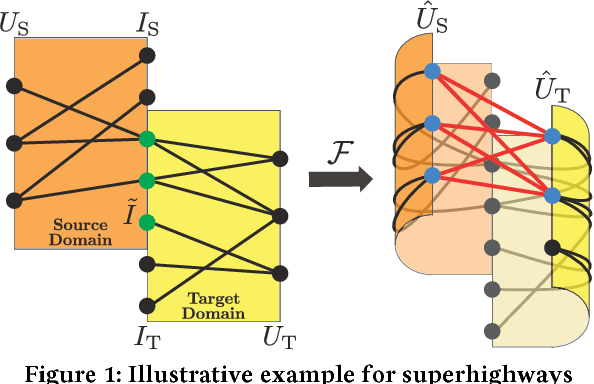
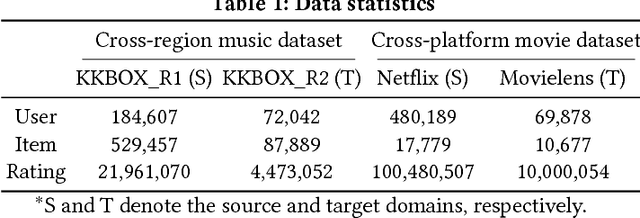
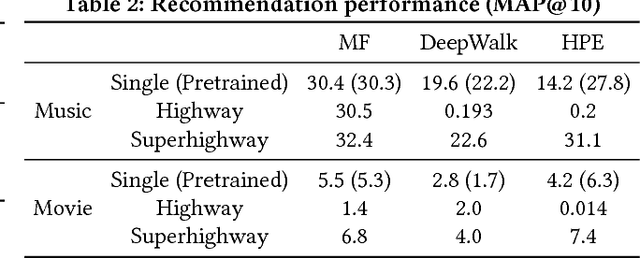
Cross-domain collaborative filtering (CF) aims to alleviate data sparsity in single-domain CF by leveraging knowledge transferred from related domains. Many traditional methods focus on enriching compared neighborhood relations in CF directly to address the sparsity problem. In this paper, we propose superhighway construction, an alternative explicit relation-enrichment procedure, to improve recommendations by enhancing cross-domain connectivity. Specifically, assuming partially overlapped items (users), superhighway bypasses multi-hop inter-domain paths between cross-domain users (items, respectively) with direct paths to enrich the cross-domain connectivity. The experiments conducted on a real-world cross-region music dataset and a cross-platform movie dataset show that the proposed superhighway construction significantly improves recommendation performance in both target and source domains.