Solving Inverse Problems via Diffusion-Based Priors: An Approximation-Free Ensemble Sampling Approach

Diffusion models (DMs) have proven to be effective in modeling high-dimensional distributions, leading to their widespread adoption for representing complex priors in Bayesian inverse problems (BIPs). However, current DM-based posterior sampling methods proposed for solving common BIPs rely on heuristic approximations to the generative process. To exploit the generative capability of DMs and avoid the usage of such approximations, we propose an ensemble-based algorithm that performs posterior sampling without the use of heuristic approximations. Our algorithm is motivated by existing works that combine DM-based methods with the sequential Monte Carlo (SMC) method. By examining how the prior evolves through the diffusion process encoded by the pre-trained score function, we derive a modified partial differential equation (PDE) governing the evolution of the corresponding posterior distribution. This PDE includes a modified diffusion term and a reweighting term, which can be simulated via stochastic weighted particle methods. Theoretically, we prove that the error between the true posterior distribution can be bounded in terms of the training error of the pre-trained score function and the number of particles in the ensemble. Empirically, we validate our algorithm on several inverse problems in imaging to show that our method gives more accurate reconstructions compared to existing DM-based methods.

A Unified Approach to Analysis and Design of Denoising Markov Models

Probabilistic generative models based on measure transport, such as diffusion and flow-based models, are often formulated in the language of Markovian stochastic dynamics, where the choice of the underlying process impacts both algorithmic design choices and theoretical analysis. In this paper, we aim to establish a rigorous mathematical foundation for denoising Markov models, a broad class of generative models that postulate a forward process transitioning from the target distribution to a simple, easy-to-sample distribution, alongside a backward process particularly constructed to enable efficient sampling in the reverse direction. Leveraging deep connections with nonequilibrium statistical mechanics and generalized Doob's $h$-transform, we propose a minimal set of assumptions that ensure: (1) explicit construction of the backward generator, (2) a unified variational objective directly minimizing the measure transport discrepancy, and (3) adaptations of the classical score-matching approach across diverse dynamics. Our framework unifies existing formulations of continuous and discrete diffusion models, identifies the most general form of denoising Markov models under certain regularity assumptions on forward generators, and provides a systematic recipe for designing denoising Markov models driven by arbitrary L\'evy-type processes. We illustrate the versatility and practical effectiveness of our approach through novel denoising Markov models employing geometric Brownian motion and jump processes as forward dynamics, highlighting the framework's potential flexibility and capability in modeling complex distributions.

HyperDPO: Hypernetwork-based Multi-Objective Fine-Tuning Framework

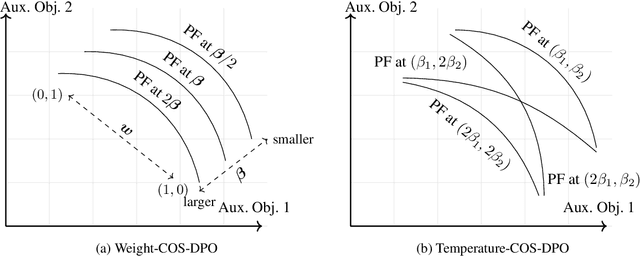
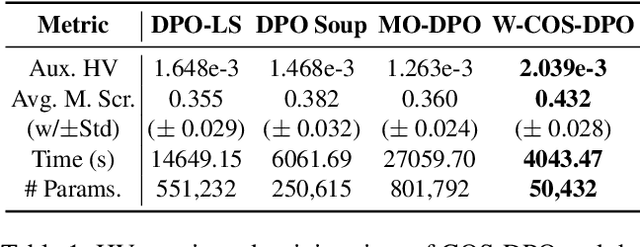
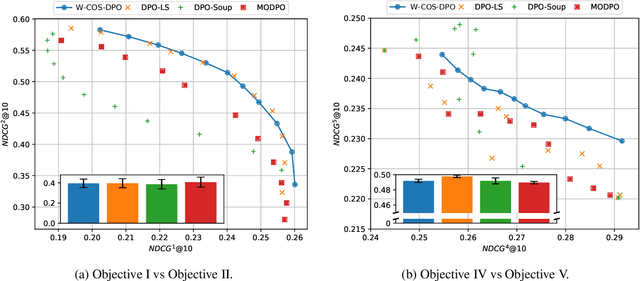
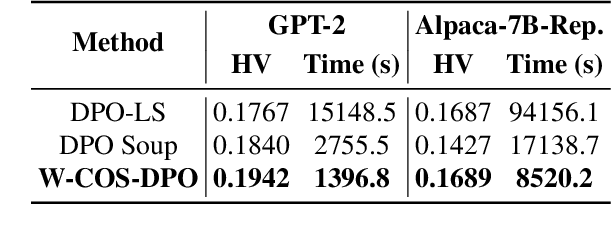
In LLM alignment and many other ML applications, one often faces the Multi-Objective Fine-Tuning (MOFT) problem, i.e. fine-tuning an existing model with datasets labeled w.r.t. different objectives simultaneously. To address the challenge, we propose the HyperDPO framework, a hypernetwork-based approach that extends the Direct Preference Optimization (DPO) technique, originally developed for efficient LLM alignment with preference data, to accommodate the MOFT settings. By substituting the Bradley-Terry-Luce model in DPO with the Plackett-Luce model, our framework is capable of handling a wide range of MOFT tasks that involve listwise ranking datasets. Compared with previous approaches, HyperDPO enjoys an efficient one-shot training process for profiling the Pareto front of auxiliary objectives, and offers flexible post-training control over trade-offs. Additionally, we propose a novel Hyper Prompt Tuning design, that conveys continuous weight across objectives to transformer-based models without altering their architecture. We demonstrate the effectiveness and efficiency of the HyperDPO framework through its applications to various tasks, including Learning-to-Rank (LTR) and LLM alignment, highlighting its viability for large-scale ML deployments.

How Discrete and Continuous Diffusion Meet: Comprehensive Analysis of Discrete Diffusion Models via a Stochastic Integral Framework

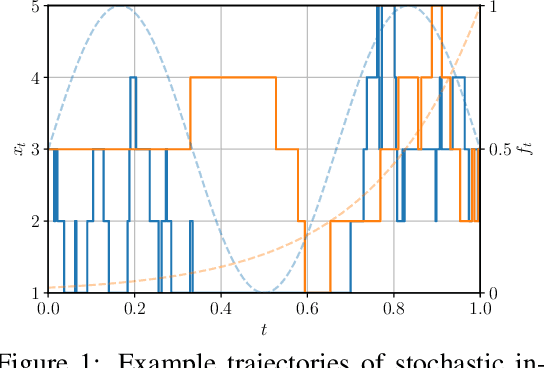
Discrete diffusion models have gained increasing attention for their ability to model complex distributions with tractable sampling and inference. However, the error analysis for discrete diffusion models remains less well-understood. In this work, we propose a comprehensive framework for the error analysis of discrete diffusion models based on L\'evy-type stochastic integrals. By generalizing the Poisson random measure to that with a time-independent and state-dependent intensity, we rigorously establish a stochastic integral formulation of discrete diffusion models and provide the corresponding change of measure theorems that are intriguingly analogous to It\^o integrals and Girsanov's theorem for their continuous counterparts. Our framework unifies and strengthens the current theoretical results on discrete diffusion models and obtains the first error bound for the $\tau$-leaping scheme in KL divergence. With error sources clearly identified, our analysis gives new insight into the mathematical properties of discrete diffusion models and offers guidance for the design of efficient and accurate algorithms for real-world discrete diffusion model applications.

Optimal starting point for time series forecasting

Recent advances on time series forecasting mainly focus on improving the forecasting models themselves. However, managing the length of the input data can also significantly enhance prediction performance. In this paper, we introduce a novel approach called Optimal Starting Point Time Series Forecast (OSP-TSP) to capture the intrinsic characteristics of time series data. By adjusting the sequence length via leveraging the XGBoost and LightGBM models, the proposed approach can determine optimal starting point (OSP) of the time series and thus enhance the prediction performances. The performances of the OSP-TSP approach are then evaluated across various frequencies on the M4 dataset and other real-world datasets. Empirical results indicate that predictions based on the OSP-TSP approach consistently outperform those using the complete dataset. Moreover, recognizing the necessity of sufficient data to effectively train models for OSP identification, we further propose targeted solutions to address the issue of data insufficiency.

Accelerating Diffusion Models with Parallel Sampling: Inference at Sub-Linear Time Complexity

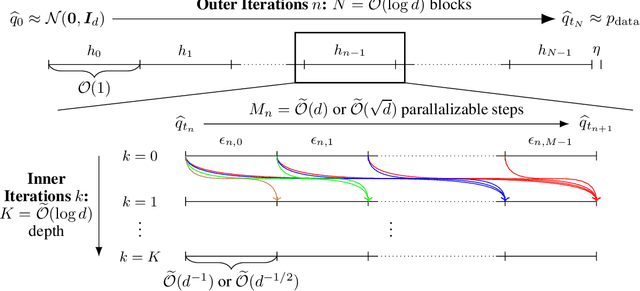
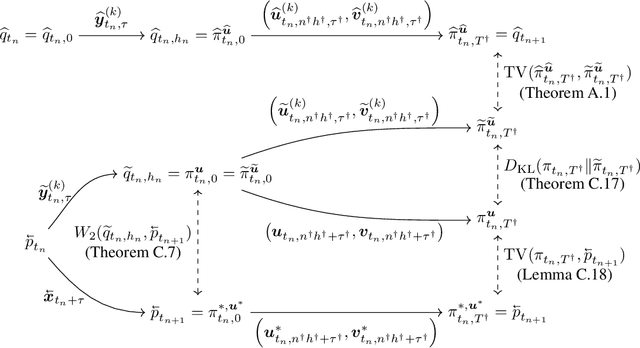
Diffusion models have become a leading method for generative modeling of both image and scientific data. As these models are costly to train and evaluate, reducing the inference cost for diffusion models remains a major goal. Inspired by the recent empirical success in accelerating diffusion models via the parallel sampling technique~\cite{shih2024parallel}, we propose to divide the sampling process into $\mathcal{O}(1)$ blocks with parallelizable Picard iterations within each block. Rigorous theoretical analysis reveals that our algorithm achieves $\widetilde{\mathcal{O}}(\mathrm{poly} \log d)$ overall time complexity, marking the first implementation with provable sub-linear complexity w.r.t. the data dimension $d$. Our analysis is based on a generalized version of Girsanov's theorem and is compatible with both the SDE and probability flow ODE implementations. Our results shed light on the potential of fast and efficient sampling of high-dimensional data on fast-evolving modern large-memory GPU clusters.

Understanding the Generalization Benefits of Late Learning Rate Decay

Why do neural networks trained with large learning rates for a longer time often lead to better generalization? In this paper, we delve into this question by examining the relation between training and testing loss in neural networks. Through visualization of these losses, we note that the training trajectory with a large learning rate navigates through the minima manifold of the training loss, finally nearing the neighborhood of the testing loss minimum. Motivated by these findings, we introduce a nonlinear model whose loss landscapes mirror those observed for real neural networks. Upon investigating the training process using SGD on our model, we demonstrate that an extended phase with a large learning rate steers our model towards the minimum norm solution of the training loss, which may achieve near-optimal generalization, thereby affirming the empirically observed benefits of late learning rate decay.

Statistical Spatially Inhomogeneous Diffusion Inference

Inferring a diffusion equation from discretely-observed measurements is a statistical challenge of significant importance in a variety of fields, from single-molecule tracking in biophysical systems to modeling financial instruments. Assuming that the underlying dynamical process obeys a $d$-dimensional stochastic differential equation of the form $$\mathrm{d}\boldsymbol{x}_t=\boldsymbol{b}(\boldsymbol{x}_t)\mathrm{d} t+\Sigma(\boldsymbol{x}_t)\mathrm{d}\boldsymbol{w}_t,$$ we propose neural network-based estimators of both the drift $\boldsymbol{b}$ and the spatially-inhomogeneous diffusion tensor $D = \Sigma\Sigma^{T}$ and provide statistical convergence guarantees when $\boldsymbol{b}$ and $D$ are $s$-H\"older continuous. Notably, our bound aligns with the minimax optimal rate $N^{-\frac{2s}{2s+d}}$ for nonparametric function estimation even in the presence of correlation within observational data, which necessitates careful handling when establishing fast-rate generalization bounds. Our theoretical results are bolstered by numerical experiments demonstrating accurate inference of spatially-inhomogeneous diffusion tensors.

Infinite forecast combinations based on Dirichlet process

Forecast combination integrates information from various sources by consolidating multiple forecast results from the target time series. Instead of the need to select a single optimal forecasting model, this paper introduces a deep learning ensemble forecasting model based on the Dirichlet process. Initially, the learning rate is sampled with three basis distributions as hyperparameters to convert the infinite mixture into a finite one. All checkpoints are collected to establish a deep learning sub-model pool, and weight adjustment and diversity strategies are developed during the combination process. The main advantage of this method is its ability to generate the required base learners through a single training process, utilizing the decaying strategy to tackle the challenge posed by the stochastic nature of gradient descent in determining the optimal learning rate. To ensure the method's generalizability and competitiveness, this paper conducts an empirical analysis using the weekly dataset from the M4 competition and explores sensitivity to the number of models to be combined. The results demonstrate that the ensemble model proposed offers substantial improvements in prediction accuracy and stability compared to a single benchmark model.

Multi-Objective Optimization via Wasserstein-Fisher-Rao Gradient Flow

Multi-objective optimization (MOO) aims to optimize multiple, possibly conflicting objectives with widespread applications. We introduce a novel interacting particle method for MOO inspired by molecular dynamics simulations. Our approach combines overdamped Langevin and birth-death dynamics, incorporating a "dominance potential" to steer particles toward global Pareto optimality. In contrast to previous methods, our method is able to relocate dominated particles, making it particularly adept at managing Pareto fronts of complicated geometries. Our method is also theoretically grounded as a Wasserstein-Fisher-Rao gradient flow with convergence guarantees. Extensive experiments confirm that our approach outperforms state-of-the-art methods on challenging synthetic and real-world datasets.