How Discrete and Continuous Diffusion Meet: Comprehensive Analysis of Discrete Diffusion Models via a Stochastic Integral Framework

Discrete diffusion models have gained increasing attention for their ability to model complex distributions with tractable sampling and inference. However, the error analysis for discrete diffusion models remains less well-understood. In this work, we propose a comprehensive framework for the error analysis of discrete diffusion models based on L\'evy-type stochastic integrals. By generalizing the Poisson random measure to that with a time-independent and state-dependent intensity, we rigorously establish a stochastic integral formulation of discrete diffusion models and provide the corresponding change of measure theorems that are intriguingly analogous to It\^o integrals and Girsanov's theorem for their continuous counterparts. Our framework unifies and strengthens the current theoretical results on discrete diffusion models and obtains the first error bound for the $\tau$-leaping scheme in KL divergence. With error sources clearly identified, our analysis gives new insight into the mathematical properties of discrete diffusion models and offers guidance for the design of efficient and accurate algorithms for real-world discrete diffusion model applications.

Accelerating Diffusion Models with Parallel Sampling: Inference at Sub-Linear Time Complexity

Diffusion models have become a leading method for generative modeling of both image and scientific data. As these models are costly to train and evaluate, reducing the inference cost for diffusion models remains a major goal. Inspired by the recent empirical success in accelerating diffusion models via the parallel sampling technique~\cite{shih2024parallel}, we propose to divide the sampling process into $\mathcal{O}(1)$ blocks with parallelizable Picard iterations within each block. Rigorous theoretical analysis reveals that our algorithm achieves $\widetilde{\mathcal{O}}(\mathrm{poly} \log d)$ overall time complexity, marking the first implementation with provable sub-linear complexity w.r.t. the data dimension $d$. Our analysis is based on a generalized version of Girsanov's theorem and is compatible with both the SDE and probability flow ODE implementations. Our results shed light on the potential of fast and efficient sampling of high-dimensional data on fast-evolving modern large-memory GPU clusters.

Ensemble-Based Annealed Importance Sampling

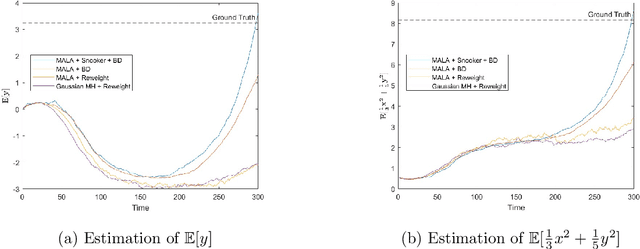
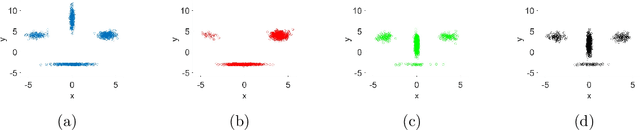
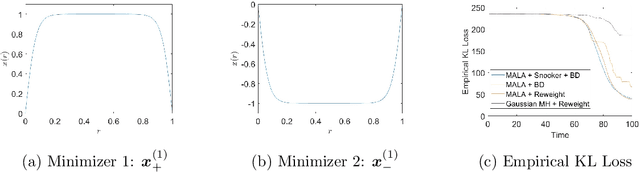
Sampling from a multimodal distribution is a fundamental and challenging problem in computational science and statistics. Among various approaches proposed for this task, one popular method is Annealed Importance Sampling (AIS). In this paper, we propose an ensemble-based version of AIS by combining it with population-based Monte Carlo methods to improve its efficiency. By keeping track of an ensemble instead of a single particle along some continuation path between the starting distribution and the target distribution, we take advantage of the interaction within the ensemble to encourage the exploration of undiscovered modes. Specifically, our main idea is to utilize either the snooker algorithm or the genetic algorithm used in Evolutionary Monte Carlo. We discuss how the proposed algorithm can be implemented and derive a partial differential equation governing the evolution of the ensemble under the continuous time and mean-field limit. We also test the efficiency of the proposed algorithm on various continuous and discrete distributions.

When can Regression-Adjusted Control Variates Help? Rare Events, Sobolev Embedding and Minimax Optimality

This paper studies the use of a machine learning-based estimator as a control variate for mitigating the variance of Monte Carlo sampling. Specifically, we seek to uncover the key factors that influence the efficiency of control variates in reducing variance. We examine a prototype estimation problem that involves simulating the moments of a Sobolev function based on observations obtained from (random) quadrature nodes. Firstly, we establish an information-theoretic lower bound for the problem. We then study a specific quadrature rule that employs a nonparametric regression-adjusted control variate to reduce the variance of the Monte Carlo simulation. We demonstrate that this kind of quadrature rule can improve the Monte Carlo rate and achieve the minimax optimal rate under a sufficient smoothness assumption. Due to the Sobolev Embedding Theorem, the sufficient smoothness assumption eliminates the existence of rare and extreme events. Finally, we show that, in the presence of rare and extreme events, a truncated version of the Monte Carlo algorithm can achieve the minimax optimal rate while the control variate cannot improve the convergence rate.

Physics-Informed Neural Operator for Learning Partial Differential Equations

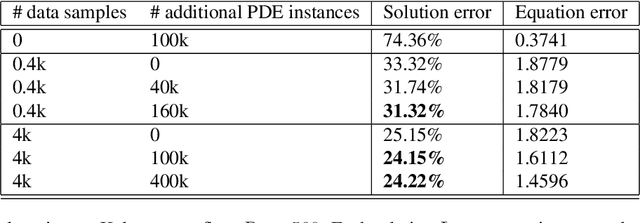
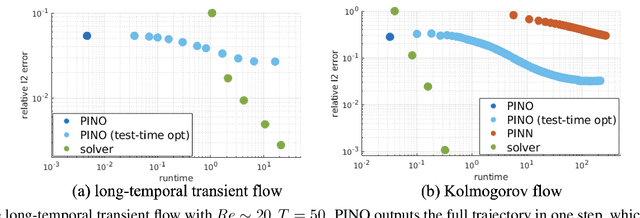
Machine learning methods have recently shown promise in solving partial differential equations (PDEs). They can be classified into two broad categories: approximating the solution function and learning the solution operator. The Physics-Informed Neural Network (PINN) is an example of the former while the Fourier neural operator (FNO) is an example of the latter. Both these approaches have shortcomings. The optimization in PINN is challenging and prone to failure, especially on multi-scale dynamic systems. FNO does not suffer from this optimization issue since it carries out supervised learning on a given dataset, but obtaining such data may be too expensive or infeasible. In this work, we propose the physics-informed neural operator (PINO), where we combine the operating-learning and function-optimization frameworks. This integrated approach improves convergence rates and accuracy over both PINN and FNO models. In the operator-learning phase, PINO learns the solution operator over multiple instances of the parametric PDE family. In the test-time optimization phase, PINO optimizes the pre-trained operator ansatz for the querying instance of the PDE. Experiments show PINO outperforms previous ML methods on many popular PDE families while retaining the extraordinary speed-up of FNO compared to solvers. In particular, PINO accurately solves challenging long temporal transient flows and Kolmogorov flows where other baseline ML methods fail to converge.

Machine Learning For Elliptic PDEs: Fast Rate Generalization Bound, Neural Scaling Law and Minimax Optimality

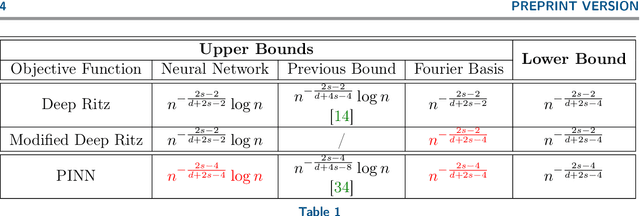
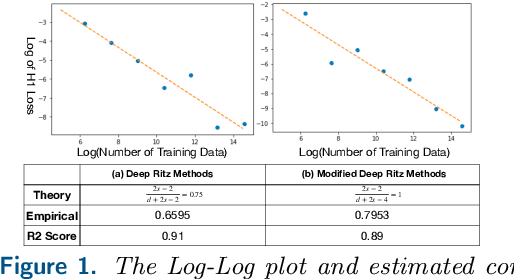
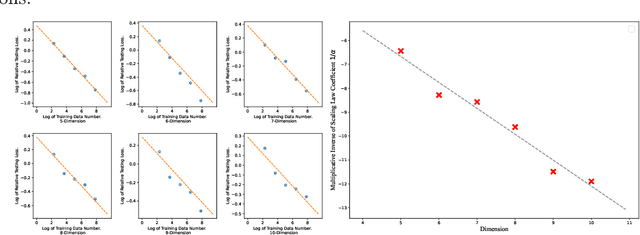
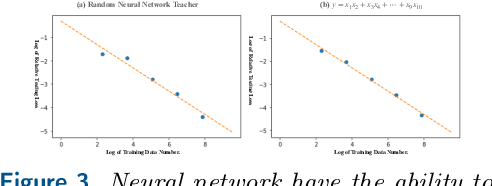
In this paper, we study the statistical limits of deep learning techniques for solving elliptic partial differential equations (PDEs) from random samples using the Deep Ritz Method (DRM) and Physics-Informed Neural Networks (PINNs). To simplify the problem, we focus on a prototype elliptic PDE: the Schr\"odinger equation on a hypercube with zero Dirichlet boundary condition, which has wide application in the quantum-mechanical systems. We establish upper and lower bounds for both methods, which improves upon concurrently developed upper bounds for this problem via a fast rate generalization bound. We discover that the current Deep Ritz Methods is sub-optimal and propose a modified version of it. We also prove that PINN and the modified version of DRM can achieve minimax optimal bounds over Sobolev spaces. Empirically, following recent work which has shown that the deep model accuracy will improve with growing training sets according to a power law, we supply computational experiments to show a similar behavior of dimension dependent power law for deep PDE solvers.