Features are fate: a theory of transfer learning in high-dimensional regression

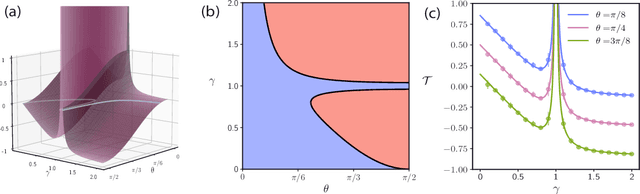
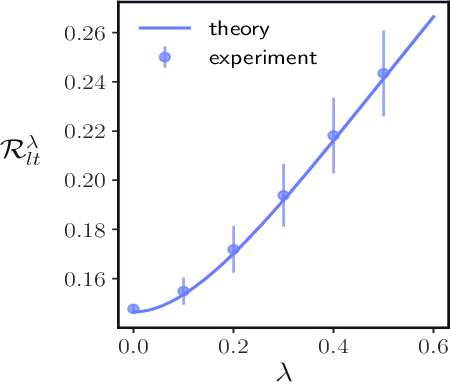
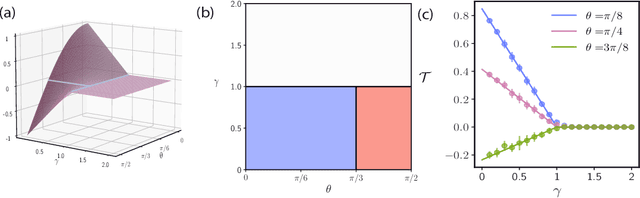
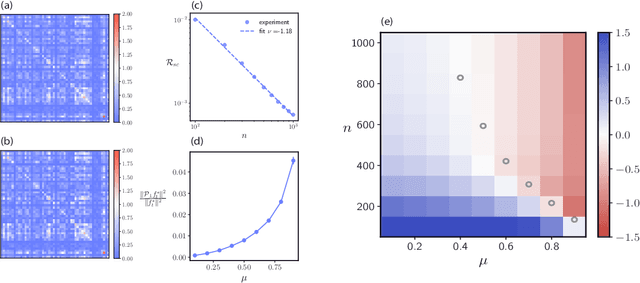
With the emergence of large-scale pre-trained neural networks, methods to adapt such "foundation" models to data-limited downstream tasks have become a necessity. Fine-tuning, preference optimization, and transfer learning have all been successfully employed for these purposes when the target task closely resembles the source task, but a precise theoretical understanding of "task similarity" is still lacking. While conventional wisdom suggests that simple measures of similarity between source and target distributions, such as $\phi$-divergences or integral probability metrics, can directly predict the success of transfer, we prove the surprising fact that, in general, this is not the case. We adopt, instead, a feature-centric viewpoint on transfer learning and establish a number of theoretical results that demonstrate that when the target task is well represented by the feature space of the pre-trained model, transfer learning outperforms training from scratch. We study deep linear networks as a minimal model of transfer learning in which we can analytically characterize the transferability phase diagram as a function of the target dataset size and the feature space overlap. For this model, we establish rigorously that when the feature space overlap between the source and target tasks is sufficiently strong, both linear transfer and fine-tuning improve performance, especially in the low data limit. These results build on an emerging understanding of feature learning dynamics in deep linear networks, and we demonstrate numerically that the rigorous results we derive for the linear case also apply to nonlinear networks.

How Discrete and Continuous Diffusion Meet: Comprehensive Analysis of Discrete Diffusion Models via a Stochastic Integral Framework

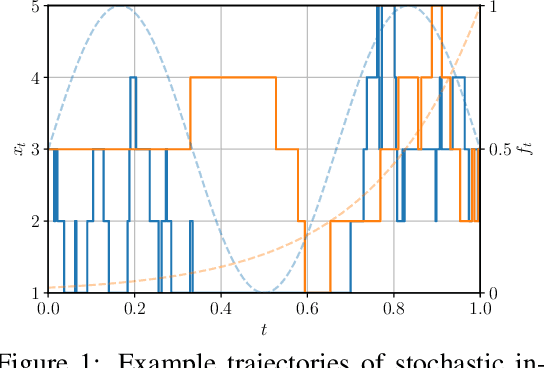
Discrete diffusion models have gained increasing attention for their ability to model complex distributions with tractable sampling and inference. However, the error analysis for discrete diffusion models remains less well-understood. In this work, we propose a comprehensive framework for the error analysis of discrete diffusion models based on L\'evy-type stochastic integrals. By generalizing the Poisson random measure to that with a time-independent and state-dependent intensity, we rigorously establish a stochastic integral formulation of discrete diffusion models and provide the corresponding change of measure theorems that are intriguingly analogous to It\^o integrals and Girsanov's theorem for their continuous counterparts. Our framework unifies and strengthens the current theoretical results on discrete diffusion models and obtains the first error bound for the $\tau$-leaping scheme in KL divergence. With error sources clearly identified, our analysis gives new insight into the mathematical properties of discrete diffusion models and offers guidance for the design of efficient and accurate algorithms for real-world discrete diffusion model applications.

Accurate and efficient structure elucidation from routine one-dimensional NMR spectra using multitask machine learning

Rapid determination of molecular structures can greatly accelerate workflows across many chemical disciplines. However, elucidating structure using only one-dimensional (1D) NMR spectra, the most readily accessible data, remains an extremely challenging problem because of the combinatorial explosion of the number of possible molecules as the number of constituent atoms is increased. Here, we introduce a multitask machine learning framework that predicts the molecular structure (formula and connectivity) of an unknown compound solely based on its 1D 1H and/or 13C NMR spectra. First, we show how a transformer architecture can be constructed to efficiently solve the task, traditionally performed by chemists, of assembling large numbers of molecular fragments into molecular structures. Integrating this capability with a convolutional neural network (CNN), we build an end-to-end model for predicting structure from spectra that is fast and accurate. We demonstrate the effectiveness of this framework on molecules with up to 19 heavy (non-hydrogen) atoms, a size for which there are trillions of possible structures. Without relying on any prior chemical knowledge such as the molecular formula, we show that our approach predicts the exact molecule 69.6% of the time within the first 15 predictions, reducing the search space by up to 11 orders of magnitude.

Accelerating Diffusion Models with Parallel Sampling: Inference at Sub-Linear Time Complexity

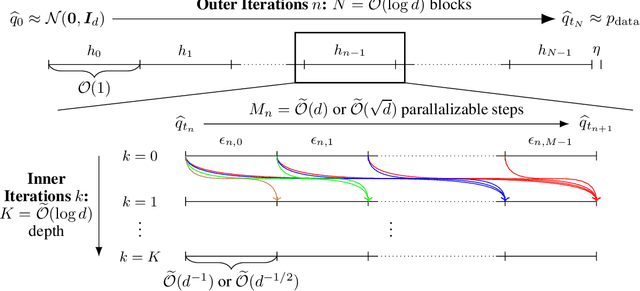
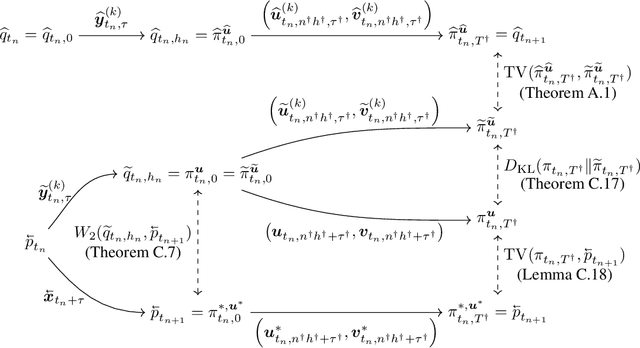
Diffusion models have become a leading method for generative modeling of both image and scientific data. As these models are costly to train and evaluate, reducing the inference cost for diffusion models remains a major goal. Inspired by the recent empirical success in accelerating diffusion models via the parallel sampling technique~\cite{shih2024parallel}, we propose to divide the sampling process into $\mathcal{O}(1)$ blocks with parallelizable Picard iterations within each block. Rigorous theoretical analysis reveals that our algorithm achieves $\widetilde{\mathcal{O}}(\mathrm{poly} \log d)$ overall time complexity, marking the first implementation with provable sub-linear complexity w.r.t. the data dimension $d$. Our analysis is based on a generalized version of Girsanov's theorem and is compatible with both the SDE and probability flow ODE implementations. Our results shed light on the potential of fast and efficient sampling of high-dimensional data on fast-evolving modern large-memory GPU clusters.

Energy Rank Alignment: Using Preference Optimization to Search Chemical Space at Scale

Searching through chemical space is an exceptionally challenging problem because the number of possible molecules grows combinatorially with the number of atoms. Large, autoregressive models trained on databases of chemical compounds have yielded powerful generators, but we still lack robust strategies for generating molecules with desired properties. This molecular search problem closely resembles the "alignment" problem for large language models, though for many chemical tasks we have a specific and easily evaluable reward function. Here, we introduce an algorithm called energy rank alignment (ERA) that leverages an explicit reward function to produce a gradient-based objective that we use to optimize autoregressive policies. We show theoretically that this algorithm is closely related to proximal policy optimization (PPO) and direct preference optimization (DPO), but has a minimizer that converges to an ideal Gibbs-Boltzmann distribution with the reward playing the role of an energy function. Furthermore, this algorithm is highly scalable, does not require reinforcement learning, and performs well relative to DPO when the number of preference observations per pairing is small. We deploy this approach to align molecular transformers to generate molecules with externally specified properties and find that it does so robustly, searching through diverse parts of chemical space. While our focus here is on chemical search, we also obtain excellent results on an AI supervised task for LLM alignment, showing that the method is scalable and general.

Statistical Spatially Inhomogeneous Diffusion Inference

Inferring a diffusion equation from discretely-observed measurements is a statistical challenge of significant importance in a variety of fields, from single-molecule tracking in biophysical systems to modeling financial instruments. Assuming that the underlying dynamical process obeys a $d$-dimensional stochastic differential equation of the form $$\mathrm{d}\boldsymbol{x}_t=\boldsymbol{b}(\boldsymbol{x}_t)\mathrm{d} t+\Sigma(\boldsymbol{x}_t)\mathrm{d}\boldsymbol{w}_t,$$ we propose neural network-based estimators of both the drift $\boldsymbol{b}$ and the spatially-inhomogeneous diffusion tensor $D = \Sigma\Sigma^{T}$ and provide statistical convergence guarantees when $\boldsymbol{b}$ and $D$ are $s$-H\"older continuous. Notably, our bound aligns with the minimax optimal rate $N^{-\frac{2s}{2s+d}}$ for nonparametric function estimation even in the presence of correlation within observational data, which necessitates careful handling when establishing fast-rate generalization bounds. Our theoretical results are bolstered by numerical experiments demonstrating accurate inference of spatially-inhomogeneous diffusion tensors.

Cooperative multi-agent reinforcement learning for high-dimensional nonequilibrium control

Experimental advances enabling high-resolution external control create new opportunities to produce materials with exotic properties. In this work, we investigate how a multi-agent reinforcement learning approach can be used to design external control protocols for self-assembly. We find that a fully decentralized approach performs remarkably well even with a "coarse" level of external control. More importantly, we see that a partially decentralized approach, where we include information about the local environment allows us to better control our system towards some target distribution. We explain this by analyzing our approach as a partially-observed Markov decision process. With a partially decentralized approach, the agent is able to act more presciently, both by preventing the formation of undesirable structures and by better stabilizing target structures as compared to a fully decentralized approach.

Efficient Bayesian Sampling Using Normalizing Flows to Assist Markov Chain Monte Carlo Methods

Normalizing flows can generate complex target distributions and thus show promise in many applications in Bayesian statistics as an alternative or complement to MCMC for sampling posteriors. Since no data set from the target posterior distribution is available beforehand, the flow is typically trained using the reverse Kullback-Leibler (KL) divergence that only requires samples from a base distribution. This strategy may perform poorly when the posterior is complicated and hard to sample with an untrained normalizing flow. Here we explore a distinct training strategy, using the direct KL divergence as loss, in which samples from the posterior are generated by (i) assisting a local MCMC algorithm on the posterior with a normalizing flow to accelerate its mixing rate and (ii) using the data generated this way to train the flow. The method only requires a limited amount of \textit{a~priori} input about the posterior, and can be used to estimate the evidence required for model validation, as we illustrate on examples.

A Dynamical Central Limit Theorem for Shallow Neural Networks

Recent theoretical work has characterized the dynamics of wide shallow neural networks trained via gradient descent in an asymptotic regime called the mean-field limit as the number of parameters tends towards infinity. At initialization, the randomly sampled parameters lead to a deviation from the mean-field limit that is dictated by the classical Central Limit Theorem (CLT). However, the dynamics of training introduces correlations among the parameters, raising the question of how the fluctuations evolve during training. Here, we analyze the mean-field dynamics as a Wasserstein gradient flow and prove that the deviations from the mean-field limit scaled by the width, in the width-asymptotic limit, remain bounded throughout training. In particular, they eventually vanish in the CLT scaling if the mean-field dynamics converges to a measure that interpolates the training data. This observation has implications for both the approximation rate and the generalization: the upper bound we obtain is given by a Monte-Carlo type resampling error, which does not depend explicitly on the dimension. This bound motivates a regularizaton term on the 2-norm of the underlying measure, which is also connected to generalization via the variation-norm function spaces.

Learning with rare data: Using active importance sampling to optimize objectives dominated by rare events

Deep neural networks, when optimized with sufficient data, provide accurate representations of high-dimensional functions; in contrast, function approximation techniques that have predominated in scientific computing do not scale well with dimensionality. As a result, many high-dimensional sampling and approximation problems once thought intractable are being revisited through the lens of machine learning. While the promise of unparalleled accuracy may suggest a renaissance for applications that require parameterizing representations of complex systems, in many applications gathering sufficient data to develop such a representation remains a significant challenge. Here we introduce an approach that combines rare events sampling techniques with neural network optimization to optimize objective functions that are dominated by rare events. We show that importance sampling reduces the asymptotic variance of the solution to a learning problem, suggesting benefits for generalization. We study our algorithm in the context of learning dynamical transition pathways between two states of a system, a problem with applications in statistical physics and implications in machine learning theory. Our numerical experiments demonstrate that we can successfully learn even with the compounding difficulties of high-dimension and rare data.