Improving the evaluation of samplers on multi-modal targets

Addressing multi-modality constitutes one of the major challenges of sampling. In this reflection paper, we advocate for a more systematic evaluation of samplers towards two sources of difficulty that are mode separation and dimension. For this, we propose a synthetic experimental setting that we illustrate on a selection of samplers, focusing on the challenging criterion of recovery of the mode relative importance. These evaluations are crucial to diagnose the potential of samplers to handle multi-modality and therefore to drive progress in the field.

Learned Reference-based Diffusion Sampling for multi-modal distributions

Over the past few years, several approaches utilizing score-based diffusion have been proposed to sample from probability distributions, that is without having access to exact samples and relying solely on evaluations of unnormalized densities. The resulting samplers approximate the time-reversal of a noising diffusion process, bridging the target distribution to an easy-to-sample base distribution. In practice, the performance of these methods heavily depends on key hyperparameters that require ground truth samples to be accurately tuned. Our work aims to highlight and address this fundamental issue, focusing in particular on multi-modal distributions, which pose significant challenges for existing sampling methods. Building on existing approaches, we introduce Learned Reference-based Diffusion Sampler (LRDS), a methodology specifically designed to leverage prior knowledge on the location of the target modes in order to bypass the obstacle of hyperparameter tuning. LRDS proceeds in two steps by (i) learning a reference diffusion model on samples located in high-density space regions and tailored for multimodality, and (ii) using this reference model to foster the training of a diffusion-based sampler. We experimentally demonstrate that LRDS best exploits prior knowledge on the target distribution compared to competing algorithms on a variety of challenging distributions.

A theoretical perspective on mode collapse in variational inference

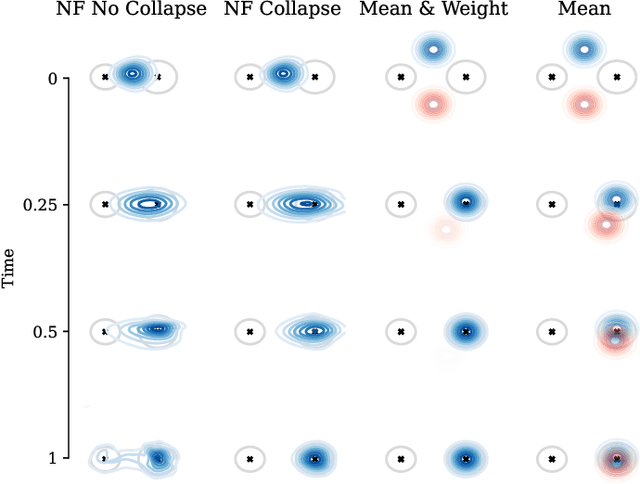
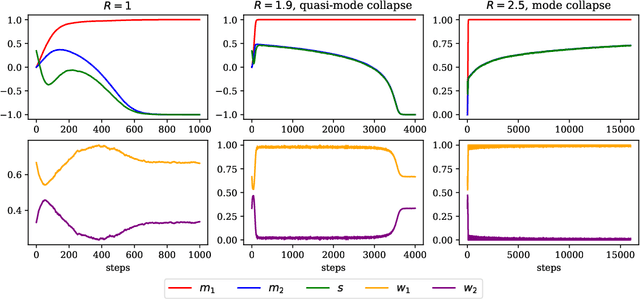
While deep learning has expanded the possibilities for highly expressive variational families, the practical benefits of these tools for variational inference (VI) are often limited by the minimization of the traditional Kullback-Leibler objective, which can yield suboptimal solutions. A major challenge in this context is \emph{mode collapse}: the phenomenon where a model concentrates on a few modes of the target distribution during training, despite being statistically capable of expressing them all. In this work, we carry a theoretical investigation of mode collapse for the gradient flow on Gaussian mixture models. We identify the key low-dimensional statistics characterizing the flow, and derive a closed set of low-dimensional equations governing their evolution. Leveraging this compact description, we show that mode collapse is present even in statistically favorable scenarios, and identify two key mechanisms driving it: mean alignment and vanishing weight. Our theoretical findings are consistent with the implementation of VI using normalizing flows, a class of popular generative models, thereby offering practical insights.

Stochastic Localization via Iterative Posterior Sampling

Building upon score-based learning, new interest in stochastic localization techniques has recently emerged. In these models, one seeks to noise a sample from the data distribution through a stochastic process, called observation process, and progressively learns a denoiser associated to this dynamics. Apart from specific applications, the use of stochastic localization for the problem of sampling from an unnormalized target density has not been explored extensively. This work contributes to fill this gap. We consider a general stochastic localization framework and introduce an explicit class of observation processes, associated with flexible denoising schedules. We provide a complete methodology, $\textit{Stochastic Localization via Iterative Posterior Sampling}$ (SLIPS), to obtain approximate samples of this dynamics, and as a by-product, samples from the target distribution. Our scheme is based on a Markov chain Monte Carlo estimation of the denoiser and comes with detailed practical guidelines. We illustrate the benefits and applicability of SLIPS on several benchmarks, including Gaussian mixtures in increasing dimensions, Bayesian logistic regression and a high-dimensional field system from statistical-mechanics.

Active learning of Boltzmann samplers and potential energies with quantum mechanical accuracy

Extracting consistent statistics between relevant free-energy minima of a molecular system is essential for physics, chemistry and biology. Molecular dynamics (MD) simulations can aid in this task but are computationally expensive, especially for systems that require quantum accuracy. To overcome this challenge, we develop an approach combining enhanced sampling with deep generative models and active learning of a machine learning potential (MLP). We introduce an adaptive Markov chain Monte Carlo framework that enables the training of one Normalizing Flow (NF) and one MLP per state. We simulate several Markov chains in parallel until they reach convergence, sampling the Boltzmann distribution with an efficient use of energy evaluations. At each iteration, we compute the energy of a subset of the NF-generated configurations using Density Functional Theory (DFT), we predict the remaining configuration's energy with the MLP and actively train the MLP using the DFT-computed energies. Leveraging the trained NF and MLP models, we can compute thermodynamic observables such as free-energy differences or optical spectra. We apply this method to study the isomerization of an ultrasmall silver nanocluster, belonging to a set of systems with diverse applications in the fields of medicine and catalysis.

Balanced Training of Energy-Based Models with Adaptive Flow Sampling

Energy-based models (EBMs) are versatile density estimation models that directly parameterize an unnormalized log density. Although very flexible, EBMs lack a specified normalization constant of the model, making the likelihood of the model computationally intractable. Several approximate samplers and variational inference techniques have been proposed to estimate the likelihood gradients for training. These techniques have shown promising results in generating samples, but little attention has been paid to the statistical accuracy of the estimated density, such as determining the relative importance of different classes in a dataset. In this work, we propose a new maximum likelihood training algorithm for EBMs that uses a different type of generative model, normalizing flows (NF), which have recently been proposed to facilitate sampling. Our method fits an NF to an EBM during training so that an NF-assisted sampling scheme provides an accurate gradient for the EBMs at all times, ultimately leading to a fast sampler for generating new data.

On Sampling with Approximate Transport Maps

Transport maps can ease the sampling of distributions with non-trivial geometries by transforming them into distributions that are easier to handle. The potential of this approach has risen with the development of Normalizing Flows (NF) which are maps parameterized with deep neural networks trained to push a reference distribution towards a target. NF-enhanced samplers recently proposed blend (Markov chain) Monte Carlo methods with either (i) proposal draws from the flow or (ii) a flow-based reparametrization. In both cases, the quality of the learned transport conditions performance. The present work clarifies for the first time the relative strengths and weaknesses of these two approaches. Our study concludes that multimodal targets can reliability be handled with flow-based proposals up to moderately high dimensions. In contrast, methods relying on reparametrization struggle with multimodality but are more robust otherwise in high-dimensional settings and under poor training. To further illustrate the influence of target-proposal adequacy, we also derive a new quantitative bound for the mixing time of the Independent Metropolis-Hastings sampler.

Efficient Bayesian Sampling Using Normalizing Flows to Assist Markov Chain Monte Carlo Methods

Normalizing flows can generate complex target distributions and thus show promise in many applications in Bayesian statistics as an alternative or complement to MCMC for sampling posteriors. Since no data set from the target posterior distribution is available beforehand, the flow is typically trained using the reverse Kullback-Leibler (KL) divergence that only requires samples from a base distribution. This strategy may perform poorly when the posterior is complicated and hard to sample with an untrained normalizing flow. Here we explore a distinct training strategy, using the direct KL divergence as loss, in which samples from the posterior are generated by (i) assisting a local MCMC algorithm on the posterior with a normalizing flow to accelerate its mixing rate and (ii) using the data generated this way to train the flow. The method only requires a limited amount of \textit{a~priori} input about the posterior, and can be used to estimate the evidence required for model validation, as we illustrate on examples.

Dual Training of Energy-Based Models with Overparametrized Shallow Neural Networks

Energy-based models (EBMs) are generative models that are usually trained via maximum likelihood estimation. This approach becomes challenging in generic situations where the trained energy is nonconvex, due to the need to sample the Gibbs distribution associated with this energy. Using general Fenchel duality results, we derive variational principles dual to maximum likelihood EBMs with shallow overparametrized neural network energies, both in the active (aka feature-learning) and lazy regimes. In the active regime, this dual formulation leads to a training algorithm in which one updates concurrently the particles in the sample space and the neurons in the parameter space of the energy. We also consider a variant of this algorithm in which the particles are sometimes restarted at random samples drawn from the data set, and show that performing these restarts at every iteration step corresponds to score matching training. Using intermediate parameter setups in our dual algorithm thereby gives a way to interpolate between maximum likelihood and score matching training. These results are illustrated in simple numerical experiments.

More data or more parameters? Investigating the effect of data structure on generalization

One of the central features of deep learning is the generalization abilities of neural networks, which seem to improve relentlessly with over-parametrization. In this work, we investigate how properties of data impact the test error as a function of the number of training examples and number of training parameters; in other words, how the structure of data shapes the "generalization phase space". We first focus on the random features model trained in the teacher-student scenario. The synthetic input data is composed of independent blocks, which allow us to tune the saliency of low-dimensional structures and their relevance with respect to the target function. Using methods from statistical physics, we obtain an analytical expression for the train and test errors for both regression and classification tasks in the high-dimensional limit. The derivation allows us to show that noise in the labels and strong anisotropy of the input data play similar roles on the test error. Both promote an asymmetry of the phase space where increasing the number of training examples improves generalization further than increasing the number of training parameters. Our analytical insights are confirmed by numerical experiments involving fully-connected networks trained on MNIST and CIFAR10.