A theoretical perspective on mode collapse in variational inference
Paper and Code
Oct 17, 2024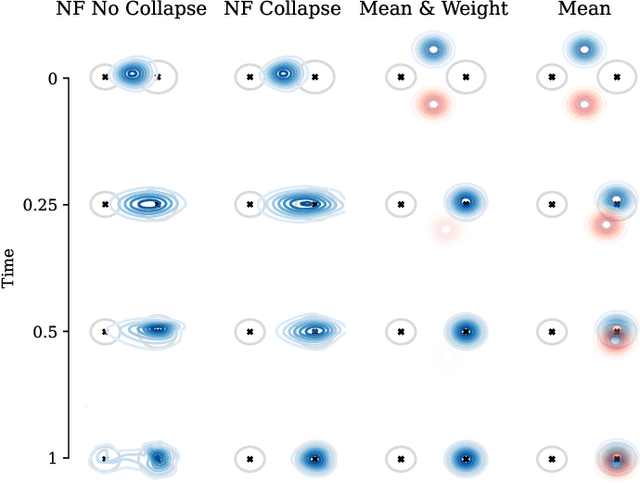

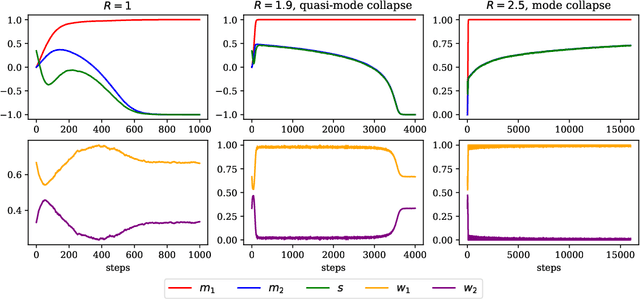

While deep learning has expanded the possibilities for highly expressive variational families, the practical benefits of these tools for variational inference (VI) are often limited by the minimization of the traditional Kullback-Leibler objective, which can yield suboptimal solutions. A major challenge in this context is \emph{mode collapse}: the phenomenon where a model concentrates on a few modes of the target distribution during training, despite being statistically capable of expressing them all. In this work, we carry a theoretical investigation of mode collapse for the gradient flow on Gaussian mixture models. We identify the key low-dimensional statistics characterizing the flow, and derive a closed set of low-dimensional equations governing their evolution. Leveraging this compact description, we show that mode collapse is present even in statistically favorable scenarios, and identify two key mechanisms driving it: mean alignment and vanishing weight. Our theoretical findings are consistent with the implementation of VI using normalizing flows, a class of popular generative models, thereby offering practical insights.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge