Features are fate: a theory of transfer learning in high-dimensional regression
Paper and Code
Oct 10, 2024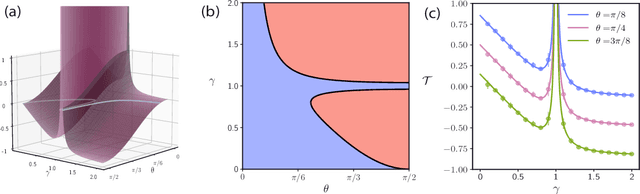
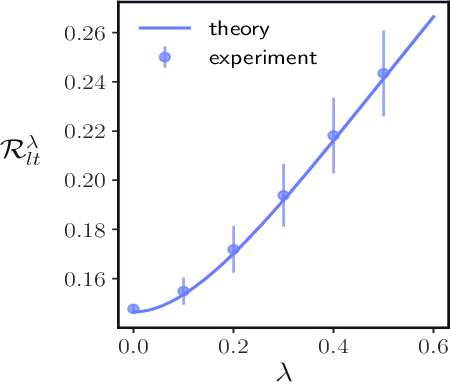
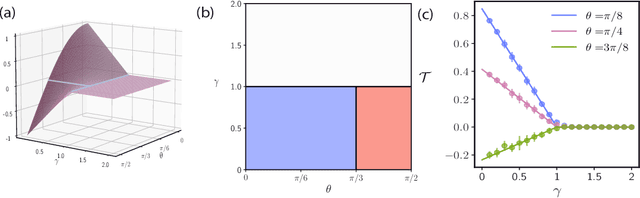
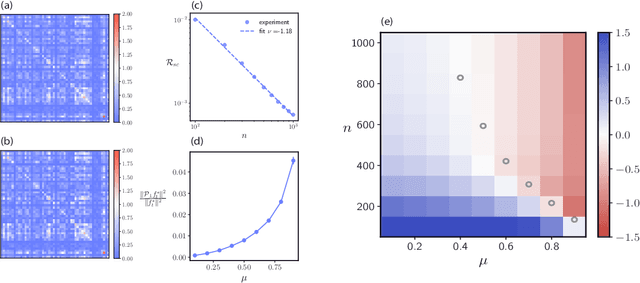
With the emergence of large-scale pre-trained neural networks, methods to adapt such "foundation" models to data-limited downstream tasks have become a necessity. Fine-tuning, preference optimization, and transfer learning have all been successfully employed for these purposes when the target task closely resembles the source task, but a precise theoretical understanding of "task similarity" is still lacking. While conventional wisdom suggests that simple measures of similarity between source and target distributions, such as $\phi$-divergences or integral probability metrics, can directly predict the success of transfer, we prove the surprising fact that, in general, this is not the case. We adopt, instead, a feature-centric viewpoint on transfer learning and establish a number of theoretical results that demonstrate that when the target task is well represented by the feature space of the pre-trained model, transfer learning outperforms training from scratch. We study deep linear networks as a minimal model of transfer learning in which we can analytically characterize the transferability phase diagram as a function of the target dataset size and the feature space overlap. For this model, we establish rigorously that when the feature space overlap between the source and target tasks is sufficiently strong, both linear transfer and fine-tuning improve performance, especially in the low data limit. These results build on an emerging understanding of feature learning dynamics in deep linear networks, and we demonstrate numerically that the rigorous results we derive for the linear case also apply to nonlinear networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge