Ensemble-Based Annealed Importance Sampling
Paper and Code
Jan 28, 2024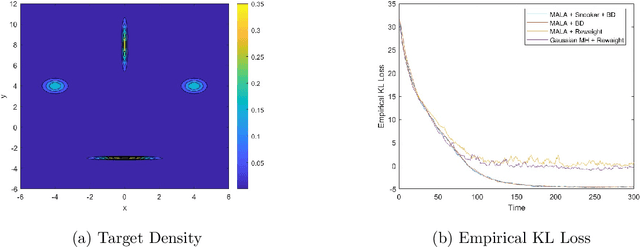
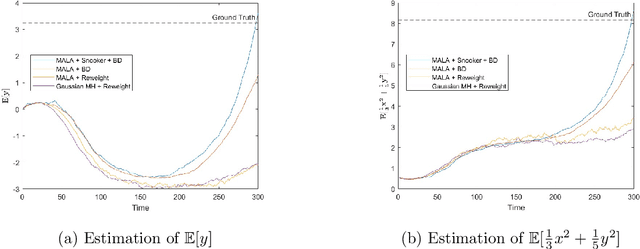
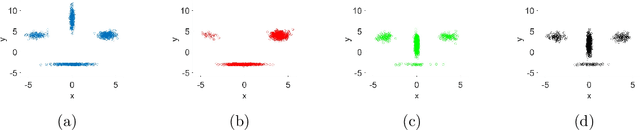
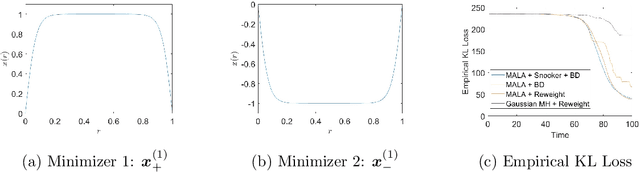
Sampling from a multimodal distribution is a fundamental and challenging problem in computational science and statistics. Among various approaches proposed for this task, one popular method is Annealed Importance Sampling (AIS). In this paper, we propose an ensemble-based version of AIS by combining it with population-based Monte Carlo methods to improve its efficiency. By keeping track of an ensemble instead of a single particle along some continuation path between the starting distribution and the target distribution, we take advantage of the interaction within the ensemble to encourage the exploration of undiscovered modes. Specifically, our main idea is to utilize either the snooker algorithm or the genetic algorithm used in Evolutionary Monte Carlo. We discuss how the proposed algorithm can be implemented and derive a partial differential equation governing the evolution of the ensemble under the continuous time and mean-field limit. We also test the efficiency of the proposed algorithm on various continuous and discrete distributions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge