Burigede Liu
Temperature-Aware Recurrent Neural Operator for Temperature-Dependent Anisotropic Plasticity in HCP Materials
Aug 26, 2025Abstract:Neural network surrogate models for constitutive laws in computational mechanics have been in use for some time. In plasticity, these models often rely on gated recurrent units (GRUs) or long short-term memory (LSTM) cells, which excel at capturing path-dependent phenomena. However, they suffer from long training times and time-resolution-dependent predictions that extrapolate poorly. Moreover, most existing surrogates for macro- or mesoscopic plasticity handle only relatively simple material behavior. To overcome these limitations, we introduce the Temperature-Aware Recurrent Neural Operator (TRNO), a time-resolution-independent neural architecture. We apply the TRNO to model the temperature-dependent plastic response of polycrystalline magnesium, which shows strong plastic anisotropy and thermal sensitivity. The TRNO achieves high predictive accuracy and generalizes effectively across diverse loading cases, temperatures, and time resolutions. It also outperforms conventional GRU and LSTM models in training efficiency and predictive performance. Finally, we demonstrate multiscale simulations with the TRNO, yielding a speedup of at least three orders of magnitude over traditional constitutive models.
A Learning-based Domain Decomposition Method
Jul 23, 2025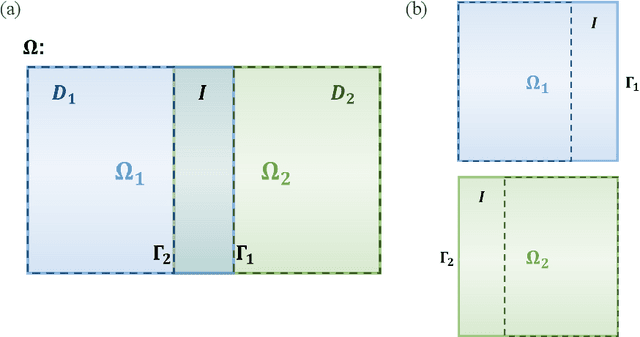
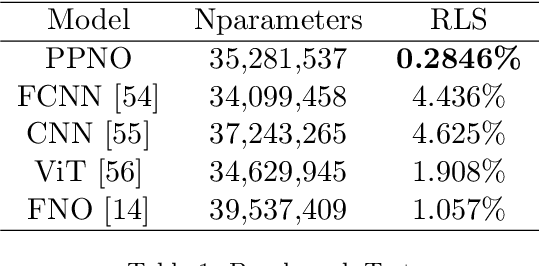
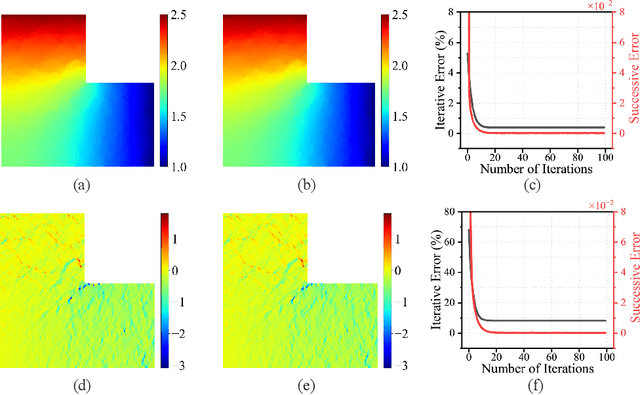
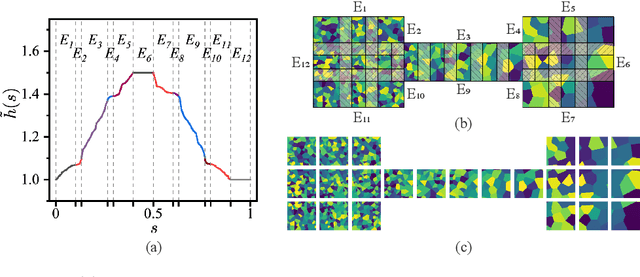
Abstract:Recent developments in mechanical, aerospace, and structural engineering have driven a growing need for efficient ways to model and analyse structures at much larger and more complex scales than before. While established numerical methods like the Finite Element Method remain reliable, they often struggle with computational cost and scalability when dealing with large and geometrically intricate problems. In recent years, neural network-based methods have shown promise because of their ability to efficiently approximate nonlinear mappings. However, most existing neural approaches are still largely limited to simple domains, which makes it difficult to apply to real-world PDEs involving complex geometries. In this paper, we propose a learning-based domain decomposition method (L-DDM) that addresses this gap. Our approach uses a single, pre-trained neural operator-originally trained on simple domains-as a surrogate model within a domain decomposition scheme, allowing us to tackle large and complicated domains efficiently. We provide a general theoretical result on the existence of neural operator approximations in the context of domain decomposition solution of abstract PDEs. We then demonstrate our method by accurately approximating solutions to elliptic PDEs with discontinuous microstructures in complex geometries, using a physics-pretrained neural operator (PPNO). Our results show that this approach not only outperforms current state-of-the-art methods on these challenging problems, but also offers resolution-invariance and strong generalization to microstructural patterns unseen during training.
A Learning-Based Optimal Uncertainty Quantification Method and Its Application to Ballistic Impact Problems
Dec 28, 2022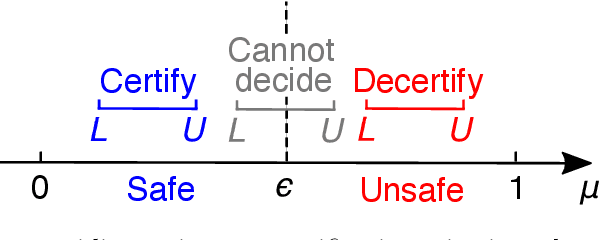
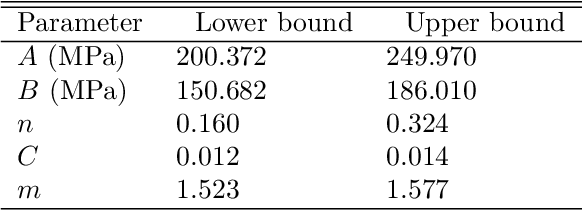
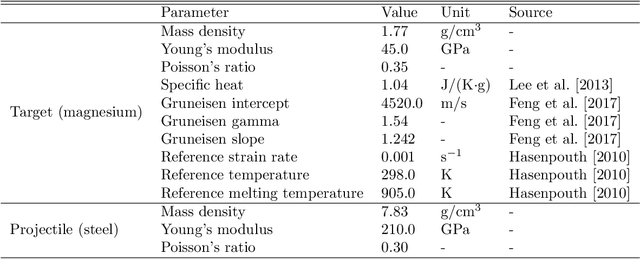
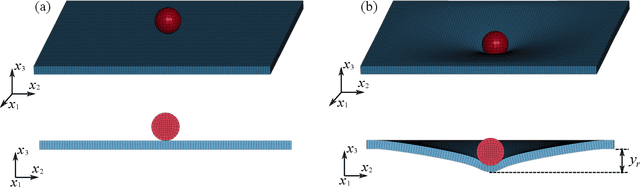
Abstract:This paper concerns the study of optimal (supremum and infimum) uncertainty bounds for systems where the input (or prior) probability measure is only partially/imperfectly known (e.g., with only statistical moments and/or on a coarse topology) rather than fully specified. Such partial knowledge provides constraints on the input probability measures. The theory of Optimal Uncertainty Quantification allows us to convert the task into a constraint optimization problem where one seeks to compute the least upper/greatest lower bound of the system's output uncertainties by finding the extremal probability measure of the input. Such optimization requires repeated evaluation of the system's performance indicator (input to performance map) and is high-dimensional and non-convex by nature. Therefore, it is difficult to find the optimal uncertainty bounds in practice. In this paper, we examine the use of machine learning, especially deep neural networks, to address the challenge. We achieve this by introducing a neural network classifier to approximate the performance indicator combined with the stochastic gradient descent method to solve the optimization problem. We demonstrate the learning based framework on the uncertainty quantification of the impact of magnesium alloys, which are promising light-weight structural and protective materials. Finally, we show that the approach can be used to construct maps for the performance certificate and safety design in engineering practice.
Fourier Neural Operator with Learned Deformations for PDEs on General Geometries
Jul 11, 2022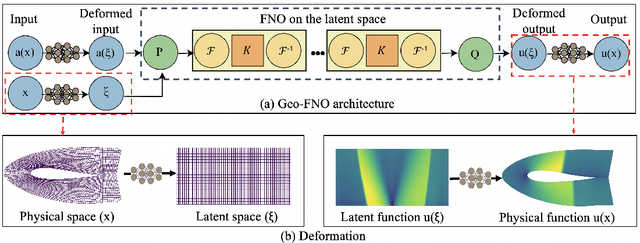
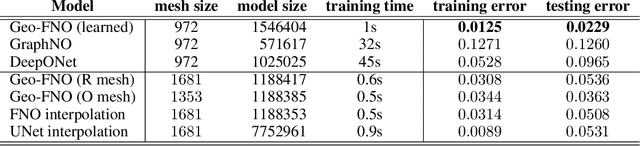
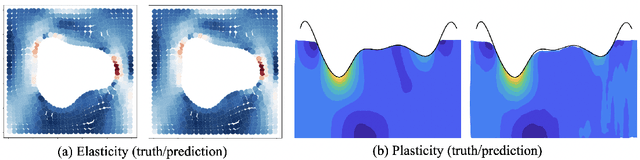
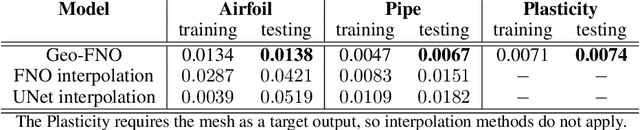
Abstract:Deep learning surrogate models have shown promise in solving partial differential equations (PDEs). Among them, the Fourier neural operator (FNO) achieves good accuracy, and is significantly faster compared to numerical solvers, on a variety of PDEs, such as fluid flows. However, the FNO uses the Fast Fourier transform (FFT), which is limited to rectangular domains with uniform grids. In this work, we propose a new framework, viz., geo-FNO, to solve PDEs on arbitrary geometries. Geo-FNO learns to deform the input (physical) domain, which may be irregular, into a latent space with a uniform grid. The FNO model with the FFT is applied in the latent space. The resulting geo-FNO model has both the computation efficiency of FFT and the flexibility of handling arbitrary geometries. Our geo-FNO is also flexible in terms of its input formats, viz., point clouds, meshes, and design parameters are all valid inputs. We consider a variety of PDEs such as the Elasticity, Plasticity, Euler's, and Navier-Stokes equations, and both forward modeling and inverse design problems. Geo-FNO is $10^5$ times faster than the standard numerical solvers and twice more accurate compared to direct interpolation on existing ML-based PDE solvers such as the standard FNO.
Physics-Informed Neural Operator for Learning Partial Differential Equations
Nov 06, 2021
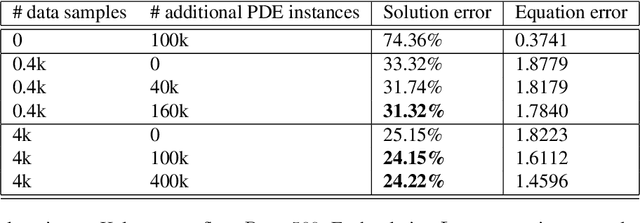
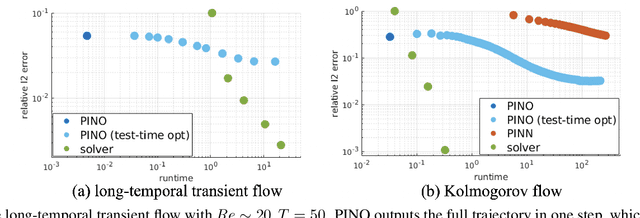

Abstract:Machine learning methods have recently shown promise in solving partial differential equations (PDEs). They can be classified into two broad categories: approximating the solution function and learning the solution operator. The Physics-Informed Neural Network (PINN) is an example of the former while the Fourier neural operator (FNO) is an example of the latter. Both these approaches have shortcomings. The optimization in PINN is challenging and prone to failure, especially on multi-scale dynamic systems. FNO does not suffer from this optimization issue since it carries out supervised learning on a given dataset, but obtaining such data may be too expensive or infeasible. In this work, we propose the physics-informed neural operator (PINO), where we combine the operating-learning and function-optimization frameworks. This integrated approach improves convergence rates and accuracy over both PINN and FNO models. In the operator-learning phase, PINO learns the solution operator over multiple instances of the parametric PDE family. In the test-time optimization phase, PINO optimizes the pre-trained operator ansatz for the querying instance of the PDE. Experiments show PINO outperforms previous ML methods on many popular PDE families while retaining the extraordinary speed-up of FNO compared to solvers. In particular, PINO accurately solves challenging long temporal transient flows and Kolmogorov flows where other baseline ML methods fail to converge.
Neural Operator: Learning Maps Between Function Spaces
Sep 06, 2021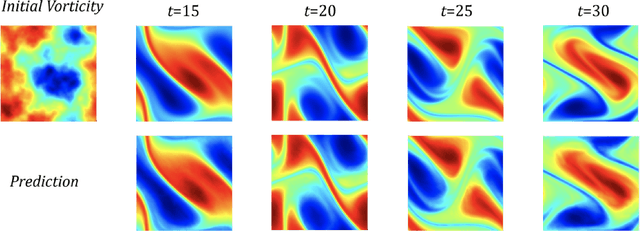
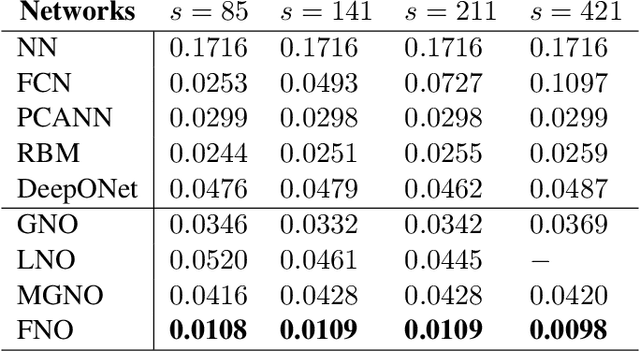
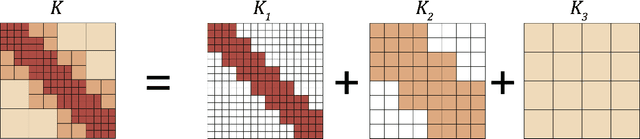
Abstract:The classical development of neural networks has primarily focused on learning mappings between finite dimensional Euclidean spaces or finite sets. We propose a generalization of neural networks tailored to learn operators mapping between infinite dimensional function spaces. We formulate the approximation of operators by composition of a class of linear integral operators and nonlinear activation functions, so that the composed operator can approximate complex nonlinear operators. We prove a universal approximation theorem for our construction. Furthermore, we introduce four classes of operator parameterizations: graph-based operators, low-rank operators, multipole graph-based operators, and Fourier operators and describe efficient algorithms for computing with each one. The proposed neural operators are resolution-invariant: they share the same network parameters between different discretizations of the underlying function spaces and can be used for zero-shot super-resolutions. Numerically, the proposed models show superior performance compared to existing machine learning based methodologies on Burgers' equation, Darcy flow, and the Navier-Stokes equation, while being several order of magnitude faster compared to conventional PDE solvers.
Markov Neural Operators for Learning Chaotic Systems
Jun 13, 2021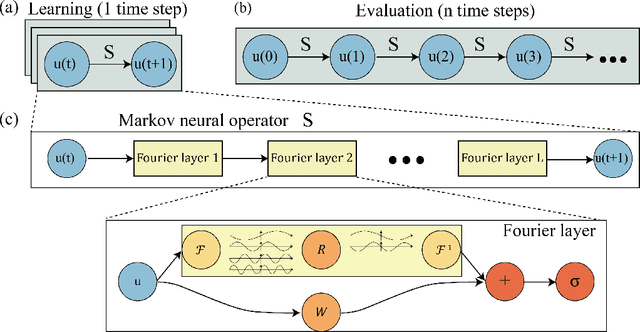
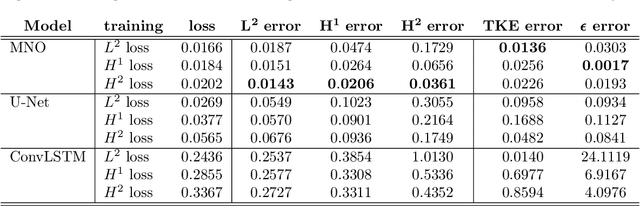
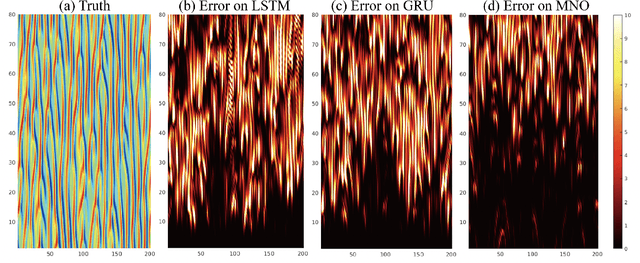
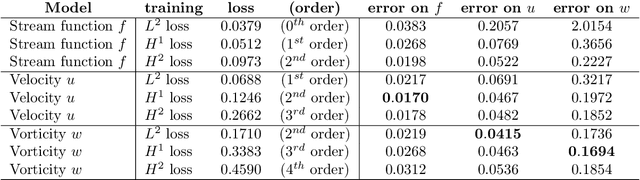
Abstract:Chaotic systems are notoriously challenging to predict because of their instability. Small errors accumulate in the simulation of each time step, resulting in completely different trajectories. However, the trajectories of many prominent chaotic systems live in a low-dimensional subspace (attractor). If the system is Markovian, the attractor is uniquely determined by the Markov operator that maps the evolution of infinitesimal time steps. This makes it possible to predict the behavior of the chaotic system by learning the Markov operator even if we cannot predict the exact trajectory. Recently, a new framework for learning resolution-invariant solution operators for PDEs was proposed, known as neural operators. In this work, we train a Markov neural operator (MNO) with only the local one-step evolution information. We then compose the learned operator to obtain the global attractor and invariant measure. Such a Markov neural operator forms a discrete semigroup and we empirically observe that does not collapse or blow up. Experiments show neural operators are more accurate and stable compared to previous methods on chaotic systems such as the Kuramoto-Sivashinsky and Navier-Stokes equations.
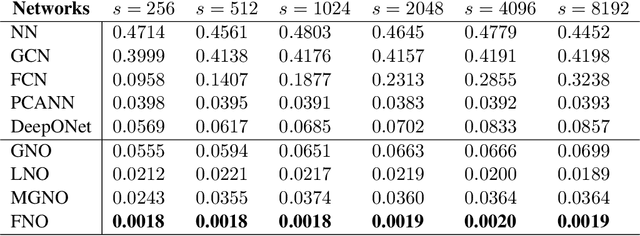
Fourier Neural Operator for Parametric Partial Differential Equations
Oct 18, 2020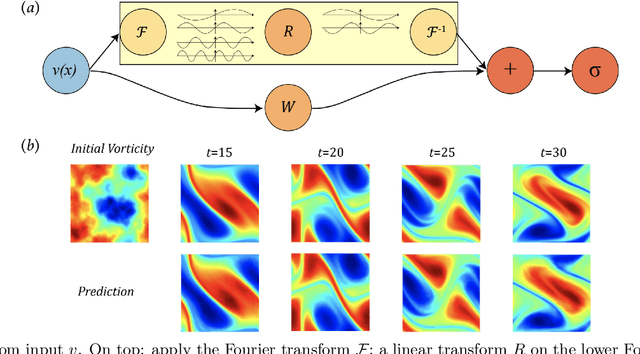
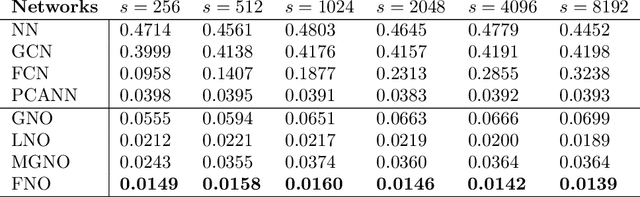
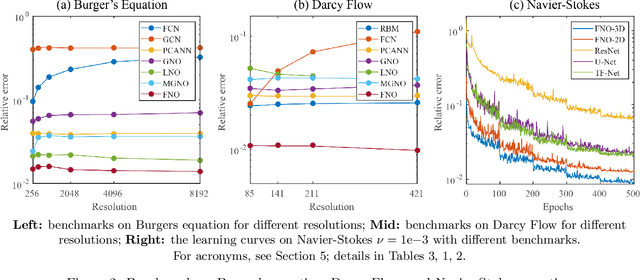
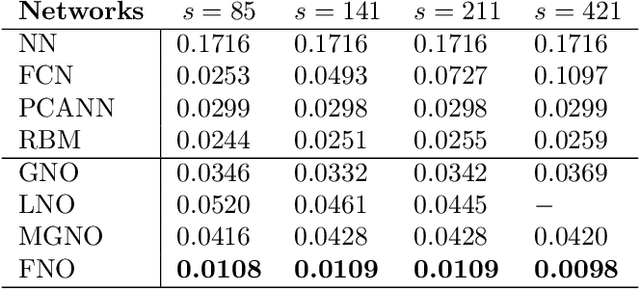
Abstract:The classical development of neural networks has primarily focused on learning mappings between finite-dimensional Euclidean spaces. Recently, this has been generalized to neural operators that learn mappings between function spaces. For partial differential equations (PDEs), neural operators directly learn the mapping from any functional parametric dependence to the solution. Thus, they learn an entire family of PDEs, in contrast to classical methods which solve one instance of the equation. In this work, we formulate a new neural operator by parameterizing the integral kernel directly in Fourier space, allowing for an expressive and efficient architecture. We perform experiments on Burgers' equation, Darcy flow, and the Navier-Stokes equation (including the turbulent regime). Our Fourier neural operator shows state-of-the-art performance compared to existing neural network methodologies and it is up to three orders of magnitude faster compared to traditional PDE solvers.
Multipole Graph Neural Operator for Parametric Partial Differential Equations
Jun 16, 2020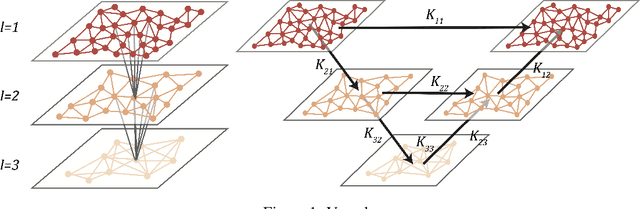
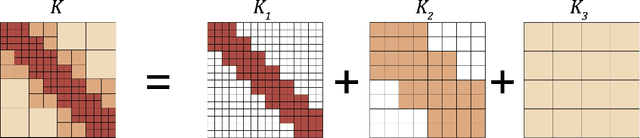
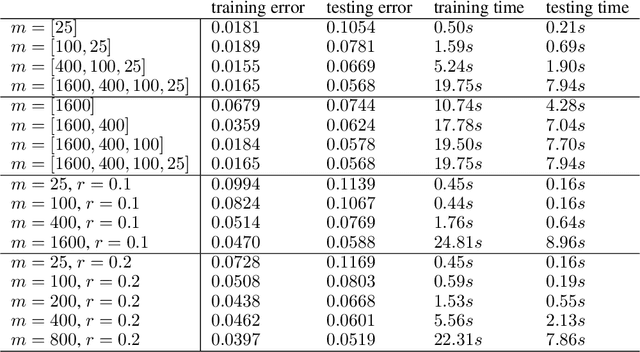
Abstract:One of the main challenges in using deep learning-based methods for simulating physical systems and solving partial differential equations (PDEs) is formulating physics-based data in the desired structure for neural networks. Graph neural networks (GNNs) have gained popularity in this area since graphs offer a natural way of modeling particle interactions and provide a clear way of discretizing the continuum models. However, the graphs constructed for approximating such tasks usually ignore long-range interactions due to unfavorable scaling of the computational complexity with respect to the number of nodes. The errors due to these approximations scale with the discretization of the system, thereby not allowing for generalization under mesh-refinement. Inspired by the classical multipole methods, we propose a novel multi-level graph neural network framework that captures interaction at all ranges with only linear complexity. Our multi-level formulation is equivalent to recursively adding inducing points to the kernel matrix, unifying GNNs with multi-resolution matrix factorization of the kernel. Experiments confirm our multi-graph network learns discretization-invariant solution operators to PDEs and can be evaluated in linear time.
Neural Operator: Graph Kernel Network for Partial Differential Equations
Mar 07, 2020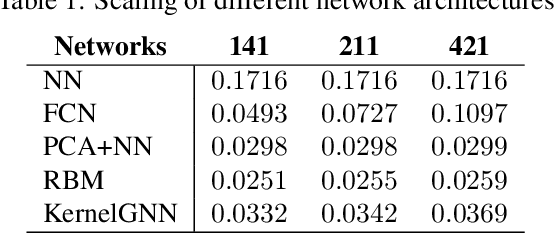
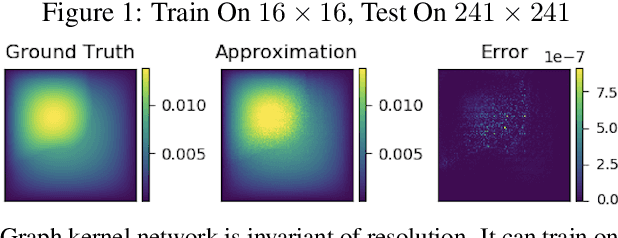

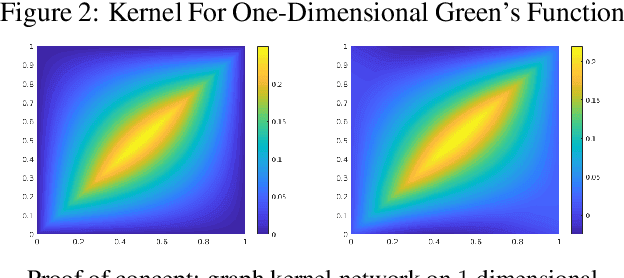
Abstract:The classical development of neural networks has been primarily for mappings between a finite-dimensional Euclidean space and a set of classes, or between two finite-dimensional Euclidean spaces. The purpose of this work is to generalize neural networks so that they can learn mappings between infinite-dimensional spaces (operators). The key innovation in our work is that a single set of network parameters, within a carefully designed network architecture, may be used to describe mappings between infinite-dimensional spaces and between different finite-dimensional approximations of those spaces. We formulate approximation of the infinite-dimensional mapping by composing nonlinear activation functions and a class of integral operators. The kernel integration is computed by message passing on graph networks. This approach has substantial practical consequences which we will illustrate in the context of mappings between input data to partial differential equations (PDEs) and their solutions. In this context, such learned networks can generalize among different approximation methods for the PDE (such as finite difference or finite element methods) and among approximations corresponding to different underlying levels of resolution and discretization. Experiments confirm that the proposed graph kernel network does have the desired properties and show competitive performance compared to the state of the art solvers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge