Multipole Graph Neural Operator for Parametric Partial Differential Equations
Paper and Code
Jun 16, 2020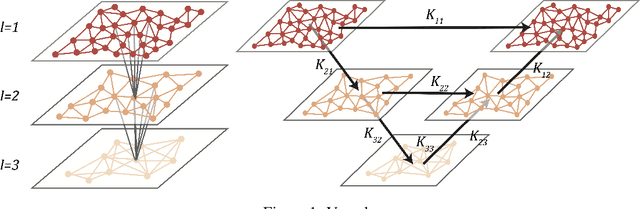
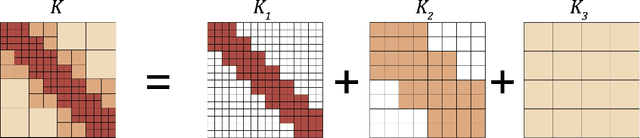
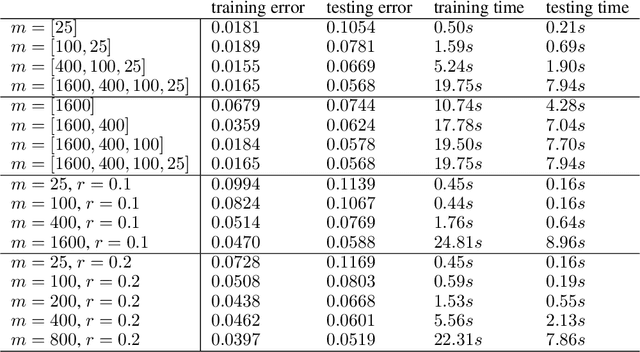
One of the main challenges in using deep learning-based methods for simulating physical systems and solving partial differential equations (PDEs) is formulating physics-based data in the desired structure for neural networks. Graph neural networks (GNNs) have gained popularity in this area since graphs offer a natural way of modeling particle interactions and provide a clear way of discretizing the continuum models. However, the graphs constructed for approximating such tasks usually ignore long-range interactions due to unfavorable scaling of the computational complexity with respect to the number of nodes. The errors due to these approximations scale with the discretization of the system, thereby not allowing for generalization under mesh-refinement. Inspired by the classical multipole methods, we propose a novel multi-level graph neural network framework that captures interaction at all ranges with only linear complexity. Our multi-level formulation is equivalent to recursively adding inducing points to the kernel matrix, unifying GNNs with multi-resolution matrix factorization of the kernel. Experiments confirm our multi-graph network learns discretization-invariant solution operators to PDEs and can be evaluated in linear time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge