Neural Operator: Graph Kernel Network for Partial Differential Equations
Paper and Code
Mar 07, 2020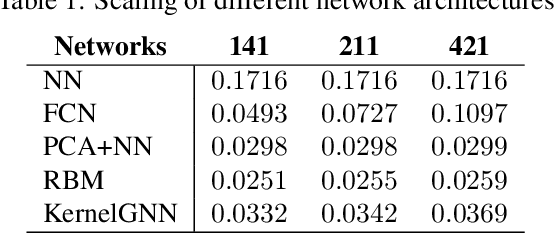
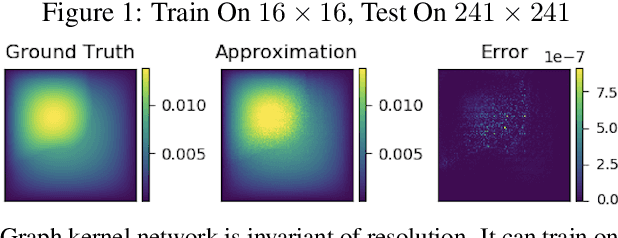

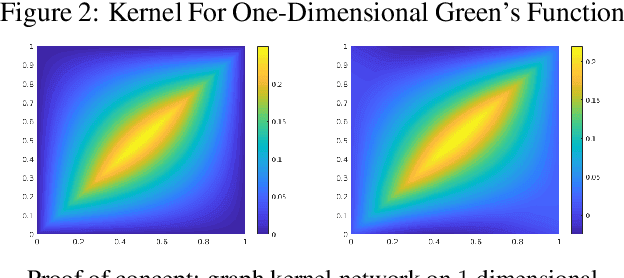
The classical development of neural networks has been primarily for mappings between a finite-dimensional Euclidean space and a set of classes, or between two finite-dimensional Euclidean spaces. The purpose of this work is to generalize neural networks so that they can learn mappings between infinite-dimensional spaces (operators). The key innovation in our work is that a single set of network parameters, within a carefully designed network architecture, may be used to describe mappings between infinite-dimensional spaces and between different finite-dimensional approximations of those spaces. We formulate approximation of the infinite-dimensional mapping by composing nonlinear activation functions and a class of integral operators. The kernel integration is computed by message passing on graph networks. This approach has substantial practical consequences which we will illustrate in the context of mappings between input data to partial differential equations (PDEs) and their solutions. In this context, such learned networks can generalize among different approximation methods for the PDE (such as finite difference or finite element methods) and among approximations corresponding to different underlying levels of resolution and discretization. Experiments confirm that the proposed graph kernel network does have the desired properties and show competitive performance compared to the state of the art solvers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge