Tensorizing flows: a tool for variational inference

Fueled by the expressive power of deep neural networks, normalizing flows have achieved spectacular success in generative modeling, or learning to draw new samples from a distribution given a finite dataset of training samples. Normalizing flows have also been applied successfully to variational inference, wherein one attempts to learn a sampler based on an expression for the log-likelihood or energy function of the distribution, rather than on data. In variational inference, the unimodality of the reference Gaussian distribution used within the normalizing flow can cause difficulties in learning multimodal distributions. We introduce an extension of normalizing flows in which the Gaussian reference is replaced with a reference distribution that is constructed via a tensor network, specifically a matrix product state or tensor train. We show that by combining flows with tensor networks on difficult variational inference tasks, we can improve on the results obtained by using either tool without the other.

High-dimensional density estimation with tensorizing flow

We propose the tensorizing flow method for estimating high-dimensional probability density functions from the observed data. The method is based on tensor-train and flow-based generative modeling. Our method first efficiently constructs an approximate density in the tensor-train form via solving the tensor cores from a linear system based on the kernel density estimators of low-dimensional marginals. We then train a continuous-time flow model from this tensor-train density to the observed empirical distribution by performing a maximum likelihood estimation. The proposed method combines the optimization-less feature of the tensor-train with the flexibility of the flow-based generative models. Numerical results are included to demonstrate the performance of the proposed method.

Autonomous learning of nonlocal stochastic neuron dynamics

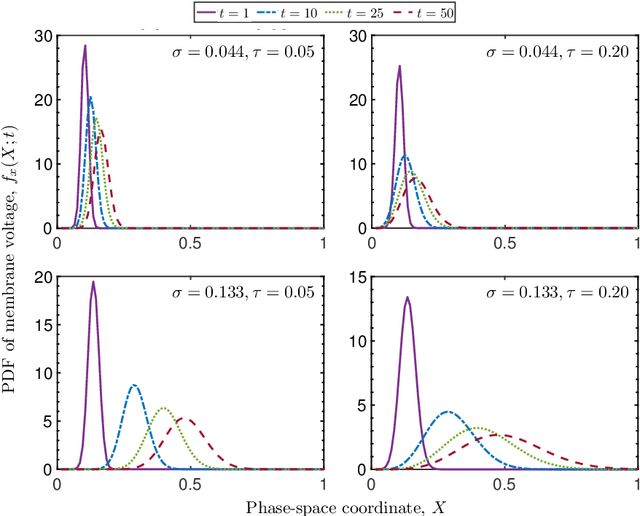
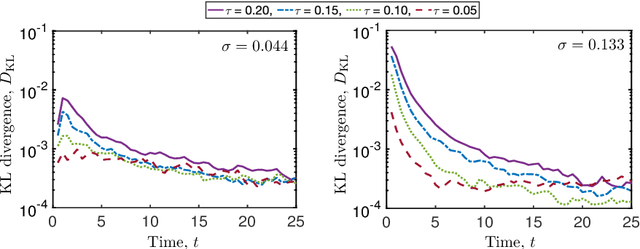
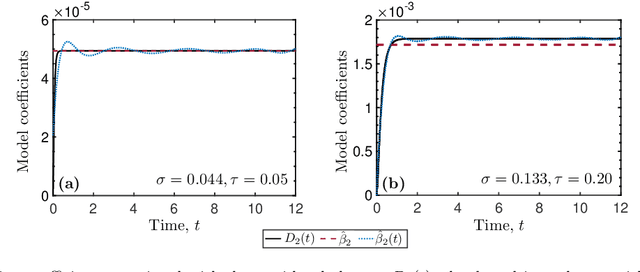
Neuronal dynamics is driven by externally imposed or internally generated random excitations/noise, and is often described by systems of stochastic ordinary differential equations. A solution to these equations is the joint probability density function (PDF) of neuron states. It can be used to calculate such information-theoretic quantities as the mutual information between the stochastic stimulus and various internal states of the neuron (e.g., membrane potential), as well as various spiking statistics. When random excitations are modeled as Gaussian white noise, the joint PDF of neuron states satisfies exactly a Fokker-Planck equation. However, most biologically plausible noise sources are correlated (colored). In this case, the resulting PDF equations require a closure approximation. We propose two methods for closing such equations: a modified nonlocal large-eddy-diffusivity closure and a data-driven closure relying on sparse regression to learn relevant features. The closures are tested for stochastic leaky integrate-and-fire (LIF) and FitzHugh-Nagumo (FHN) neurons driven by sine-Wiener noise. Mutual information and total correlation between the random stimulus and the internal states of the neuron are calculated for the FHN neuron.