Transfer Learning on Multi-Dimensional Data: A Novel Approach to Neural Network-Based Surrogate Modeling

The development of efficient surrogates of partial differential equations (PDEs) is a critical step towards scalable modeling of complex, multiscale systems-of-systems. Convolutional neural networks (CNNs) have gained popularity as the basis for such surrogate models due to their success in capturing high-dimensional input-output mappings and the negligible cost of a forward pass. However, the high cost of generating training data -- typically via classical numerical solvers -- raises the question of whether these models are worth pursuing over more straightforward alternatives with well-established theoretical foundations, such as Monte Carlo methods. To reduce the cost of data generation, we propose training a CNN surrogate model on a mixture of numerical solutions to both the $d$-dimensional problem and its ($d-1$)-dimensional approximation, taking advantage of the efficiency savings guaranteed by the curse of dimensionality. We demonstrate our approach on a multiphase flow test problem, using transfer learning to train a dense fully-convolutional encoder-decoder CNN on the two classes of data. Numerical results from a sample uncertainty quantification task demonstrate that our surrogate model outperforms Monte Carlo with several times the data generation budget.

Baseflow identification via explainable AI with Kolmogorov-Arnold networks

Hydrological models often involve constitutive laws that may not be optimal in every application. We propose to replace such laws with the Kolmogorov-Arnold networks (KANs), a class of neural networks designed to identify symbolic expressions. We demonstrate KAN's potential on the problem of baseflow identification, a notoriously challenging task plagued by significant uncertainty. KAN-derived functional dependencies of the baseflow components on the aridity index outperform their original counterparts. On a test set, they increase the Nash-Sutcliffe Efficiency (NSE) by 67%, decrease the root mean squared error by 30%, and increase the Kling-Gupta efficiency by 24%. This superior performance is achieved while reducing the number of fitting parameters from three to two. Next, we use data from 378 catchments across the continental United States to refine the water-balance equation at the mean-annual scale. The KAN-derived equations based on the refined water balance outperform both the current aridity index model, with up to a 105% increase in NSE, and the KAN-derived equations based on the original water balance. While the performance of our model and tree-based machine learning methods is similar, KANs offer the advantage of simplicity and transparency and require no specific software or computational tools. This case study focuses on the aridity index formulation, but the approach is flexible and transferable to other hydrological processes.

High-Precision Geosteering via Reinforcement Learning and Particle Filters

Geosteering, a key component of drilling operations, traditionally involves manual interpretation of various data sources such as well-log data. This introduces subjective biases and inconsistent procedures. Academic attempts to solve geosteering decision optimization with greedy optimization and Approximate Dynamic Programming (ADP) showed promise but lacked adaptivity to realistic diverse scenarios. Reinforcement learning (RL) offers a solution to these challenges, facilitating optimal decision-making through reward-based iterative learning. State estimation methods, e.g., particle filter (PF), provide a complementary strategy for geosteering decision-making based on online information. We integrate an RL-based geosteering with PF to address realistic geosteering scenarios. Our framework deploys PF to process real-time well-log data to estimate the location of the well relative to the stratigraphic layers, which then informs the RL-based decision-making process. We compare our method's performance with that of using solely either RL or PF. Our findings indicate a synergy between RL and PF in yielding optimized geosteering decisions.

Neural oscillators for magnetic hysteresis modeling

Hysteresis is a ubiquitous phenomenon in science and engineering; its modeling and identification are crucial for understanding and optimizing the behavior of various systems. We develop an ordinary differential equation-based recurrent neural network (RNN) approach to model and quantify the hysteresis, which manifests itself in sequentiality and history-dependence. Our neural oscillator, HystRNN, draws inspiration from coupled-oscillatory RNN and phenomenological hysteresis models to update the hidden states. The performance of HystRNN is evaluated to predict generalized scenarios, involving first-order reversal curves and minor loops. The findings show the ability of HystRNN to generalize its behavior to previously untrained regions, an essential feature that hysteresis models must have. This research highlights the advantage of neural oscillators over the traditional RNN-based methods in capturing complex hysteresis patterns in magnetic materials, where traditional rate-dependent methods are inadequate to capture intrinsic nonlinearity.

Neural oscillators for generalization of physics-informed machine learning

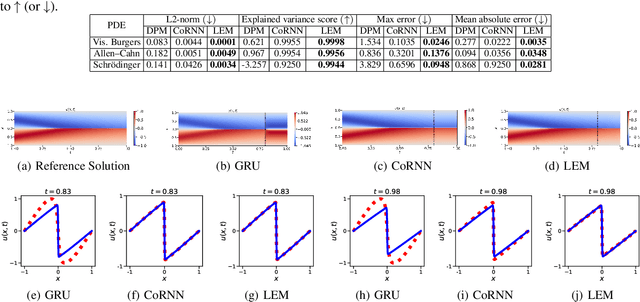
A primary challenge of physics-informed machine learning (PIML) is its generalization beyond the training domain, especially when dealing with complex physical problems represented by partial differential equations (PDEs). This paper aims to enhance the generalization capabilities of PIML, facilitating practical, real-world applications where accurate predictions in unexplored regions are crucial. We leverage the inherent causality and temporal sequential characteristics of PDE solutions to fuse PIML models with recurrent neural architectures based on systems of ordinary differential equations, referred to as neural oscillators. Through effectively capturing long-time dependencies and mitigating the exploding and vanishing gradient problem, neural oscillators foster improved generalization in PIML tasks. Extensive experimentation involving time-dependent nonlinear PDEs and biharmonic beam equations demonstrates the efficacy of the proposed approach. Incorporating neural oscillators outperforms existing state-of-the-art methods on benchmark problems across various metrics. Consequently, the proposed method improves the generalization capabilities of PIML, providing accurate solutions for extrapolation and prediction beyond the training data.

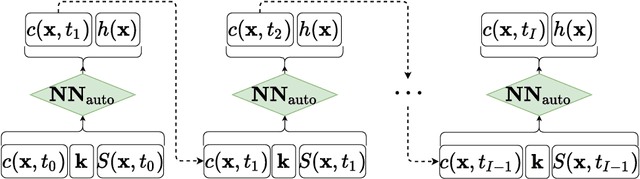
Learning Nonautonomous Systems via Dynamic Mode Decomposition

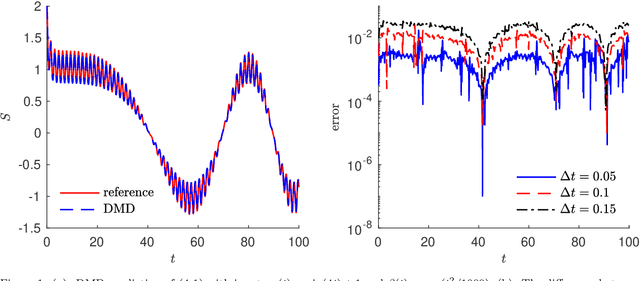
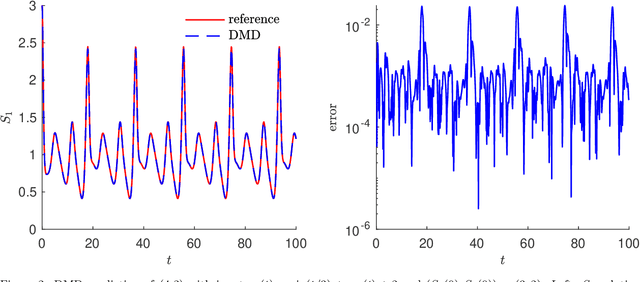
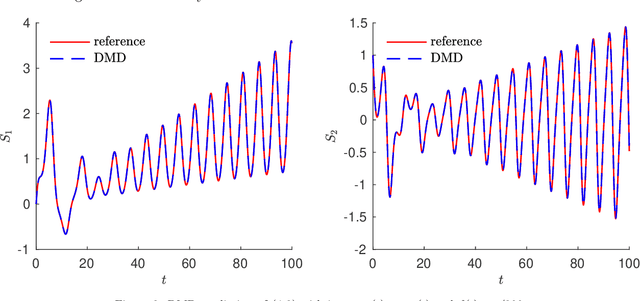
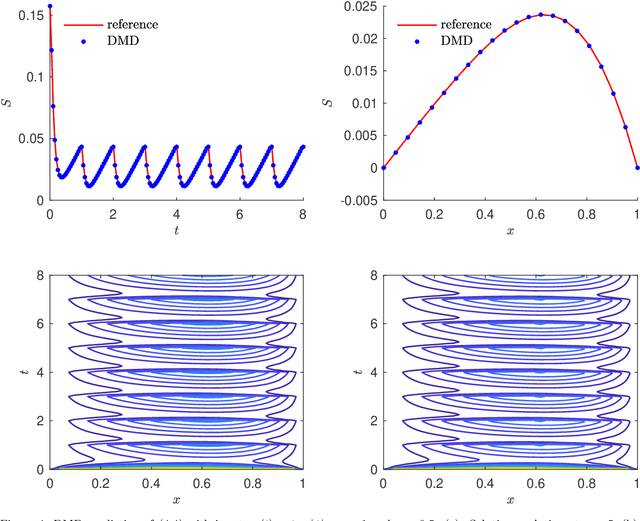
We present a data-driven learning approach for unknown nonautonomous dynamical systems with time-dependent inputs based on dynamic mode decomposition (DMD). To circumvent the difficulty of approximating the time-dependent Koopman operators for nonautonomous systems, a modified system derived from local parameterization of the external time-dependent inputs is employed as an approximation to the original nonautonomous system. The modified system comprises a sequence of local parametric systems, which can be well approximated by a parametric surrogate model using our previously proposed framework for dimension reduction and interpolation in parameter space (DRIPS). The offline step of DRIPS relies on DMD to build a linear surrogate model, endowed with reduced-order bases (ROBs), for the observables mapped from training data. Then the offline step constructs a sequence of iterative parametric surrogate models from interpolations on suitable manifolds, where the target/test parameter points are specified by the local parameterization of the test external time-dependent inputs. We present a number of numerical examples to demonstrate the robustness of our method and compare its performance with deep neural networks in the same settings.

Discovering Sparse Hysteresis Models: A Data-driven Study for Piezoelectric Materials and Perspectives on Magnetic Hysteresis

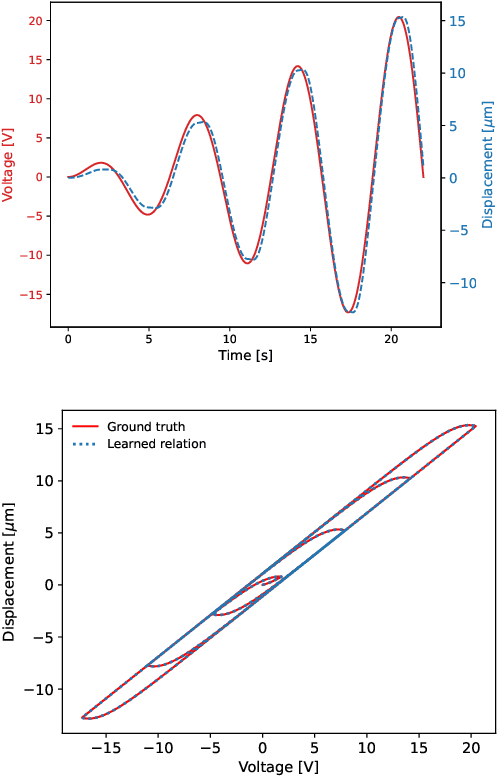
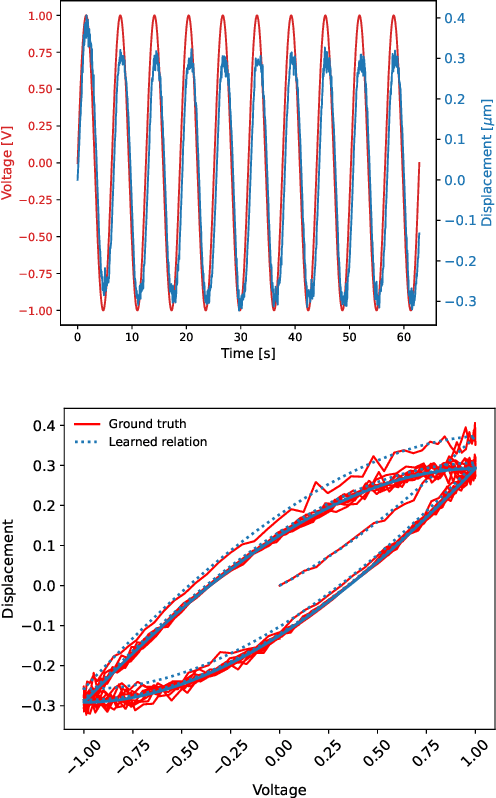
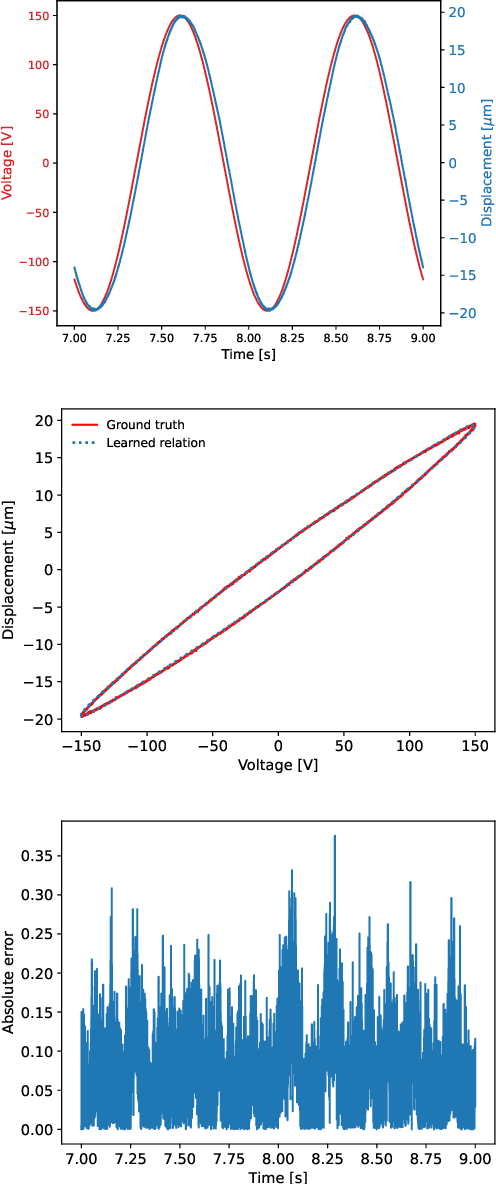
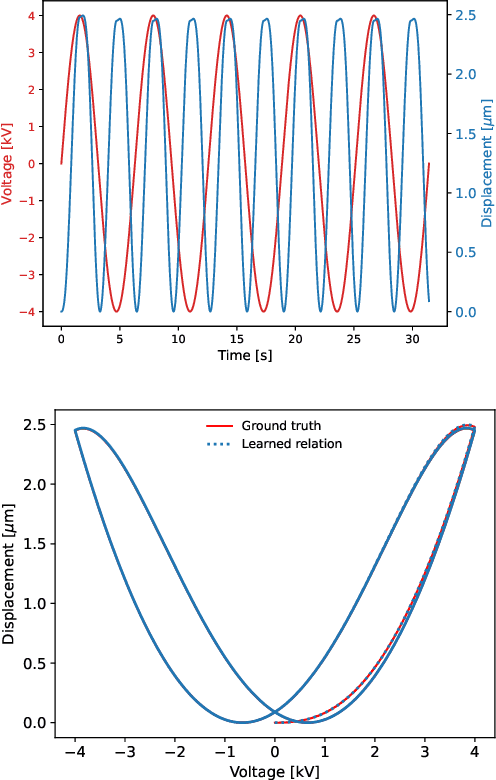
This article presents an approach for modelling hysteresis in piezoelectric materials that leverages recent advancements in machine learning, particularly in sparse-regression techniques. While sparse regression has previously been used to model various scientific and engineering phenomena, its application to nonlinear hysteresis modelling in piezoelectric materials has yet to be explored. The study employs the least-squares algorithm with sequential threshold to model the dynamic system responsible for hysteresis, resulting in a concise model that accurately predicts hysteresis for both simulated and experimental piezoelectric material data. Additionally, insights are provided on sparse white-box modelling of hysteresis for magnetic materials taking non-oriented electrical steel as an example. The presented approach is compared to traditional regression-based and neural network methods, demonstrating its efficiency and robustness.

Machine Learning in Heterogeneous Porous Materials

The "Workshop on Machine learning in heterogeneous porous materials" brought together international scientific communities of applied mathematics, porous media, and material sciences with experts in the areas of heterogeneous materials, machine learning (ML) and applied mathematics to identify how ML can advance materials research. Within the scope of ML and materials research, the goal of the workshop was to discuss the state-of-the-art in each community, promote crosstalk and accelerate multi-disciplinary collaborative research, and identify challenges and opportunities. As the end result, four topic areas were identified: ML in predicting materials properties, and discovery and design of novel materials, ML in porous and fractured media and time-dependent phenomena, Multi-scale modeling in heterogeneous porous materials via ML, and Discovery of materials constitutive laws and new governing equations. This workshop was part of the AmeriMech Symposium series sponsored by the National Academies of Sciences, Engineering and Medicine and the U.S. National Committee on Theoretical and Applied Mechanics.

Deep Learning for Simultaneous Inference of Hydraulic and Transport Properties

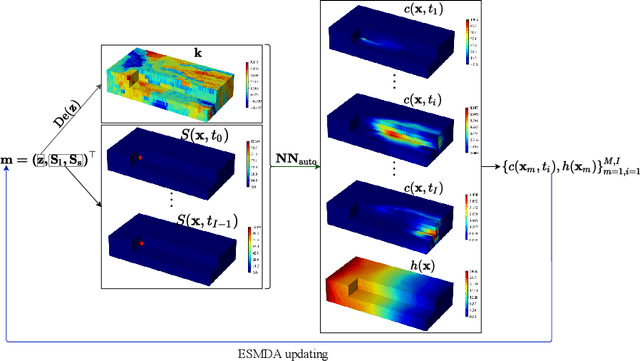
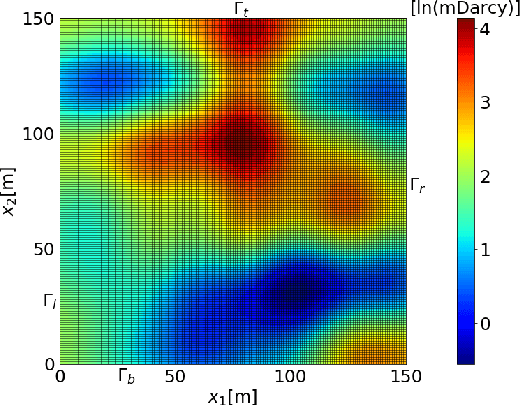
Identifying the heterogeneous conductivity field and reconstructing the contaminant release history are key aspects of subsurface remediation. Achieving these two goals with limited and noisy hydraulic head and concentration measurements is challenging. The obstacles include solving an inverse problem for high-dimensional parameters, and the high-computational cost needed for the repeated forward modeling. We use a convolutional adversarial autoencoder (CAAE) for the parameterization of the heterogeneous non-Gaussian conductivity field with a low-dimensional latent representation. Additionally, we trained a three-dimensional dense convolutional encoder-decoder (DenseED) network to serve as the forward surrogate for the flow and transport processes. Combining the CAAE and DenseED forward surrogate models, the ensemble smoother with multiple data assimilation (ESMDA) algorithm is used to sample from the Bayesian posterior distribution of the unknown parameters, forming a CAAE-DenseED-ESMDA inversion framework. We applied this CAAE-DenseED-ESMDA inversion framework in a three-dimensional contaminant source and conductivity field identification problem. A comparison of the inversion results from CAAE-ESMDA with physical flow and transport simulator and CAAE-DenseED-ESMDA is provided, showing that accurate reconstruction results were achieved with a much higher computational efficiency.

Transfer Learning on Multi-Fidelity Data

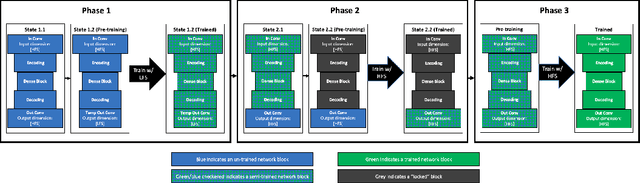
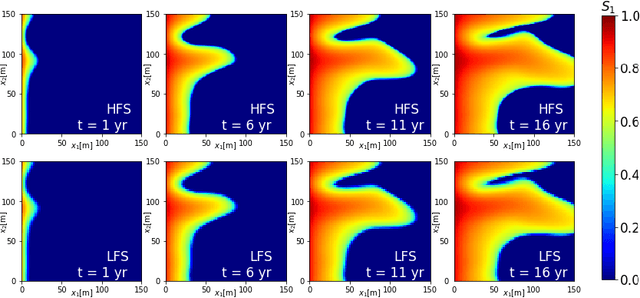
Neural networks (NNs) are often used as surrogates or emulators of partial differential equations (PDEs) that describe the dynamics of complex systems. A virtually negligible computational cost of such surrogates renders them an attractive tool for ensemble-based computation, which requires a large number of repeated PDE solves. Since the latter are also needed to generate sufficient data for NN training, the usefulness of NN-based surrogates hinges on the balance between the training cost and the computational gain stemming from their deployment. We rely on multi-fidelity simulations to reduce the cost of data generation for subsequent training of a deep convolutional NN (CNN) using transfer learning. High- and low-fidelity images are generated by solving PDEs on fine and coarse meshes, respectively. We use theoretical results for multilevel Monte Carlo to guide our choice of the numbers of images of each kind. We demonstrate the performance of this multi-fidelity training strategy on the problem of estimation of the distribution of a quantity of interest, whose dynamics is governed by a system of nonlinear PDEs (parabolic PDEs of multi-phase flow in heterogeneous porous media) with uncertain/random parameters. Our numerical experiments demonstrate that a mixture of a comparatively large number of low-fidelity data and smaller numbers of high- and low-fidelity data provides an optimal balance of computational speed-up and prediction accuracy. The former is reported relative to both CNN training on high-fidelity images only and Monte Carlo solution of the PDEs. The latter is expressed in terms of both the Wasserstein distance and the Kullback-Leibler divergence.