Abhishek Chandra
Neuro-Symbolic Operator for Interpretable and Generalizable Characterization of Complex Piezoelectric Systems
May 30, 2025



Abstract:Complex piezoelectric systems are foundational in industrial applications. Their performance, however, is challenged by the nonlinear voltage-displacement hysteretic relationships. Efficient characterization methods are, therefore, essential for reliable design, monitoring, and maintenance. Recently proposed neural operator methods serve as surrogates for system characterization but face two pressing issues: interpretability and generalizability. State-of-the-art (SOTA) neural operators are black-boxes, providing little insight into the learned operator. Additionally, generalizing them to novel voltages and predicting displacement profiles beyond the training domain is challenging, limiting their practical use. To address these limitations, this paper proposes a neuro-symbolic operator (NSO) framework that derives the analytical operators governing hysteretic relationships. NSO first learns a Fourier neural operator mapping voltage fields to displacement profiles, followed by a library-based sparse model discovery method, generating white-box parsimonious models governing the underlying hysteresis. These models enable accurate and interpretable prediction of displacement profiles across varying and out-of-distribution voltage fields, facilitating generalizability. The potential of NSO is demonstrated by accurately predicting voltage-displacement hysteresis, including butterfly-shaped relationships. Moreover, NSO predicts displacement profiles even for noisy and low-fidelity voltage data, emphasizing its robustness. The results highlight the advantages of NSO compared to SOTA neural operators and model discovery methods on several evaluation metrics. Consequently, NSO contributes to characterizing complex piezoelectric systems while improving the interpretability and generalizability of neural operators, essential for design, monitoring, maintenance, and other real-world scenarios.
Beyond Accuracy: EcoL2 Metric for Sustainable Neural PDE Solvers
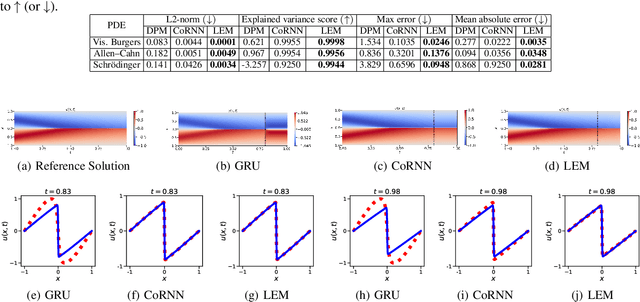
May 18, 2025Abstract:Real-world systems, from aerospace to railway engineering, are modeled with partial differential equations (PDEs) describing the physics of the system. Estimating robust solutions for such problems is essential. Deep learning-based architectures, such as neural PDE solvers, have recently gained traction as a reliable solution method. The current state of development of these approaches, however, primarily focuses on improving accuracy. The environmental impact of excessive computation, leading to increased carbon emissions, has largely been overlooked. This paper introduces a carbon emission measure for a range of PDE solvers. Our proposed metric, EcoL2, balances model accuracy with emissions across data collection, model training, and deployment. Experiments across both physics-informed machine learning and operator learning architectures demonstrate that the proposed metric presents a holistic assessment of model performance and emission cost. As such solvers grow in scale and deployment, EcoL2 represents a step toward building performant scientific machine learning systems with lower long-term environmental impact.
Magnetic Hysteresis Modeling with Neural Operators
Jul 03, 2024



Abstract:Hysteresis modeling is crucial to comprehend the behavior of magnetic devices, facilitating optimal designs. Hitherto, deep learning-based methods employed to model hysteresis, face challenges in generalizing to novel input magnetic fields. This paper addresses the generalization challenge by proposing neural operators for modeling constitutive laws that exhibit magnetic hysteresis by learning a mapping between magnetic fields. In particular, two prominent neural operators -- deep operator network and Fourier neural operator -- are employed to predict novel first-order reversal curves and minor loops, where novel means they are not used to train the model. In addition, a rate-independent Fourier neural operator is proposed to predict material responses at sampling rates different from those used during training to incorporate the rate-independent characteristics of magnetic hysteresis. The presented numerical experiments demonstrate that neural operators efficiently model magnetic hysteresis, outperforming the traditional neural recurrent methods on various metrics and generalizing to novel magnetic fields. The findings emphasize the advantages of using neural operators for modeling hysteresis under varying magnetic conditions, underscoring their importance in characterizing magnetic material based devices.
A Biased Estimator for MinMax Sampling and Distributed Aggregation
Apr 26, 2024



Abstract:MinMax sampling is a technique for downsampling a real-valued vector which minimizes the maximum variance over all vector components. This approach is useful for reducing the amount of data that must be sent over a constrained network link (e.g. in the wide-area). MinMax can provide unbiased estimates of the vector elements, along with unbiased estimates of aggregates when vectors are combined from multiple locations. In this work, we propose a biased MinMax estimation scheme, B-MinMax, which trades an increase in estimator bias for a reduction in variance. We prove that when no aggregation is performed, B-MinMax obtains a strictly lower MSE compared to the unbiased MinMax estimator. When aggregation is required, B-MinMax is preferable when sample sizes are small or the number of aggregated vectors is limited. Our experiments show that this approach can substantially reduce the MSE for MinMax sampling in many practical settings.
Neural oscillators for magnetic hysteresis modeling
Aug 23, 2023



Abstract:Hysteresis is a ubiquitous phenomenon in science and engineering; its modeling and identification are crucial for understanding and optimizing the behavior of various systems. We develop an ordinary differential equation-based recurrent neural network (RNN) approach to model and quantify the hysteresis, which manifests itself in sequentiality and history-dependence. Our neural oscillator, HystRNN, draws inspiration from coupled-oscillatory RNN and phenomenological hysteresis models to update the hidden states. The performance of HystRNN is evaluated to predict generalized scenarios, involving first-order reversal curves and minor loops. The findings show the ability of HystRNN to generalize its behavior to previously untrained regions, an essential feature that hysteresis models must have. This research highlights the advantage of neural oscillators over the traditional RNN-based methods in capturing complex hysteresis patterns in magnetic materials, where traditional rate-dependent methods are inadequate to capture intrinsic nonlinearity.
Neural oscillators for generalization of physics-informed machine learning
Aug 17, 2023


Abstract:A primary challenge of physics-informed machine learning (PIML) is its generalization beyond the training domain, especially when dealing with complex physical problems represented by partial differential equations (PDEs). This paper aims to enhance the generalization capabilities of PIML, facilitating practical, real-world applications where accurate predictions in unexplored regions are crucial. We leverage the inherent causality and temporal sequential characteristics of PDE solutions to fuse PIML models with recurrent neural architectures based on systems of ordinary differential equations, referred to as neural oscillators. Through effectively capturing long-time dependencies and mitigating the exploding and vanishing gradient problem, neural oscillators foster improved generalization in PIML tasks. Extensive experimentation involving time-dependent nonlinear PDEs and biharmonic beam equations demonstrates the efficacy of the proposed approach. Incorporating neural oscillators outperforms existing state-of-the-art methods on benchmark problems across various metrics. Consequently, the proposed method improves the generalization capabilities of PIML, providing accurate solutions for extrapolation and prediction beyond the training data.
Discovering Sparse Hysteresis Models: A Data-driven Study for Piezoelectric Materials and Perspectives on Magnetic Hysteresis
Feb 16, 2023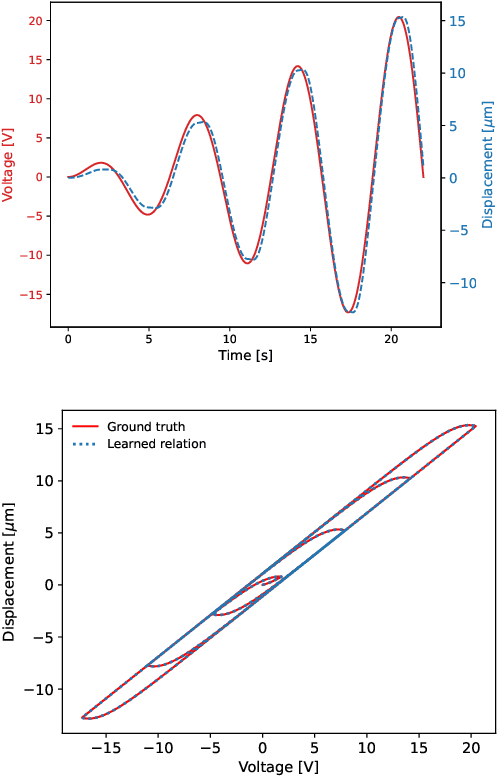
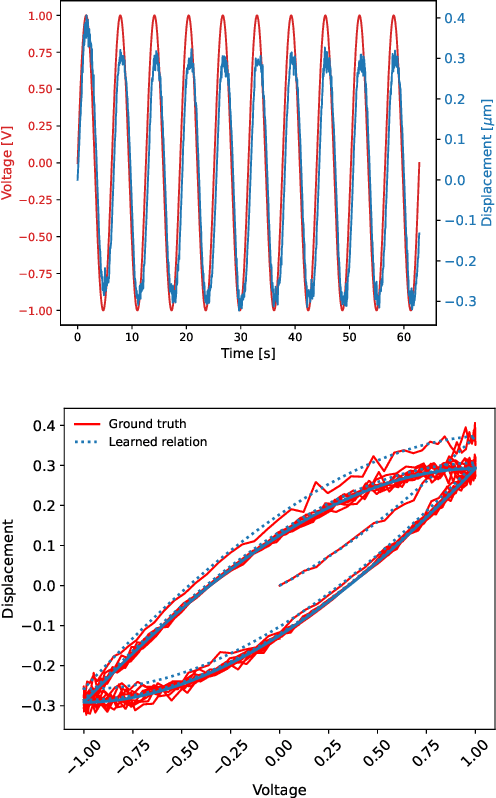
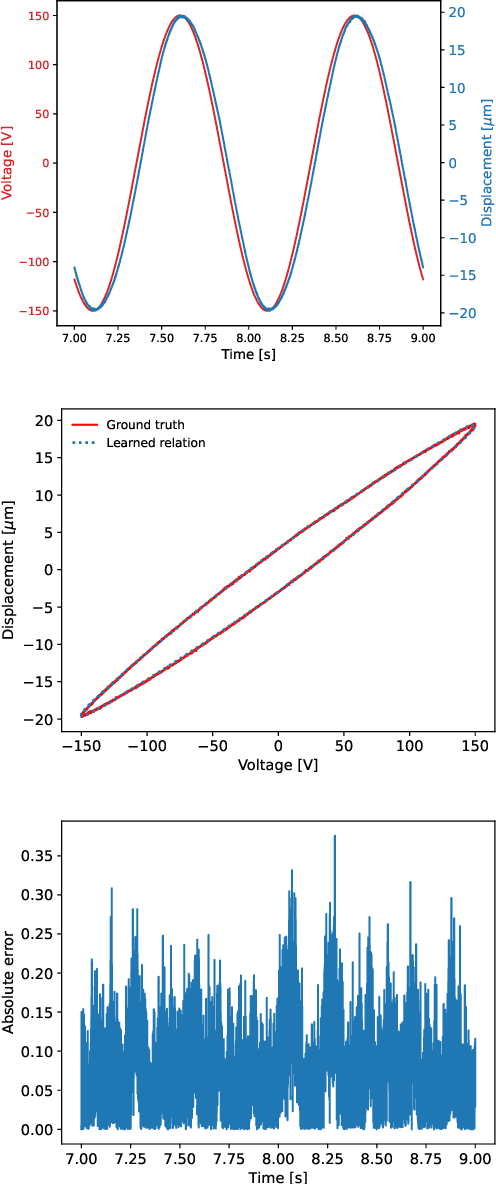
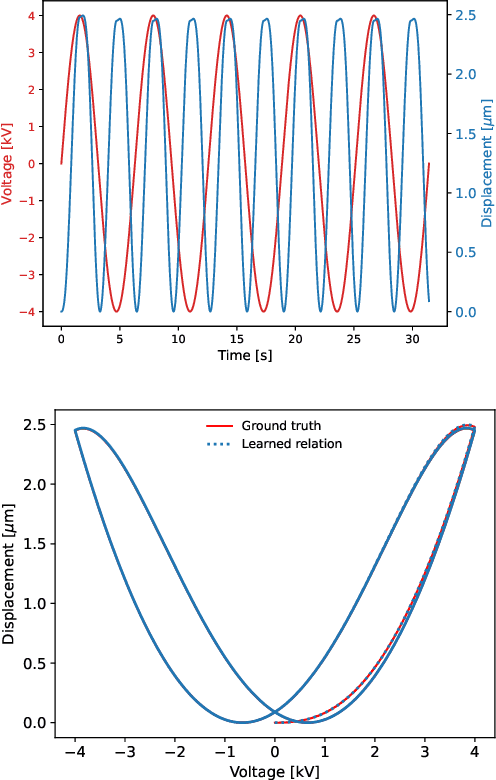
Abstract:This article presents an approach for modelling hysteresis in piezoelectric materials that leverages recent advancements in machine learning, particularly in sparse-regression techniques. While sparse regression has previously been used to model various scientific and engineering phenomena, its application to nonlinear hysteresis modelling in piezoelectric materials has yet to be explored. The study employs the least-squares algorithm with sequential threshold to model the dynamic system responsible for hysteresis, resulting in a concise model that accurately predicts hysteresis for both simulated and experimental piezoelectric material data. Additionally, insights are provided on sparse white-box modelling of hysteresis for magnetic materials taking non-oriented electrical steel as an example. The presented approach is compared to traditional regression-based and neural network methods, demonstrating its efficiency and robustness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge