Magnetic Hysteresis Modeling with Neural Operators

Hysteresis modeling is crucial to comprehend the behavior of magnetic devices, facilitating optimal designs. Hitherto, deep learning-based methods employed to model hysteresis, face challenges in generalizing to novel input magnetic fields. This paper addresses the generalization challenge by proposing neural operators for modeling constitutive laws that exhibit magnetic hysteresis by learning a mapping between magnetic fields. In particular, two prominent neural operators -- deep operator network and Fourier neural operator -- are employed to predict novel first-order reversal curves and minor loops, where novel means they are not used to train the model. In addition, a rate-independent Fourier neural operator is proposed to predict material responses at sampling rates different from those used during training to incorporate the rate-independent characteristics of magnetic hysteresis. The presented numerical experiments demonstrate that neural operators efficiently model magnetic hysteresis, outperforming the traditional neural recurrent methods on various metrics and generalizing to novel magnetic fields. The findings emphasize the advantages of using neural operators for modeling hysteresis under varying magnetic conditions, underscoring their importance in characterizing magnetic material based devices.

A computationally lightweight safe learning algorithm

Safety is an essential asset when learning control policies for physical systems, as violating safety constraints during training can lead to expensive hardware damage. In response to this need, the field of safe learning has emerged with algorithms that can provide probabilistic safety guarantees without knowledge of the underlying system dynamics. Those algorithms often rely on Gaussian process inference. Unfortunately, Gaussian process inference scales cubically with the number of data points, limiting applicability to high-dimensional and embedded systems. In this paper, we propose a safe learning algorithm that provides probabilistic safety guarantees but leverages the Nadaraya-Watson estimator instead of Gaussian processes. For the Nadaraya-Watson estimator, we can reach logarithmic scaling with the number of data points. We provide theoretical guarantees for the estimates, embed them into a safe learning algorithm, and show numerical experiments on a simulated seven-degrees-of-freedom robot manipulator.

Neural oscillators for magnetic hysteresis modeling

Hysteresis is a ubiquitous phenomenon in science and engineering; its modeling and identification are crucial for understanding and optimizing the behavior of various systems. We develop an ordinary differential equation-based recurrent neural network (RNN) approach to model and quantify the hysteresis, which manifests itself in sequentiality and history-dependence. Our neural oscillator, HystRNN, draws inspiration from coupled-oscillatory RNN and phenomenological hysteresis models to update the hidden states. The performance of HystRNN is evaluated to predict generalized scenarios, involving first-order reversal curves and minor loops. The findings show the ability of HystRNN to generalize its behavior to previously untrained regions, an essential feature that hysteresis models must have. This research highlights the advantage of neural oscillators over the traditional RNN-based methods in capturing complex hysteresis patterns in magnetic materials, where traditional rate-dependent methods are inadequate to capture intrinsic nonlinearity.

Discovering Sparse Hysteresis Models: A Data-driven Study for Piezoelectric Materials and Perspectives on Magnetic Hysteresis

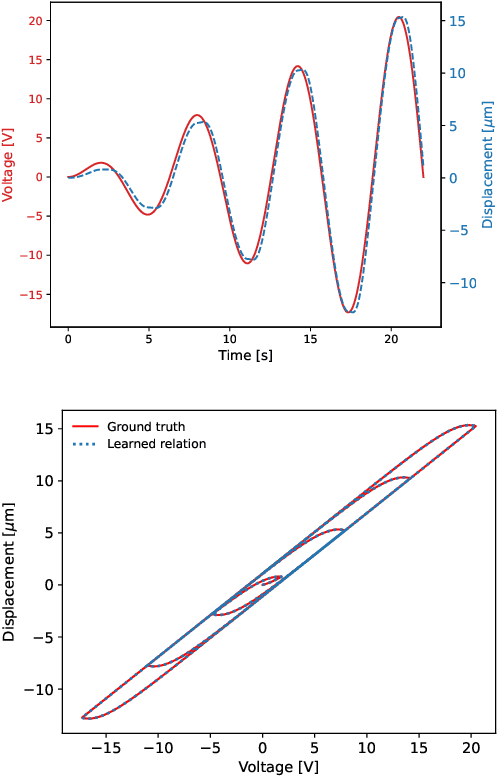
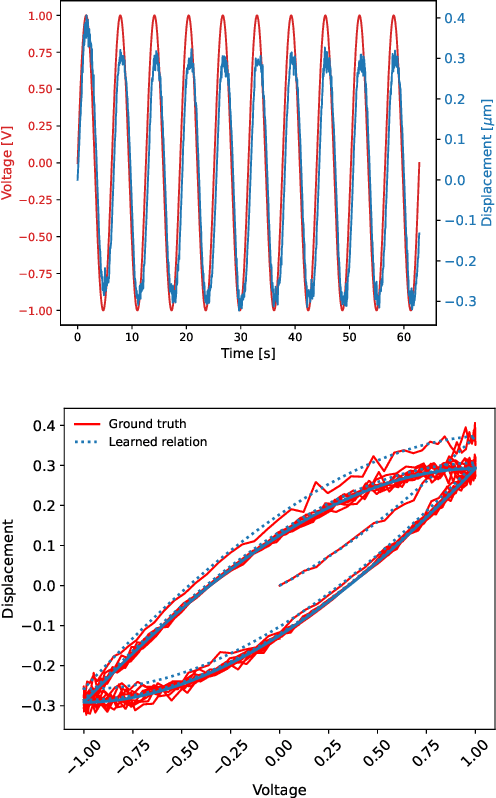
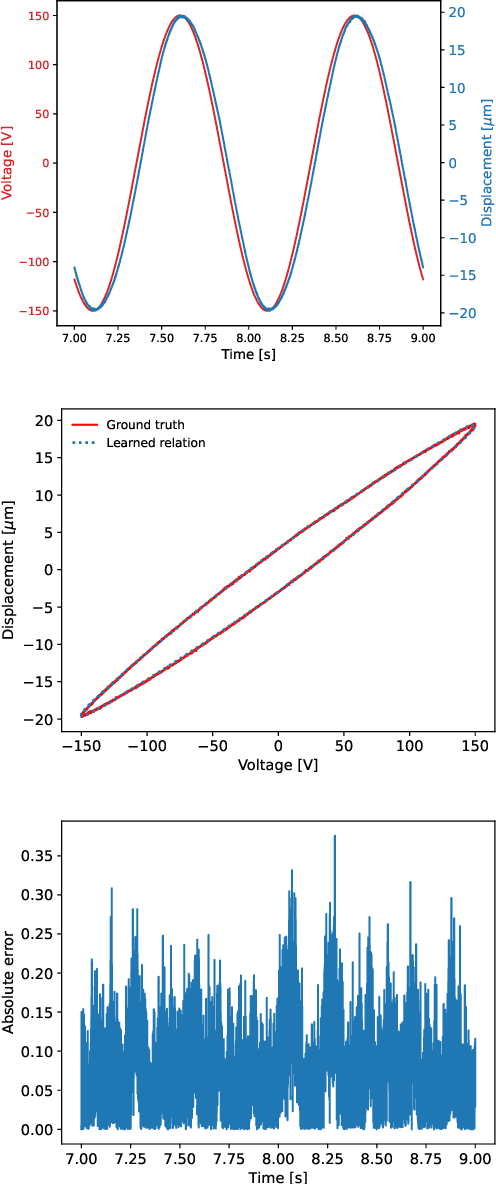
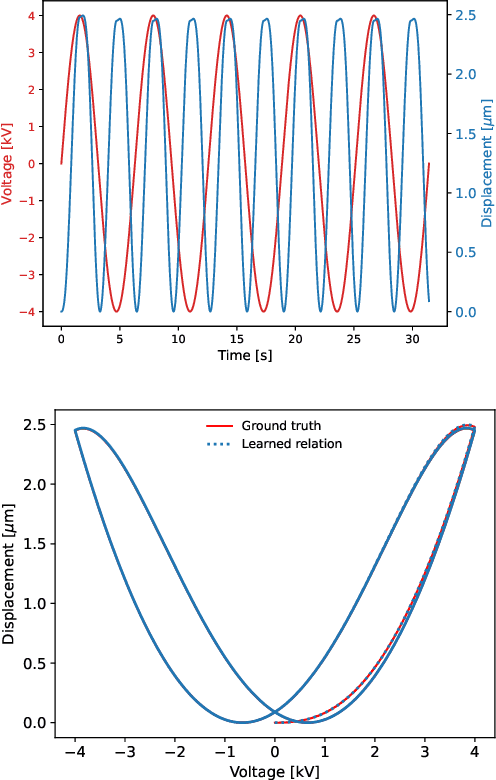
This article presents an approach for modelling hysteresis in piezoelectric materials that leverages recent advancements in machine learning, particularly in sparse-regression techniques. While sparse regression has previously been used to model various scientific and engineering phenomena, its application to nonlinear hysteresis modelling in piezoelectric materials has yet to be explored. The study employs the least-squares algorithm with sequential threshold to model the dynamic system responsible for hysteresis, resulting in a concise model that accurately predicts hysteresis for both simulated and experimental piezoelectric material data. Additionally, insights are provided on sparse white-box modelling of hysteresis for magnetic materials taking non-oriented electrical steel as an example. The presented approach is compared to traditional regression-based and neural network methods, demonstrating its efficiency and robustness.

Decoupling multivariate functions using a nonparametric filtered tensor decomposition

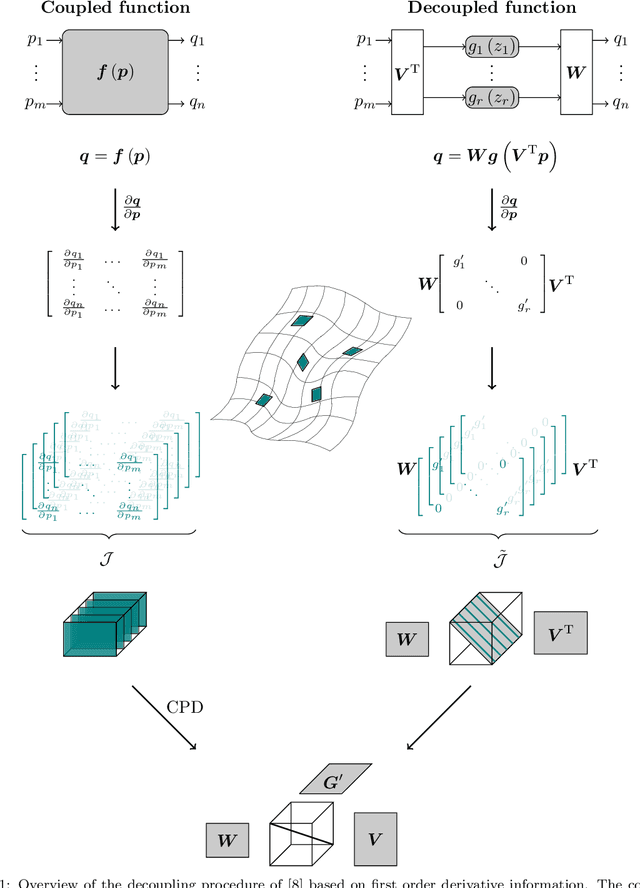
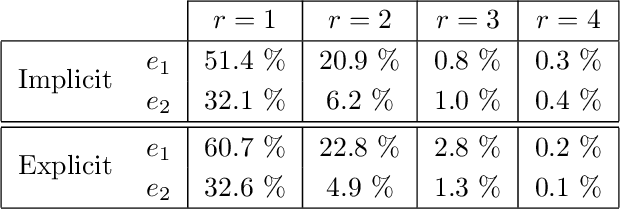
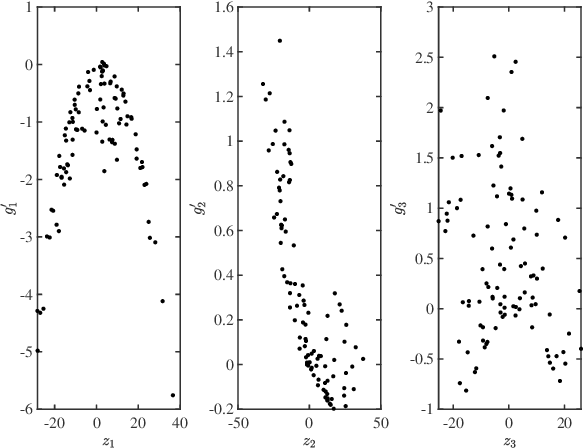
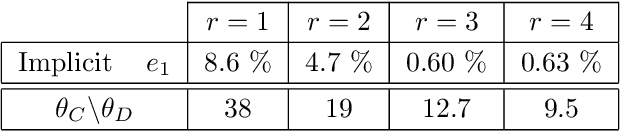
Multivariate functions emerge naturally in a wide variety of data-driven models. Popular choices are expressions in the form of basis expansions or neural networks. While highly effective, the resulting functions tend to be hard to interpret, in part because of the large number of required parameters. Decoupling techniques aim at providing an alternative representation of the nonlinearity. The so-called decoupled form is often a more efficient parameterisation of the relationship while being highly structured, favouring interpretability. In this work two new algorithms, based on filtered tensor decompositions of first order derivative information are introduced. The method returns nonparametric estimates of smooth decoupled functions. Direct applications are found in, i.a. the fields of nonlinear system identification and machine learning.

Deep Convolutional Networks in System Identification

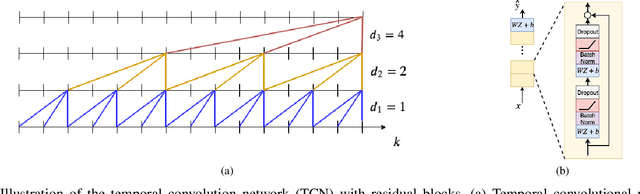
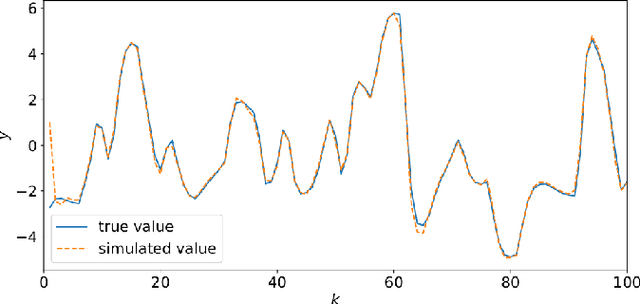
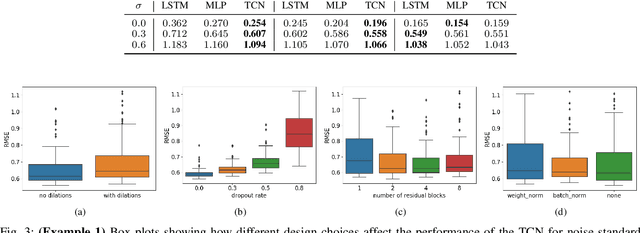
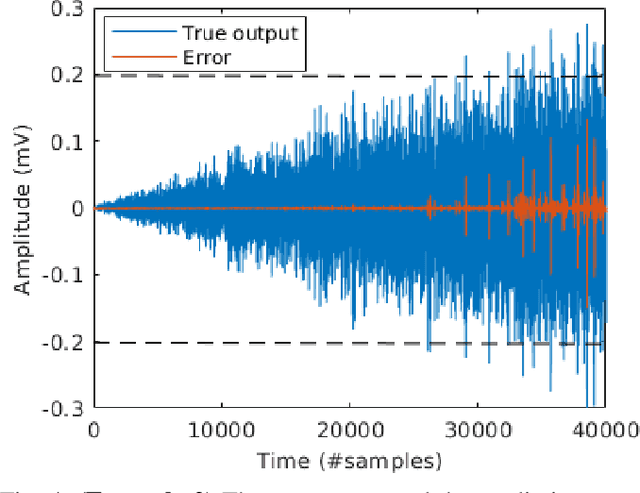
Recent developments within deep learning are relevant for nonlinear system identification problems. In this paper, we establish connections between the deep learning and the system identification communities. It has recently been shown that convolutional architectures are at least as capable as recurrent architectures when it comes to sequence modeling tasks. Inspired by these results we explore the explicit relationships between the recently proposed temporal convolutional network (TCN) and two classic system identification model structures; Volterra series and block-oriented models. We end the paper with an experimental study where we provide results on two real-world problems, the well-known Silverbox dataset and a newer dataset originating from ground vibration experiments on an F-16 fighter aircraft.

The trade-off between long-term memory and smoothness for recurrent networks

Training recurrent neural networks (RNNs) that possess long-term memory is challenging. We provide insight into the trade-off between the smoothness of the cost function and the memory retention capabilities of the network. We express both aspects in terms of the Lipschitz constant of the dynamics modeled by the network. This allows us to make a distinction between three types of regions in the parameter space. In the first region, the network experiences problems in retaining long-term information, while at the same time the cost function is smooth and easy for gradient descent to navigate in. In the second region, the amount of stored information increases with time and the cost function is intricate and full of local minima. The third region is in between the two other regions and here the RNN is able to retain long-term information. Based on these theoretical findings we present the hypothesis that good parameter choices for the RNN are located in between the well-behaved and the ill-behaved cost function regions. The concepts presented in the paper are illustrated by artificially generated and real examples.

On the Smoothness of Nonlinear System Identification

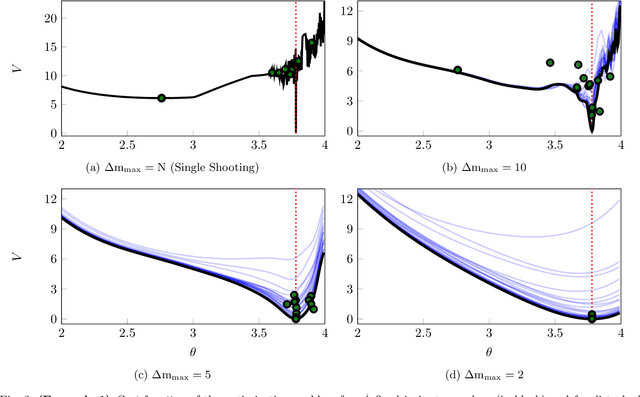
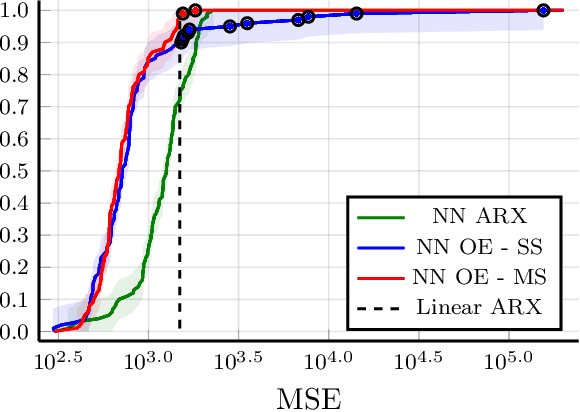
New light is shed onto optimization problems resulting from prediction error parameter estimation of linear and nonlinear systems. It is shown that the smoothness" of the objective function depends both on the simulation length and on the decay rate of the prediction model. More precisely, for regions of the parameter space where the model is not contractive, the Lipschitz constant and $\beta$-smoothness of the objective function might blow up exponentially with the simulation length, making it hard to numerically find minima within those regions or, even, to escape from them. In addition to providing theoretical understanding of this problem, this paper also proposes the use of multiple shooting as a viable solution. The proposed method minimizes the error between a prediction model and observed values. Rather than running the prediction model over the entire dataset, as in the original prediction error formulation, multiple shooting splits the data into smaller subsets and runs the prediction model over each subdivision, making the simulation length a design parameter and making it possible to solve problems that would be infeasible using a standard approach. The equivalence with the original problem is obtained by including constraints in the optimization. The method is illustrated for the parameter estimation of nonlinear systems with chaotic or unstable behavior, as well as on neural network parameter estimation.