The trade-off between long-term memory and smoothness for recurrent networks

Training recurrent neural networks (RNNs) that possess long-term memory is challenging. We provide insight into the trade-off between the smoothness of the cost function and the memory retention capabilities of the network. We express both aspects in terms of the Lipschitz constant of the dynamics modeled by the network. This allows us to make a distinction between three types of regions in the parameter space. In the first region, the network experiences problems in retaining long-term information, while at the same time the cost function is smooth and easy for gradient descent to navigate in. In the second region, the amount of stored information increases with time and the cost function is intricate and full of local minima. The third region is in between the two other regions and here the RNN is able to retain long-term information. Based on these theoretical findings we present the hypothesis that good parameter choices for the RNN are located in between the well-behaved and the ill-behaved cost function regions. The concepts presented in the paper are illustrated by artificially generated and real examples.

On the Smoothness of Nonlinear System Identification

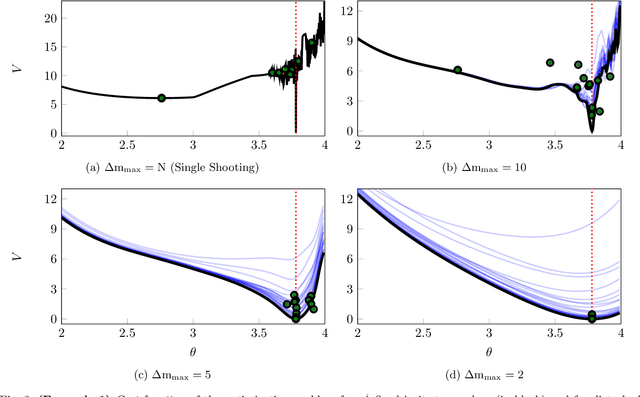
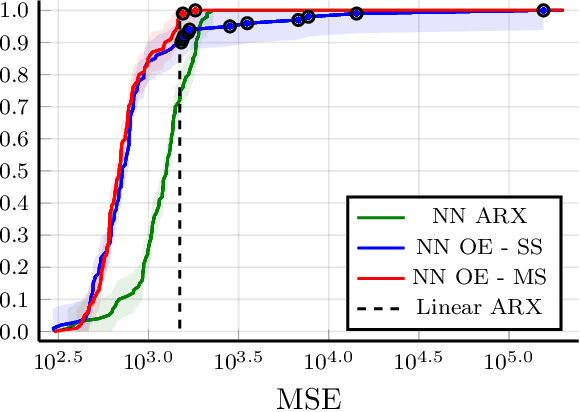
New light is shed onto optimization problems resulting from prediction error parameter estimation of linear and nonlinear systems. It is shown that the smoothness" of the objective function depends both on the simulation length and on the decay rate of the prediction model. More precisely, for regions of the parameter space where the model is not contractive, the Lipschitz constant and $\beta$-smoothness of the objective function might blow up exponentially with the simulation length, making it hard to numerically find minima within those regions or, even, to escape from them. In addition to providing theoretical understanding of this problem, this paper also proposes the use of multiple shooting as a viable solution. The proposed method minimizes the error between a prediction model and observed values. Rather than running the prediction model over the entire dataset, as in the original prediction error formulation, multiple shooting splits the data into smaller subsets and runs the prediction model over each subdivision, making the simulation length a design parameter and making it possible to solve problems that would be infeasible using a standard approach. The equivalence with the original problem is obtained by including constraints in the optimization. The method is illustrated for the parameter estimation of nonlinear systems with chaotic or unstable behavior, as well as on neural network parameter estimation.

"Parallel Training Considered Harmful?": Comparing series-parallel and parallel feedforward network training

Neural network models for dynamic systems can be trained either in parallel or in series-parallel configurations. Influenced by early arguments, several papers justify the choice of series-parallel rather than parallel configuration claiming it has a lower computational cost, better stability properties during training and provides more accurate results. Other published results, on the other hand, defend parallel training as being more robust and capable of yielding more accu- rate long-term predictions. The main contribution of this paper is to present a study comparing both methods under the same unified framework. We focus on three aspects: i) robustness of the estimation in the presence of noise; ii) computational cost; and, iii) convergence. A unifying mathematical framework and simulation studies show situations where each training method provides better validation results, being parallel training better in what is believed to be more realistic scenarios. An example using measured data seems to reinforce such claim. We also show, with a novel complexity analysis and numerical examples, that both methods have similar computational cost, being series series-parallel training, however, more amenable to parallelization. Some informal discussion about stability and convergence properties is presented and explored in the examples.

Lasso Regularization Paths for NARMAX Models via Coordinate Descent

We propose a new algorithm for estimating NARMAX models with $L_1$ regularization for models represented as a linear combination of basis functions. Due to the $L_1$-norm penalty the Lasso estimation tends to produce some coefficients that are exactly zero and hence gives interpretable models. The novelty of the contribution is the inclusion of error regressors in the Lasso estimation (which yields a nonlinear regression problem). The proposed algorithm uses cyclical coordinate descent to compute the parameters of the NARMAX models for the entire regularization path. It deals with the error terms by updating the regressor matrix along with the parameter vector. In comparative timings we find that the modification does not reduce the computational efficiency of the original algorithm and can provide the most important regressors in very few inexpensive iterations. The method is illustrated for linear and polynomial models by means of two examples.