BEAVER: Building Environments with Assessable Variation for Evaluating Multi-Objective Reinforcement Learning

Recent years have seen significant advancements in designing reinforcement learning (RL)-based agents for building energy management. While individual success is observed in simulated or controlled environments, the scalability of RL approaches in terms of efficiency and generalization across building dynamics and operational scenarios remains an open question. In this work, we formally characterize the generalization space for the cross-environment, multi-objective building energy management task, and formulate the multi-objective contextual RL problem. Such a formulation helps understand the challenges of transferring learned policies across varied operational contexts such as climate and heat convection dynamics under multiple control objectives such as comfort level and energy consumption. We provide a principled way to parameterize such contextual information in realistic building RL environments, and construct a novel benchmark to facilitate the evaluation of generalizable RL algorithms in practical building control tasks. Our results show that existing multi-objective RL methods are capable of achieving reasonable trade-offs between conflicting objectives. However, their performance degrades under certain environment variations, underscoring the importance of incorporating dynamics-dependent contextual information into the policy learning process.

Constrained Diffusers for Safe Planning and Control

Diffusion models have shown remarkable potential in planning and control tasks due to their ability to represent multimodal distributions over actions and trajectories. However, ensuring safety under constraints remains a critical challenge for diffusion models. This paper proposes Constrained Diffusers, a novel framework that incorporates constraints into pre-trained diffusion models without retraining or architectural modifications. Inspired by constrained optimization, we apply a constrained Langevin sampling mechanism for the reverse diffusion process that jointly optimizes the trajectory and realizes constraint satisfaction through three iterative algorithms: projected method, primal-dual method and augmented Lagrangian approaches. In addition, we incorporate discrete control barrier functions as constraints for constrained diffusers to guarantee safety in online implementation. Experiments in Maze2D, locomotion, and pybullet ball running tasks demonstrate that our proposed methods achieve constraint satisfaction with less computation time, and are competitive to existing methods in environments with static and time-varying constraints.

Improved Sample Complexity of Imitation Learning for Barrier Model Predictive Control

Recent work in imitation learning has shown that having an expert controller that is both suitably smooth and stable enables stronger guarantees on the performance of the learned controller. However, constructing such smoothed expert controllers for arbitrary systems remains challenging, especially in the presence of input and state constraints. As our primary contribution, we show how such a smoothed expert can be designed for a general class of systems using a log-barrier-based relaxation of a standard Model Predictive Control (MPC) optimization problem. Improving upon our previous work, we show that barrier MPC achieves theoretically optimal error-to-smoothness tradeoff along some direction. At the core of this theoretical guarantee on smoothness is an improved lower bound we prove on the optimality gap of the analytic center associated with a convex Lipschitz function, which we believe could be of independent interest. We validate our theoretical findings via experiments, demonstrating the merits of our smoothing approach over randomized smoothing.

Smooth Model Predictive Control with Applications to Statistical Learning

Statistical learning theory and high dimensional statistics have had a tremendous impact on Machine Learning theory and have impacted a variety of domains including systems and control theory. Over the past few years we have witnessed a variety of applications of such theoretical tools to help answer questions such as: how many state-action pairs are needed to learn a static control policy to a given accuracy? Recent results have shown that continuously differentiable and stabilizing control policies can be well-approximated using neural networks with hard guarantees on performance, yet often even the simplest constrained control problems are not smooth. To address this void, in this paper we study smooth approximations of linear Model Predictive Control (MPC) policies, in which hard constraints are replaced by barrier functions, a.k.a. barrier MPC. In particular, we show that barrier MPC inherits the exponential stability properties of the original non-smooth MPC policy. Using a careful analysis of the proposed barrier MPC, we show that its smoothness constant can be carefully controlled, thereby paving the way for new sample complexity results for approximating MPC policies from sampled state-action pairs.

Globally Convergent Policy Search over Dynamic Filters for Output Estimation

We introduce the first direct policy search algorithm which provably converges to the globally optimal $\textit{dynamic}$ filter for the classical problem of predicting the outputs of a linear dynamical system, given noisy, partial observations. Despite the ubiquity of partial observability in practice, theoretical guarantees for direct policy search algorithms, one of the backbones of modern reinforcement learning, have proven difficult to achieve. This is primarily due to the degeneracies which arise when optimizing over filters that maintain internal state. In this paper, we provide a new perspective on this challenging problem based on the notion of $\textit{informativity}$, which intuitively requires that all components of a filter's internal state are representative of the true state of the underlying dynamical system. We show that informativity overcomes the aforementioned degeneracy. Specifically, we propose a $\textit{regularizer}$ which explicitly enforces informativity, and establish that gradient descent on this regularized objective - combined with a ``reconditioning step'' - converges to the globally optimal cost a $\mathcal{O}(1/T)$ rate. Our analysis relies on several new results which may be of independent interest, including a new framework for analyzing non-convex gradient descent via convex reformulation, and novel bounds on the solution to linear Lyapunov equations in terms of (our quantitative measure of) informativity.

Stabilizing Dynamical Systems via Policy Gradient Methods

Stabilizing an unknown control system is one of the most fundamental problems in control systems engineering. In this paper, we provide a simple, model-free algorithm for stabilizing fully observed dynamical systems. While model-free methods have become increasingly popular in practice due to their simplicity and flexibility, stabilization via direct policy search has received surprisingly little attention. Our algorithm proceeds by solving a series of discounted LQR problems, where the discount factor is gradually increased. We prove that this method efficiently recovers a stabilizing controller for linear systems, and for smooth, nonlinear systems within a neighborhood of their equilibria. Our approach overcomes a significant limitation of prior work, namely the need for a pre-given stabilizing control policy. We empirically evaluate the effectiveness of our approach on common control benchmarks.

Distributed Identification of Contracting and/or Monotone Network Dynamics

This paper proposes methods for identification of large-scale networked systems with guarantees that the resulting model will be contracting -- a strong form of nonlinear stability -- and/or monotone, i.e. order relations between states are preserved. The main challenges that we address are: simultaneously searching for model parameters and a certificate of stability, and scalability to networks with hundreds or thousands of nodes. We propose a model set that admits convex constraints for stability and monotonicity, and has a separable structure that allows distributed identification via the alternating directions method of multipliers (ADMM). The performance and scalability of the approach is illustrated on a variety of linear and non-linear case studies, including a nonlinear traffic network with a 200-dimensional state space.

Optimistic robust linear quadratic dual control

Recent work by Mania et al. has proved that certainty equivalent control achieves nearly optimal regret for linear systems with quadratic costs. However, when parameter uncertainty is large, certainty equivalence cannot be relied upon to stabilize the true, unknown system. In this paper, we present a dual control strategy that attempts to combine the performance of certainty equivalence, with the practical utility of robustness. The formulation preserves structure in the representation of parametric uncertainty, which allows the controller to target reduction of uncertainty in the parameters that `matter most' for the control task, while robustly stabilizing the uncertain system. Control synthesis proceeds via convex optimization, and the method is illustrated on a numerical example.

Robust exploration in linear quadratic reinforcement learning

This paper concerns the problem of learning control policies for an unknown linear dynamical system to minimize a quadratic cost function. We present a method, based on convex optimization, that accomplishes this task robustly: i.e., we minimize the worst-case cost, accounting for system uncertainty given the observed data. The method balances exploitation and exploration, exciting the system in such a way so as to reduce uncertainty in the model parameters to which the worst-case cost is most sensitive. Numerical simulations and application to a hardware-in-the-loop servo-mechanism demonstrate the approach, with appreciable performance and robustness gains over alternative methods observed in both.

On the Smoothness of Nonlinear System Identification

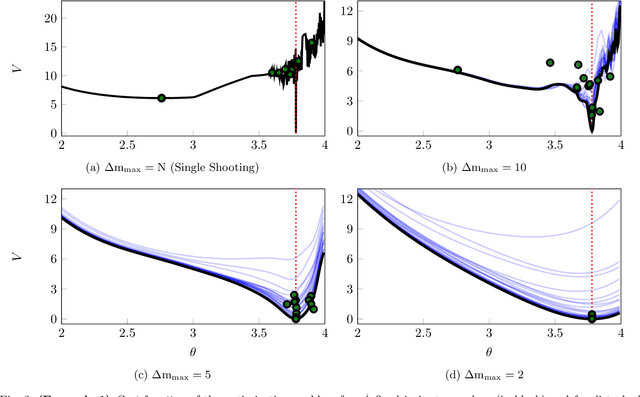
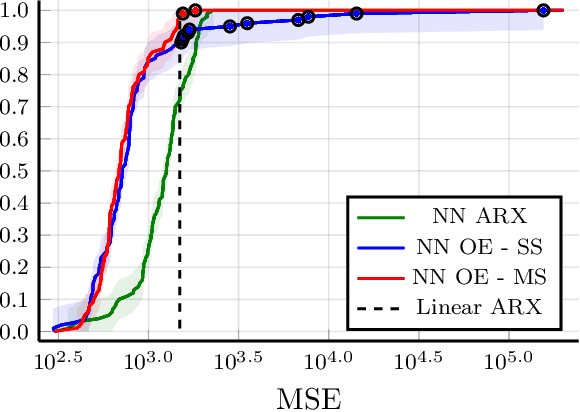
New light is shed onto optimization problems resulting from prediction error parameter estimation of linear and nonlinear systems. It is shown that the smoothness" of the objective function depends both on the simulation length and on the decay rate of the prediction model. More precisely, for regions of the parameter space where the model is not contractive, the Lipschitz constant and $\beta$-smoothness of the objective function might blow up exponentially with the simulation length, making it hard to numerically find minima within those regions or, even, to escape from them. In addition to providing theoretical understanding of this problem, this paper also proposes the use of multiple shooting as a viable solution. The proposed method minimizes the error between a prediction model and observed values. Rather than running the prediction model over the entire dataset, as in the original prediction error formulation, multiple shooting splits the data into smaller subsets and runs the prediction model over each subdivision, making the simulation length a design parameter and making it possible to solve problems that would be infeasible using a standard approach. The equivalence with the original problem is obtained by including constraints in the optimization. The method is illustrated for the parameter estimation of nonlinear systems with chaotic or unstable behavior, as well as on neural network parameter estimation.