NLBAC: A Neural Ordinary Differential Equations-based Framework for Stable and Safe Reinforcement Learning

Reinforcement learning (RL) excels in applications such as video games and robotics, but ensuring safety and stability remains challenging when using RL to control real-world systems where using model-free algorithms suffering from low sample efficiency might be prohibitive. This paper first provides safety and stability definitions for the RL system, and then introduces a Neural ordinary differential equations-based Lyapunov-Barrier Actor-Critic (NLBAC) framework that leverages Neural Ordinary Differential Equations (NODEs) to approximate system dynamics and integrates the Control Barrier Function (CBF) and Control Lyapunov Function (CLF) frameworks with the actor-critic method to assist in maintaining the safety and stability for the system. Within this framework, we employ the augmented Lagrangian method to update the RL-based controller parameters. Additionally, we introduce an extra backup controller in situations where CBF constraints for safety and the CLF constraint for stability cannot be satisfied simultaneously. Simulation results demonstrate that the framework leads the system to approach the desired state and allows fewer violations of safety constraints with better sample efficiency compared to other methods.

A Barrier-Lyapunov Actor-Critic Reinforcement Learning Approach for Safe and Stable Control

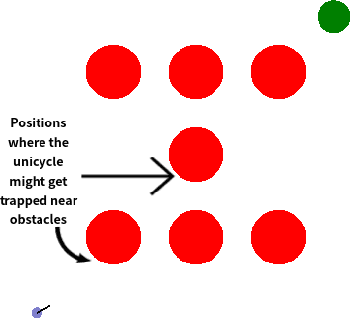
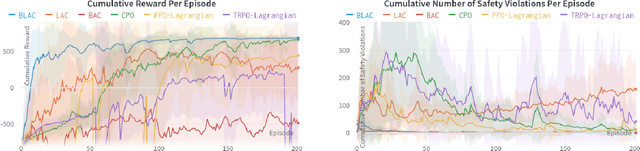
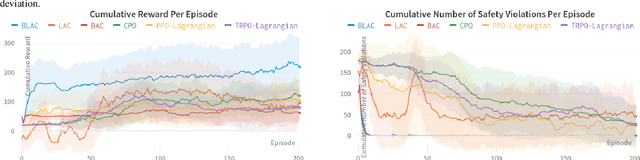
Reinforcement learning (RL) has demonstrated impressive performance in various areas such as video games and robotics. However, ensuring safety and stability, which are two critical properties from a control perspective, remains a significant challenge when using RL to control real-world systems. In this paper, we first provide definitions of safety and stability for the RL system, and then combine the control barrier function (CBF) and control Lyapunov function (CLF) methods with the actor-critic method in RL to propose a Barrier-Lyapunov Actor-Critic (BLAC) framework which helps maintain the aforementioned safety and stability for the system. In this framework, CBF constraints for safety and CLF constraint for stability are constructed based on the data sampled from the replay buffer, and the augmented Lagrangian method is used to update the parameters of the RL-based controller. Furthermore, an additional backup controller is introduced in case the RL-based controller cannot provide valid control signals when safety and stability constraints cannot be satisfied simultaneously. Simulation results show that this framework yields a controller that can help the system approach the desired state and cause fewer violations of safety constraints compared to baseline algorithms.