NLBAC: A Neural Ordinary Differential Equations-based Framework for Stable and Safe Reinforcement Learning

Reinforcement learning (RL) excels in applications such as video games and robotics, but ensuring safety and stability remains challenging when using RL to control real-world systems where using model-free algorithms suffering from low sample efficiency might be prohibitive. This paper first provides safety and stability definitions for the RL system, and then introduces a Neural ordinary differential equations-based Lyapunov-Barrier Actor-Critic (NLBAC) framework that leverages Neural Ordinary Differential Equations (NODEs) to approximate system dynamics and integrates the Control Barrier Function (CBF) and Control Lyapunov Function (CLF) frameworks with the actor-critic method to assist in maintaining the safety and stability for the system. Within this framework, we employ the augmented Lagrangian method to update the RL-based controller parameters. Additionally, we introduce an extra backup controller in situations where CBF constraints for safety and the CLF constraint for stability cannot be satisfied simultaneously. Simulation results demonstrate that the framework leads the system to approach the desired state and allows fewer violations of safety constraints with better sample efficiency compared to other methods.

Rational Neural Network Controllers

Neural networks have shown great success in many machine learning related tasks, due to their ability to act as general function approximators. Recent work has demonstrated the effectiveness of neural networks in control systems (known as neural feedback loops), most notably by using a neural network as a controller. However, one of the big challenges of this approach is that neural networks have been shown to be sensitive to adversarial attacks. This means that, unless they are designed properly, they are not an ideal candidate for controllers due to issues with robustness and uncertainty, which are pivotal aspects of control systems. There has been initial work on robustness to both analyse and design dynamical systems with neural network controllers. However, one prominent issue with these methods is that they use existing neural network architectures tailored for traditional machine learning tasks. These structures may not be appropriate for neural network controllers and it is important to consider alternative architectures. This paper considers rational neural networks and presents novel rational activation functions, which can be used effectively in robustness problems for neural feedback loops. Rational activation functions are replaced by a general rational neural network structure, which is convex in the neural network's parameters. A method is proposed to recover a stabilising controller from a Sum of Squares feasibility test. This approach is then applied to a refined rational neural network which is more compatible with Sum of Squares programming. Numerical examples show that this method can successfully recover stabilising rational neural network controllers for neural feedback loops with non-linear plants with noise and parametric uncertainty.

A Barrier-Lyapunov Actor-Critic Reinforcement Learning Approach for Safe and Stable Control

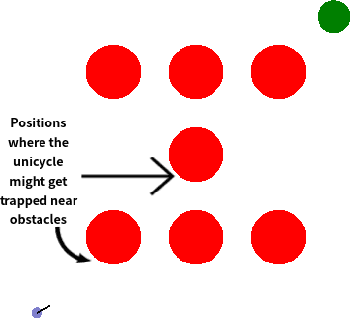
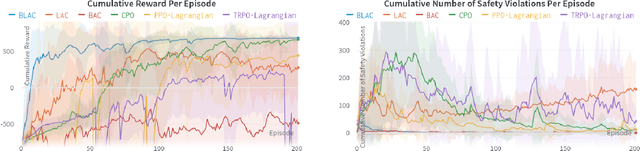
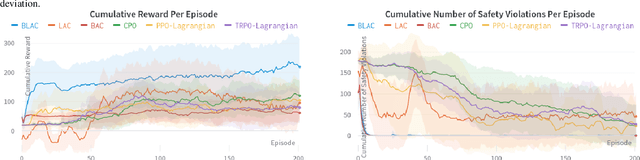
Reinforcement learning (RL) has demonstrated impressive performance in various areas such as video games and robotics. However, ensuring safety and stability, which are two critical properties from a control perspective, remains a significant challenge when using RL to control real-world systems. In this paper, we first provide definitions of safety and stability for the RL system, and then combine the control barrier function (CBF) and control Lyapunov function (CLF) methods with the actor-critic method in RL to propose a Barrier-Lyapunov Actor-Critic (BLAC) framework which helps maintain the aforementioned safety and stability for the system. In this framework, CBF constraints for safety and CLF constraint for stability are constructed based on the data sampled from the replay buffer, and the augmented Lagrangian method is used to update the parameters of the RL-based controller. Furthermore, an additional backup controller is introduced in case the RL-based controller cannot provide valid control signals when safety and stability constraints cannot be satisfied simultaneously. Simulation results show that this framework yields a controller that can help the system approach the desired state and cause fewer violations of safety constraints compared to baseline algorithms.

Stochastic processes and feedback-linearisation for online identification and Bayesian adaptive control of fully-actuated mechanical systems

This work proposes a new method for simultaneous probabilistic identification and control of an observable, fully-actuated mechanical system. Identification is achieved by conditioning stochastic process priors on observations of configurations and noisy estimates of configuration derivatives. In contrast to previous work that has used stochastic processes for identification, we leverage the structural knowledge afforded by Lagrangian mechanics and learn the drift and control input matrix functions of the control-affine system separately. We utilise feedback-linearisation to reduce, in expectation, the uncertain nonlinear control problem to one that is easy to regulate in a desired manner. Thereby, our method combines the flexibility of nonparametric Bayesian learning with epistemological guarantees on the expected closed-loop trajectory. We illustrate our method in the context of torque-actuated pendula where the dynamics are learned with a combination of normal and log-normal processes.