NLBAC: A Neural Ordinary Differential Equations-based Framework for Stable and Safe Reinforcement Learning

Reinforcement learning (RL) excels in applications such as video games and robotics, but ensuring safety and stability remains challenging when using RL to control real-world systems where using model-free algorithms suffering from low sample efficiency might be prohibitive. This paper first provides safety and stability definitions for the RL system, and then introduces a Neural ordinary differential equations-based Lyapunov-Barrier Actor-Critic (NLBAC) framework that leverages Neural Ordinary Differential Equations (NODEs) to approximate system dynamics and integrates the Control Barrier Function (CBF) and Control Lyapunov Function (CLF) frameworks with the actor-critic method to assist in maintaining the safety and stability for the system. Within this framework, we employ the augmented Lagrangian method to update the RL-based controller parameters. Additionally, we introduce an extra backup controller in situations where CBF constraints for safety and the CLF constraint for stability cannot be satisfied simultaneously. Simulation results demonstrate that the framework leads the system to approach the desired state and allows fewer violations of safety constraints with better sample efficiency compared to other methods.

Learning Robust State Observers using Neural ODEs (longer version)

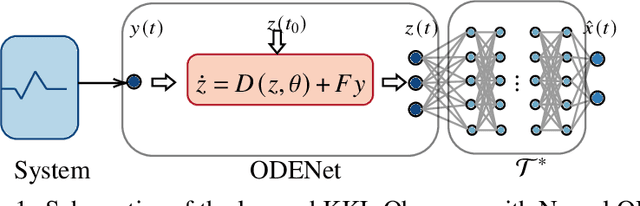
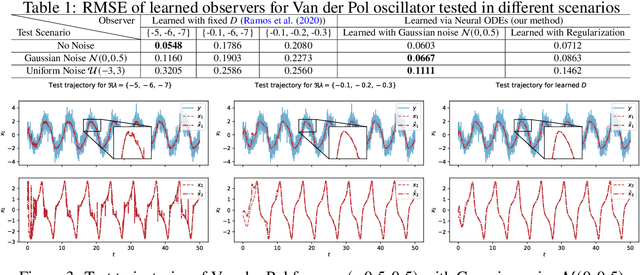
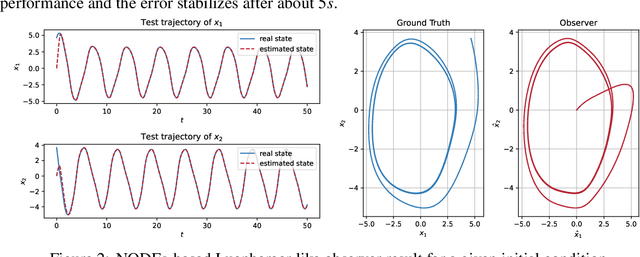
Relying on recent research results on Neural ODEs, this paper presents a methodology for the design of state observers for nonlinear systems based on Neural ODEs, learning Luenberger-like observers and their nonlinear extension (Kazantzis-Kravaris-Luenberger (KKL) observers) for systems with partially-known nonlinear dynamics and fully unknown nonlinear dynamics, respectively. In particular, for tuneable KKL observers, the relationship between the design of the observer and its trade-off between convergence speed and robustness is analysed and used as a basis for improving the robustness of the learning-based observer in training. We illustrate the advantages of this approach in numerical simulations.