Walking the Values in Bayesian Inverse Reinforcement Learning

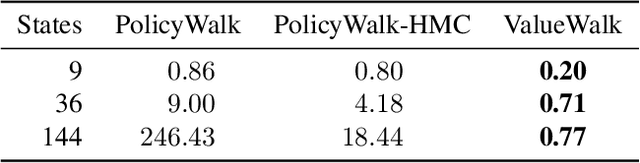
The goal of Bayesian inverse reinforcement learning (IRL) is recovering a posterior distribution over reward functions using a set of demonstrations from an expert optimizing for a reward unknown to the learner. The resulting posterior over rewards can then be used to synthesize an apprentice policy that performs well on the same or a similar task. A key challenge in Bayesian IRL is bridging the computational gap between the hypothesis space of possible rewards and the likelihood, often defined in terms of Q values: vanilla Bayesian IRL needs to solve the costly forward planning problem - going from rewards to the Q values - at every step of the algorithm, which may need to be done thousands of times. We propose to solve this by a simple change: instead of focusing on primarily sampling in the space of rewards, we can focus on primarily working in the space of Q-values, since the computation required to go from Q-values to reward is radically cheaper. Furthermore, this reversion of the computation makes it easy to compute the gradient allowing efficient sampling using Hamiltonian Monte Carlo. We propose ValueWalk - a new Markov chain Monte Carlo method based on this insight - and illustrate its advantages on several tasks.

NLBAC: A Neural Ordinary Differential Equations-based Framework for Stable and Safe Reinforcement Learning

Reinforcement learning (RL) excels in applications such as video games and robotics, but ensuring safety and stability remains challenging when using RL to control real-world systems where using model-free algorithms suffering from low sample efficiency might be prohibitive. This paper first provides safety and stability definitions for the RL system, and then introduces a Neural ordinary differential equations-based Lyapunov-Barrier Actor-Critic (NLBAC) framework that leverages Neural Ordinary Differential Equations (NODEs) to approximate system dynamics and integrates the Control Barrier Function (CBF) and Control Lyapunov Function (CLF) frameworks with the actor-critic method to assist in maintaining the safety and stability for the system. Within this framework, we employ the augmented Lagrangian method to update the RL-based controller parameters. Additionally, we introduce an extra backup controller in situations where CBF constraints for safety and the CLF constraint for stability cannot be satisfied simultaneously. Simulation results demonstrate that the framework leads the system to approach the desired state and allows fewer violations of safety constraints with better sample efficiency compared to other methods.

A Barrier-Lyapunov Actor-Critic Reinforcement Learning Approach for Safe and Stable Control

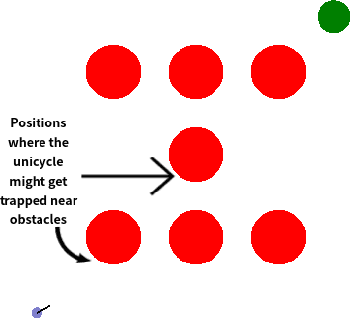
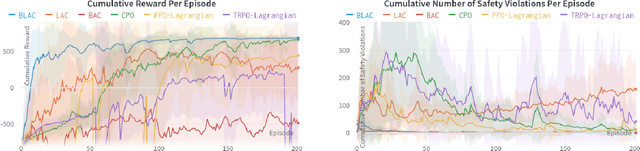
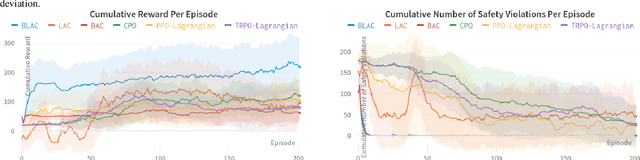
Reinforcement learning (RL) has demonstrated impressive performance in various areas such as video games and robotics. However, ensuring safety and stability, which are two critical properties from a control perspective, remains a significant challenge when using RL to control real-world systems. In this paper, we first provide definitions of safety and stability for the RL system, and then combine the control barrier function (CBF) and control Lyapunov function (CLF) methods with the actor-critic method in RL to propose a Barrier-Lyapunov Actor-Critic (BLAC) framework which helps maintain the aforementioned safety and stability for the system. In this framework, CBF constraints for safety and CLF constraint for stability are constructed based on the data sampled from the replay buffer, and the augmented Lagrangian method is used to update the parameters of the RL-based controller. Furthermore, an additional backup controller is introduced in case the RL-based controller cannot provide valid control signals when safety and stability constraints cannot be satisfied simultaneously. Simulation results show that this framework yields a controller that can help the system approach the desired state and cause fewer violations of safety constraints compared to baseline algorithms.

Learning Robust State Observers using Neural ODEs (longer version)

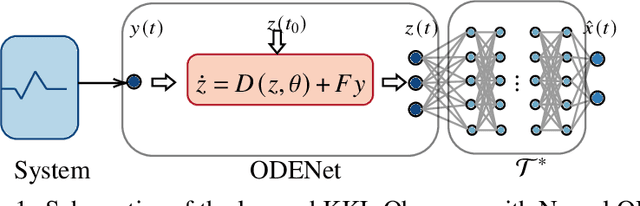
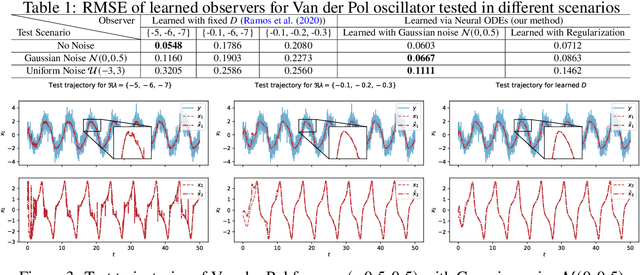
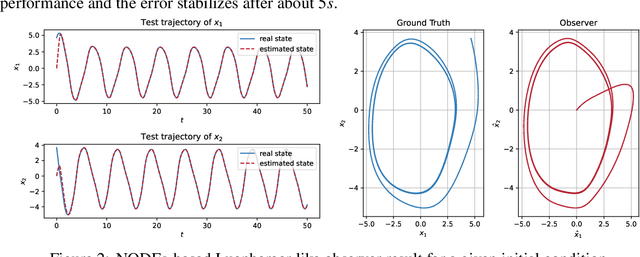
Relying on recent research results on Neural ODEs, this paper presents a methodology for the design of state observers for nonlinear systems based on Neural ODEs, learning Luenberger-like observers and their nonlinear extension (Kazantzis-Kravaris-Luenberger (KKL) observers) for systems with partially-known nonlinear dynamics and fully unknown nonlinear dynamics, respectively. In particular, for tuneable KKL observers, the relationship between the design of the observer and its trade-off between convergence speed and robustness is analysed and used as a basis for improving the robustness of the learning-based observer in training. We illustrate the advantages of this approach in numerical simulations.

Graph Reinforcement Learning for Wireless Control Systems: Large-Scale Resource Allocation over Interference Channels

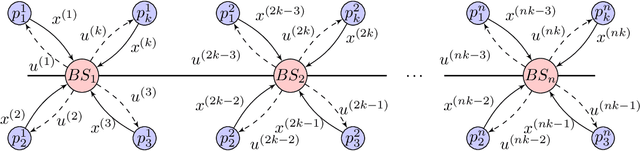
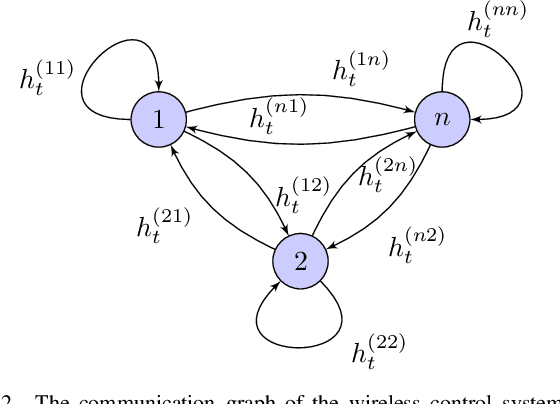
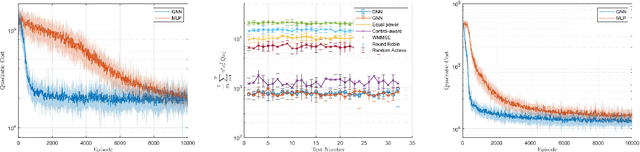
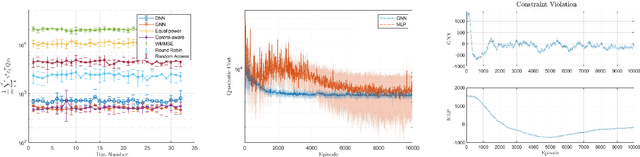
Modern control systems routinely employ wireless networks to exchange information between spatially distributed plants, actuators and sensors. With wireless networks defined by random, rapidly changing transmission conditions that challenge assumptions commonly held in the design of control systems, proper allocation of communication resources is essential to achieve reliable operation. Designing resource allocation policies, however, is challenging, motivating recent works to successfully exploit deep learning and deep reinforcement learning techniques to design resource allocation and scheduling policies for wireless control systems. As the number of learnable parameters in a neural network grows with the size of the input signal, deep reinforcement learning algorithms may fail to scale, limiting the immediate generalization of such scheduling and resource allocation policies to large-scale systems. The interference and fading patterns among plants and controllers in the network, on the other hand, induce a time-varying communication graph that can be used to construct policy representations based on graph neural networks (GNNs), with the number of learnable parameters now independent of the number of plants in the network. That invariance to the number of nodes is key to design scalable and transferable resource allocation policies, which can be trained with reinforcement learning. Through extensive numerical experiments we show that the proposed graph reinforcement learning approach yields policies that not only outperform baseline solutions and deep reinforcement learning based policies in large-scale systems, but that can also be transferred across networks of varying size.

Federated Reinforcement Learning at the Edge

Modern cyber-physical architectures use data collected from systems at different physical locations to learn appropriate behaviors and adapt to uncertain environments. However, an important challenge arises as communication exchanges at the edge of networked systems are costly due to limited resources. This paper considers a setup where multiple agents need to communicate efficiently in order to jointly solve a reinforcement learning problem over time-series data collected in a distributed manner. This is posed as learning an approximate value function over a communication network. An algorithm for achieving communication efficiency is proposed, supported with theoretical guarantees, practical implementations, and numerical evaluations. The approach is based on the idea of communicating only when sufficiently informative data is collected.

Linear Regression over Networks with Communication Guarantees

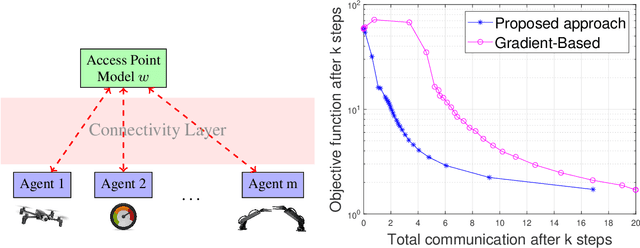
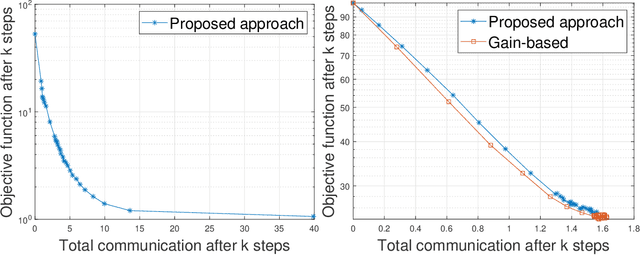
A key functionality of emerging connected autonomous systems such as smart cities, smart transportation systems, and the industrial Internet-of-Things, is the ability to process and learn from data collected at different physical locations. This is increasingly attracting attention under the terms of distributed learning and federated learning. However, in connected autonomous systems, data transfer takes place over communication networks with often limited resources. This paper examines algorithms for communication-efficient learning for linear regression tasks by exploiting the informativeness of the data. The developed algorithms enable a tradeoff between communication and learning with theoretical performance guarantees and efficient practical implementations.

Adaptive Scheduling for Machine Learning Tasks over Networks

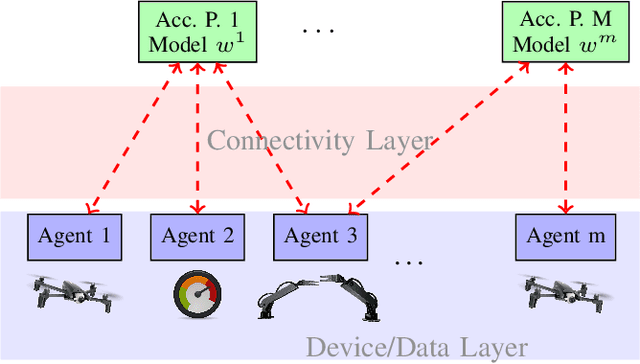
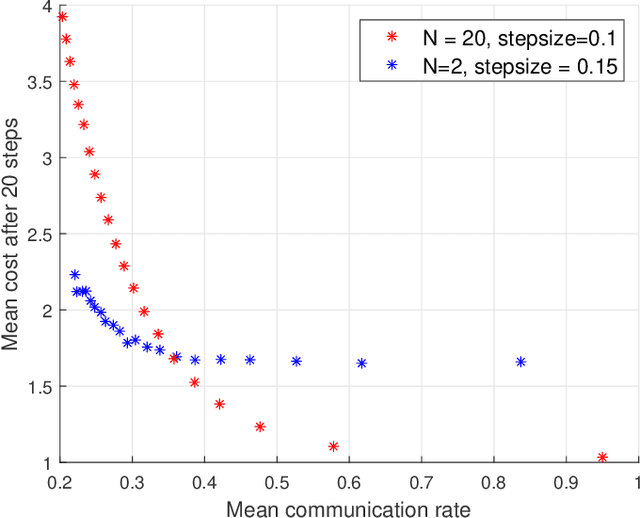
A key functionality of emerging connected autonomous systems such as smart transportation systems, smart cities, and the industrial Internet-of-Things, is the ability to process and learn from data collected at different physical locations. This is increasingly attracting attention under the terms of distributed learning and federated learning. However, in this setup data transfer takes place over communication resources that are shared among many users and tasks or subject to capacity constraints. This paper examines algorithms for efficiently allocating resources to linear regression tasks by exploiting the informativeness of the data. The algorithms developed enable adaptive scheduling of learning tasks with reliable performance guarantees.

Statistical Learning for Analysis of Networked Control Systems over Unknown Channels

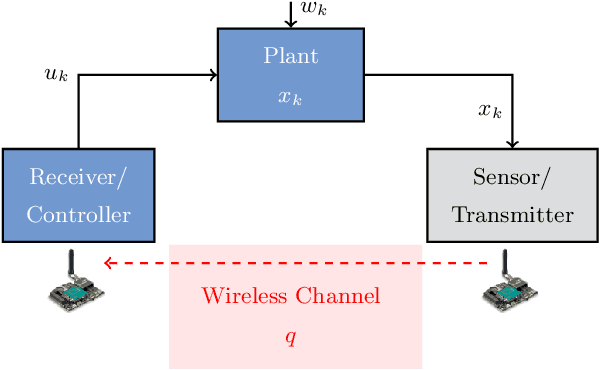
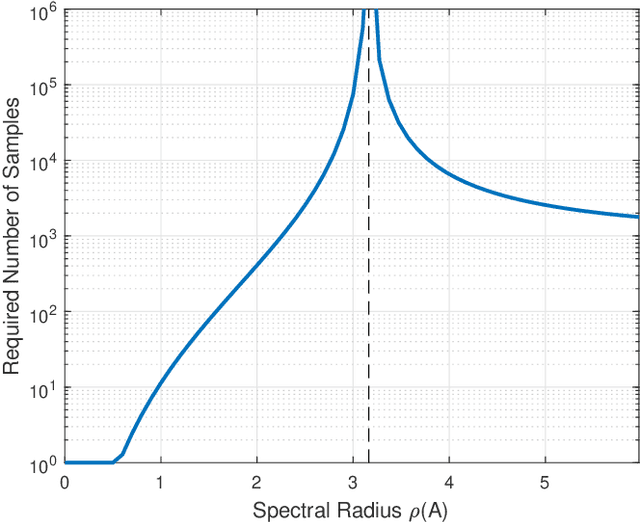
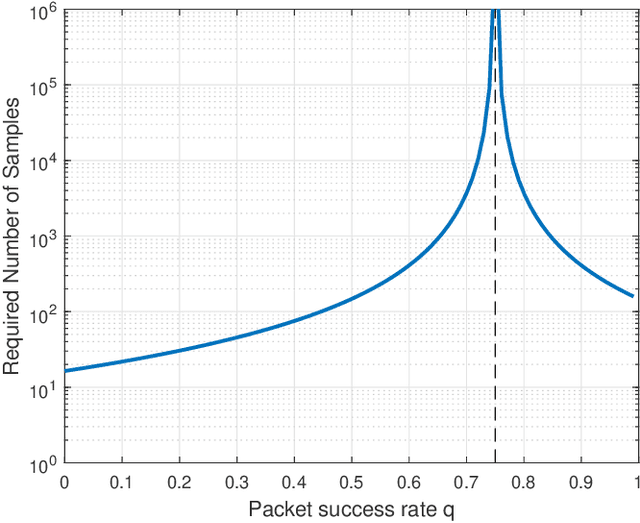
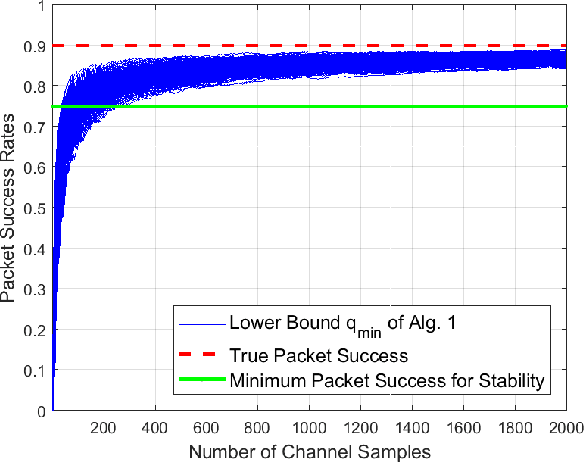
Recent control trends are increasingly relying on communication networks and wireless channels to close the loop for Internet-of-Things applications. Traditionally these approaches are model-based, i.e., assuming a network or channel model they are focused on stability analysis and appropriate controller designs. However the availability of such wireless channel modeling is fundamentally challenging in practice as channels are typically unknown a priori and only available through data samples. In this work we aim to develop algorithms that rely on channel sample data to determine the stability and performance of networked control tasks. In this regard our work is the first to characterize the amount of channel modeling that is required to answer such a question. Specifically we examine how many channel data samples are required in order to answer with high confidence whether a given networked control system is stable or not. This analysis is based on the notion of sample complexity from the learning literature and is facilitated by concentration inequalities. Moreover we establish a direct relation between the sample complexity and the networked system stability margin, i.e., the underlying packet success rate of the channel and the spectral radius of the dynamics of the control system. This illustrates that it becomes impractical to verify stability under a large range of plant and channel configurations. We validate our theoretical results in numerical simulations.