Håkan Hjalmarsson
Bayes and Biased Estimators Without Hyper-parameter Estimation: Comparable Performance to the Empirical-Bayes-Based Regularized Estimator
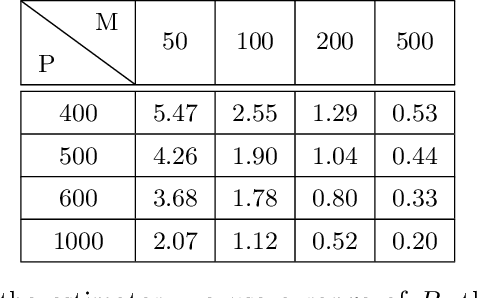
Mar 14, 2025Abstract:Regularized system identification has become a significant complement to more classical system identification. It has been numerically shown that kernel-based regularized estimators often perform better than the maximum likelihood estimator in terms of minimizing mean squared error (MSE). However, regularized estimators often require hyper-parameter estimation. This paper focuses on ridge regression and the regularized estimator by employing the empirical Bayes hyper-parameter estimator. We utilize the excess MSE to quantify the MSE difference between the empirical-Bayes-based regularized estimator and the maximum likelihood estimator for large sample sizes. We then exploit the excess MSE expressions to develop both a family of generalized Bayes estimators and a family of closed-form biased estimators. They have the same excess MSE as the empirical-Bayes-based regularized estimator but eliminate the need for hyper-parameter estimation. Moreover, we conduct numerical simulations to show that the performance of these new estimators is comparable to the empirical-Bayes-based regularized estimator, while computationally, they are more efficient.
DeepBayes -- an estimator for parameter estimation in stochastic nonlinear dynamical models
May 04, 2022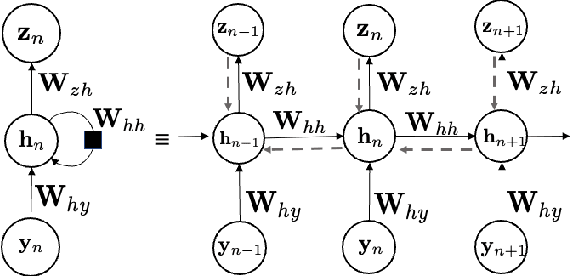

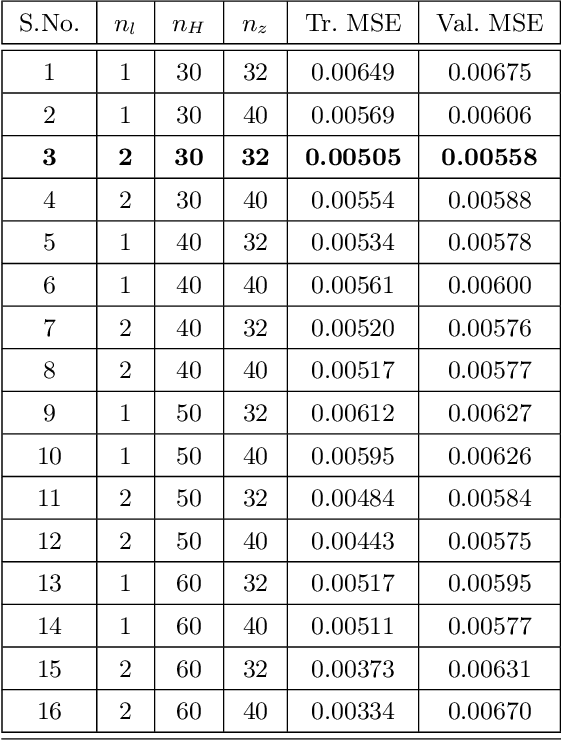
Abstract:Stochastic nonlinear dynamical systems are ubiquitous in modern, real-world applications. Yet, estimating the unknown parameters of stochastic, nonlinear dynamical models remains a challenging problem. The majority of existing methods employ maximum likelihood or Bayesian estimation. However, these methods suffer from some limitations, most notably the substantial computational time for inference coupled with limited flexibility in application. In this work, we propose DeepBayes estimators that leverage the power of deep recurrent neural networks in learning an estimator. The method consists of first training a recurrent neural network to minimize the mean-squared estimation error over a set of synthetically generated data using models drawn from the model set of interest. The a priori trained estimator can then be used directly for inference by evaluating the network with the estimation data. The deep recurrent neural network architectures can be trained offline and ensure significant time savings during inference. We experiment with two popular recurrent neural networks -- long short term memory network (LSTM) and gated recurrent unit (GRU). We demonstrate the applicability of our proposed method on different example models and perform detailed comparisons with state-of-the-art approaches. We also provide a study on a real-world nonlinear benchmark problem. The experimental evaluations show that the proposed approach is asymptotically as good as the Bayes estimator.
Learning sparse linear dynamic networks in a hyper-parameter free setting
Nov 26, 2019

Abstract:We address the issue of estimating the topology and dynamics of sparse linear dynamic networks in a hyperparameter-free setting. We propose a method to estimate the network dynamics in a computationally efficient and parameter tuning-free iterative framework known as SPICE (Sparse Iterative Covariance Estimation). The estimated dynamics directly reveal the underlying topology. Our approach does not assume that the network is undirected and is applicable even with varying noise levels across the modules of the network. We also do not assume any explicit prior knowledge on the network dynamics. Numerical experiments with realistic dynamic networks illustrate the usefulness of our method.
Robust exploration in linear quadratic reinforcement learning
Jun 04, 2019



Abstract:This paper concerns the problem of learning control policies for an unknown linear dynamical system to minimize a quadratic cost function. We present a method, based on convex optimization, that accomplishes this task robustly: i.e., we minimize the worst-case cost, accounting for system uncertainty given the observed data. The method balances exploitation and exploration, exciting the system in such a way so as to reduce uncertainty in the model parameters to which the worst-case cost is most sensitive. Numerical simulations and application to a hardware-in-the-loop servo-mechanism demonstrate the approach, with appreciable performance and robustness gains over alternative methods observed in both.
A new kernel-based approach to system identification with quantized output data
Jun 20, 2017
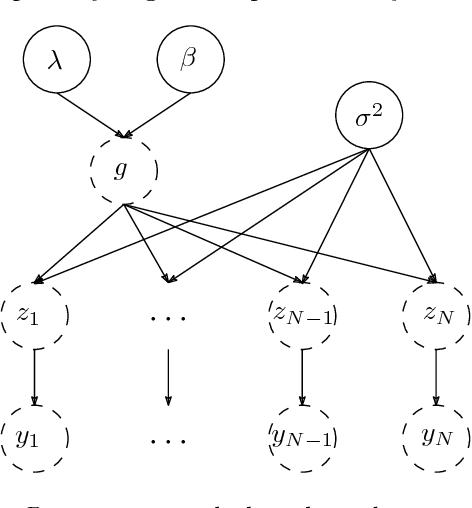
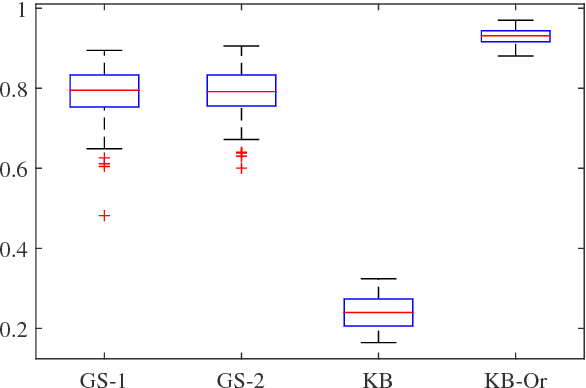
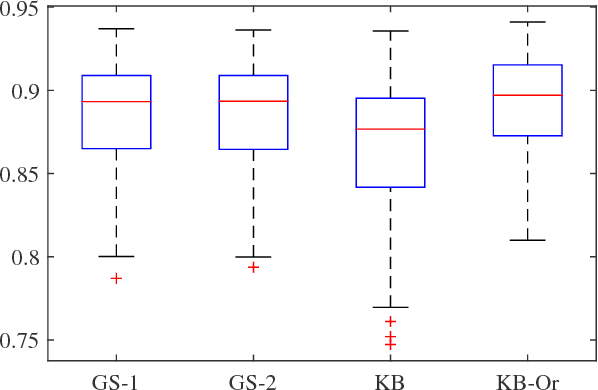
Abstract:In this paper we introduce a novel method for linear system identification with quantized output data. We model the impulse response as a zero-mean Gaussian process whose covariance (kernel) is given by the recently proposed stable spline kernel, which encodes information on regularity and exponential stability. This serves as a starting point to cast our system identification problem into a Bayesian framework. We employ Markov Chain Monte Carlo methods to provide an estimate of the system. In particular, we design two methods based on the so-called Gibbs sampler that allow also to estimate the kernel hyperparameters by marginal likelihood maximization via the expectation-maximization method. Numerical simulations show the effectiveness of the proposed scheme, as compared to the state-of-the-art kernel-based methods when these are employed in system identification with quantized data.
Blind system identification using kernel-based methods
May 19, 2016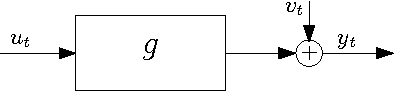
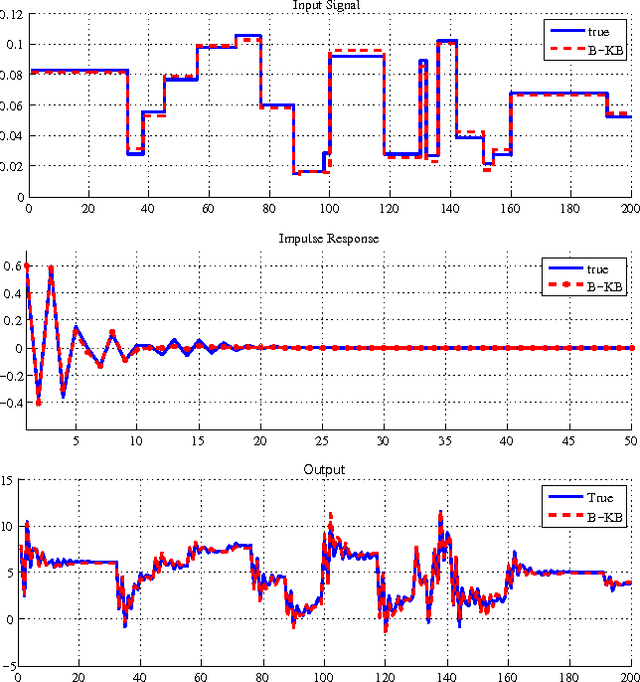
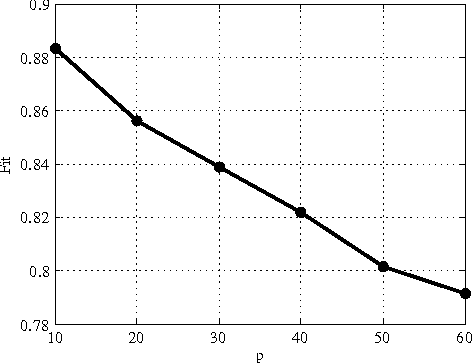
Abstract:We propose a new method for blind system identification. Resorting to a Gaussian regression framework, we model the impulse response of the unknown linear system as a realization of a Gaussian process. The structure of the covariance matrix (or kernel) of such a process is given by the stable spline kernel, which has been recently introduced for system identification purposes and depends on an unknown hyperparameter. We assume that the input can be linearly described by few parameters. We estimate these parameters, together with the kernel hyperparameter and the noise variance, using an empirical Bayes approach. The related optimization problem is efficiently solved with a novel iterative scheme based on the Expectation-Maximization method. In particular, we show that each iteration consists of a set of simple update rules. We show, through some numerical experiments, very promising performance of the proposed method.
On the estimation of initial conditions in kernel-based system identification
May 19, 2016
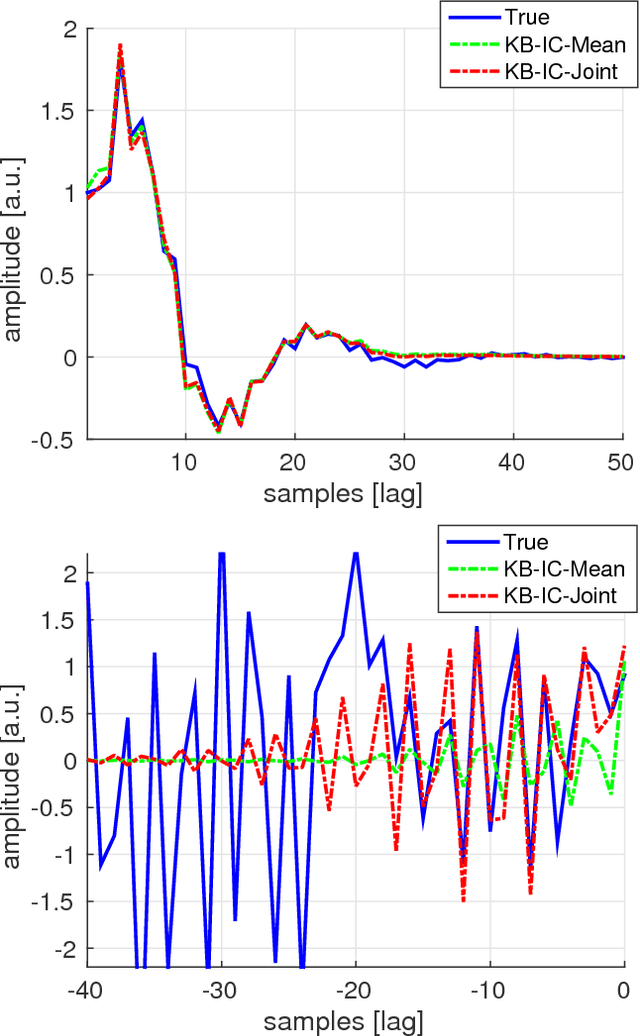
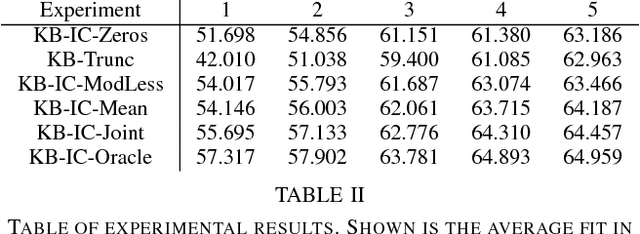
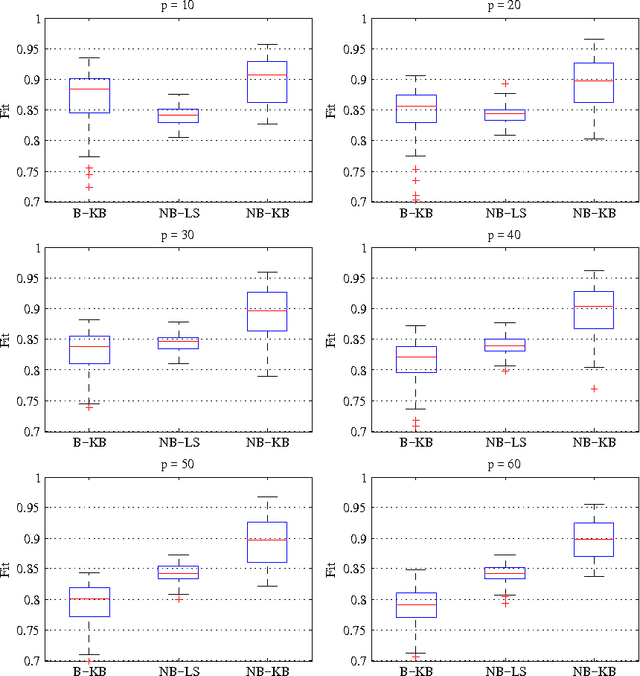
Abstract:Recent developments in system identification have brought attention to regularized kernel-based methods, where, adopting the recently introduced stable spline kernel, prior information on the unknown process is enforced. This reduces the variance of the estimates and thus makes kernel-based methods particularly attractive when few input-output data samples are available. In such cases however, the influence of the system initial conditions may have a significant impact on the output dynamics. In this paper, we specifically address this point. We propose three methods that deal with the estimation of initial conditions using different types of information. The methods consist in various mixed maximum likelihood--a posteriori estimators which estimate the initial conditions and tune the hyperparameters characterizing the stable spline kernel. To solve the related optimization problems, we resort to the expectation-maximization method, showing that the solutions can be attained by iterating among simple update steps. Numerical experiments show the advantages, in terms of accuracy in reconstructing the system impulse response, of the proposed strategies, compared to other kernel-based schemes not accounting for the effect initial conditions.
A new kernel-based approach for overparameterized Hammerstein system identification
May 18, 2016
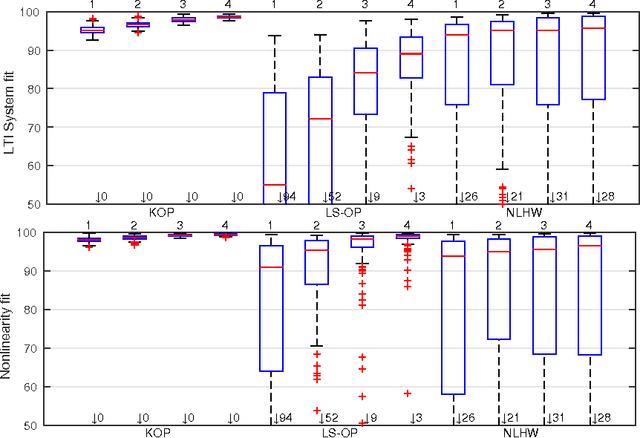
Abstract:In this paper we propose a new identification scheme for Hammerstein systems, which are dynamic systems consisting of a static nonlinearity and a linear time-invariant dynamic system in cascade. We assume that the nonlinear function can be described as a linear combination of $p$ basis functions. We reconstruct the $p$ coefficients of the nonlinearity together with the first $n$ samples of the impulse response of the linear system by estimating an $np$-dimensional overparameterized vector, which contains all the combinations of the unknown variables. To avoid high variance in these estimates, we adopt a regularized kernel-based approach and, in particular, we introduce a new kernel tailored for Hammerstein system identification. We show that the resulting scheme provides an estimate of the overparameterized vector that can be uniquely decomposed as the combination of an impulse response and $p$ coefficients of the static nonlinearity. We also show, through several numerical experiments, that the proposed method compares very favorably with two standard methods for Hammerstein system identification.
Robust EM kernel-based methods for linear system identification
Jan 07, 2016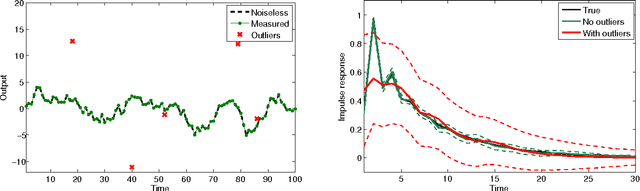
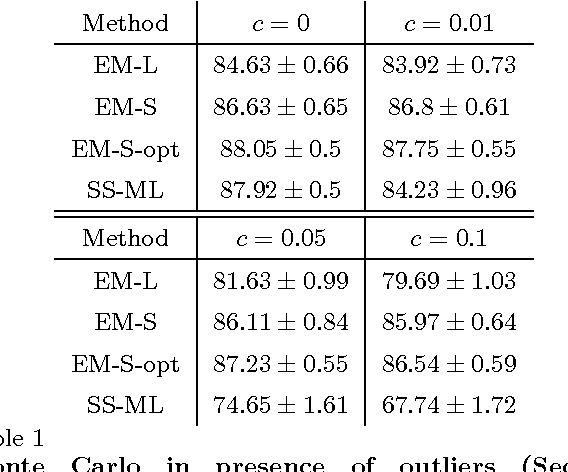

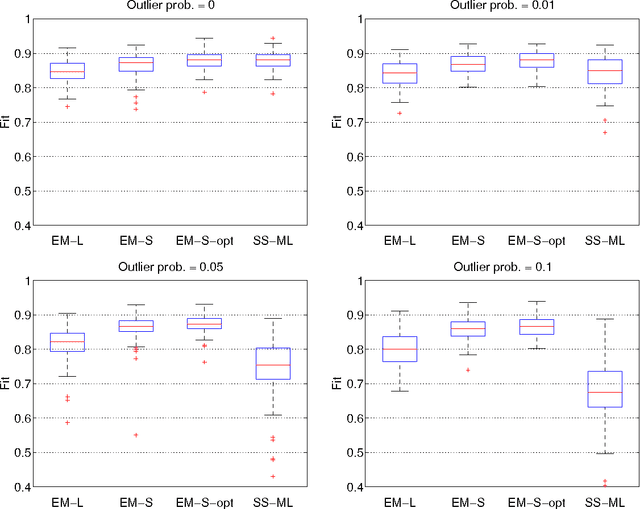
Abstract:Recent developments in system identification have brought attention to regularized kernel-based methods. This type of approach has been proven to compare favorably with classic parametric methods. However, current formulations are not robust with respect to outliers. In this paper, we introduce a novel method to robustify kernel-based system identification methods. To this end, we model the output measurement noise using random variables with heavy-tailed probability density functions (pdfs), focusing on the Laplacian and the Student's t distributions. Exploiting the representation of these pdfs as scale mixtures of Gaussians, we cast our system identification problem into a Gaussian process regression framework, which requires estimating a number of hyperparameters of the data size order. To overcome this difficulty, we design a new maximum a posteriori (MAP) estimator of the hyperparameters, and solve the related optimization problem with a novel iterative scheme based on the Expectation-Maximization (EM) method. In presence of outliers, tests on simulated data and on a real system show a substantial performance improvement compared to currently used kernel-based methods for linear system identification.
Bayesian kernel-based system identification with quantized output data
Apr 26, 2015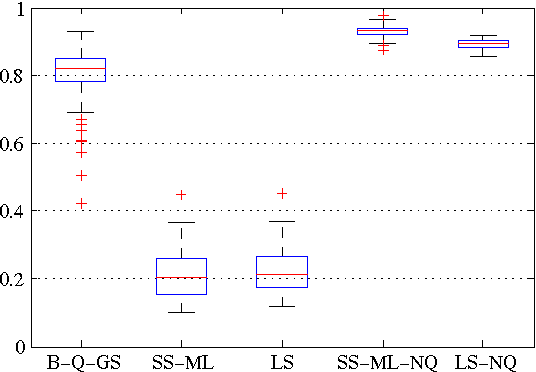
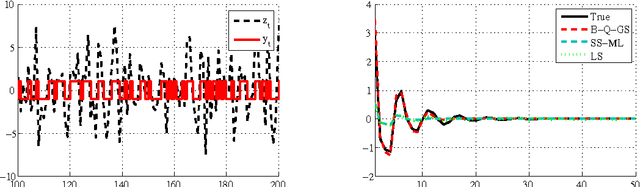
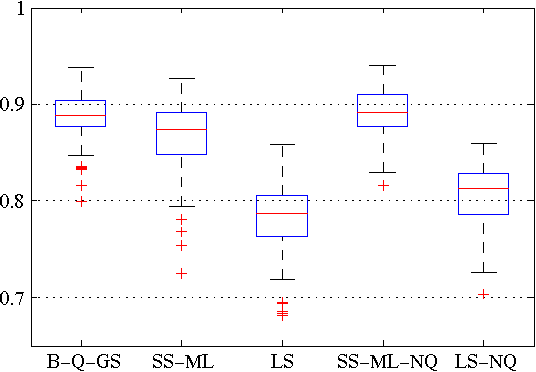
Abstract:In this paper we introduce a novel method for linear system identification with quantized output data. We model the impulse response as a zero-mean Gaussian process whose covariance (kernel) is given by the recently proposed stable spline kernel, which encodes information on regularity and exponential stability. This serves as a starting point to cast our system identification problem into a Bayesian framework. We employ Markov Chain Monte Carlo (MCMC) methods to provide an estimate of the system. In particular, we show how to design a Gibbs sampler which quickly converges to the target distribution. Numerical simulations show a substantial improvement in the accuracy of the estimates over state-of-the-art kernel-based methods when employed in identification of systems with quantized data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge