Riccardo S. Risuleo
Blind system identification using kernel-based methods
May 19, 2016
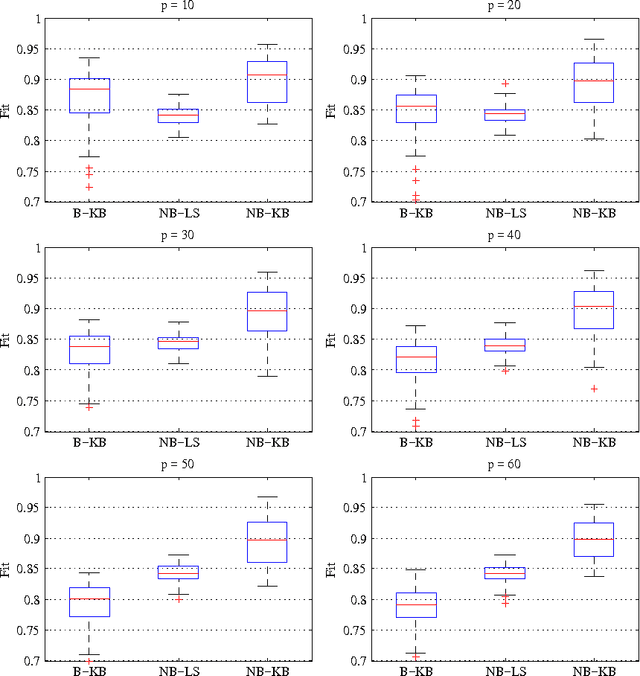
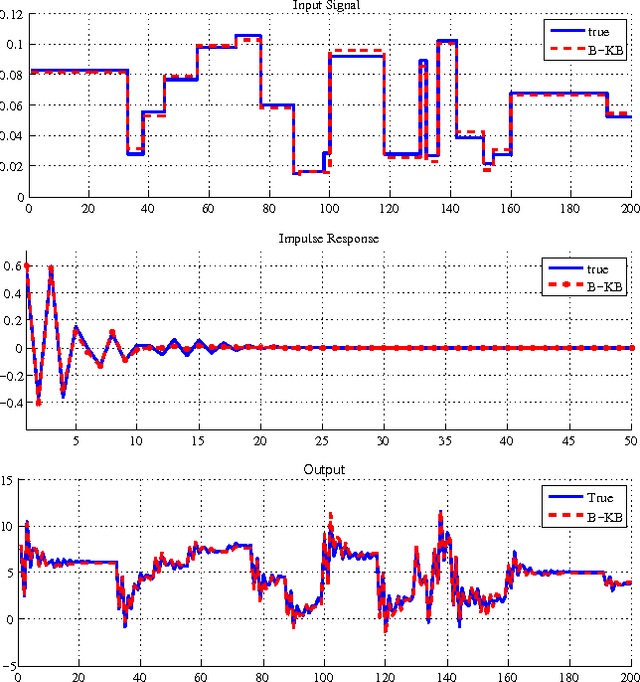
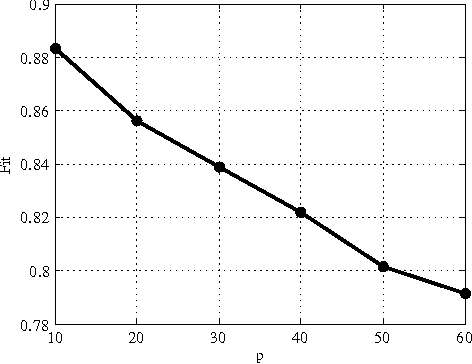
Abstract:We propose a new method for blind system identification. Resorting to a Gaussian regression framework, we model the impulse response of the unknown linear system as a realization of a Gaussian process. The structure of the covariance matrix (or kernel) of such a process is given by the stable spline kernel, which has been recently introduced for system identification purposes and depends on an unknown hyperparameter. We assume that the input can be linearly described by few parameters. We estimate these parameters, together with the kernel hyperparameter and the noise variance, using an empirical Bayes approach. The related optimization problem is efficiently solved with a novel iterative scheme based on the Expectation-Maximization method. In particular, we show that each iteration consists of a set of simple update rules. We show, through some numerical experiments, very promising performance of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge