Learning linear modules in a dynamic network with missing node observations

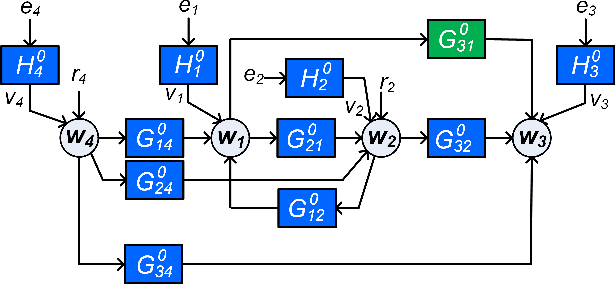
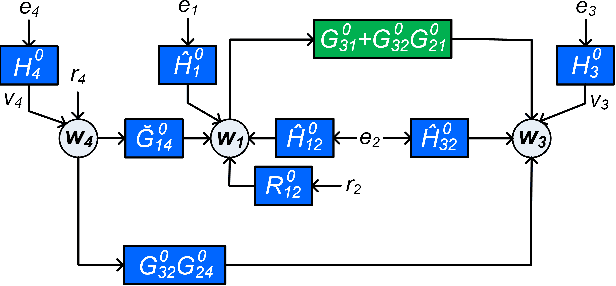
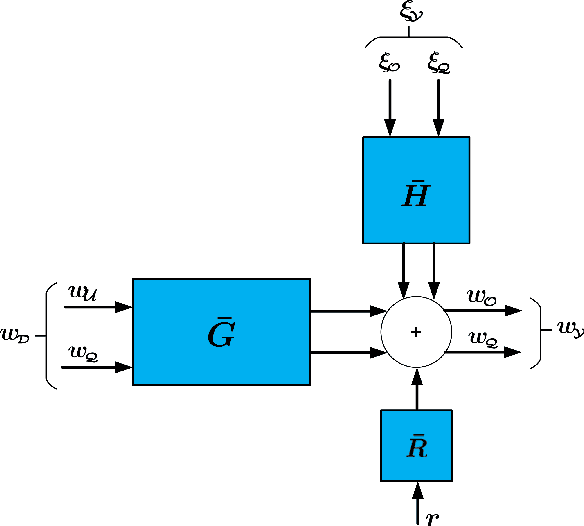
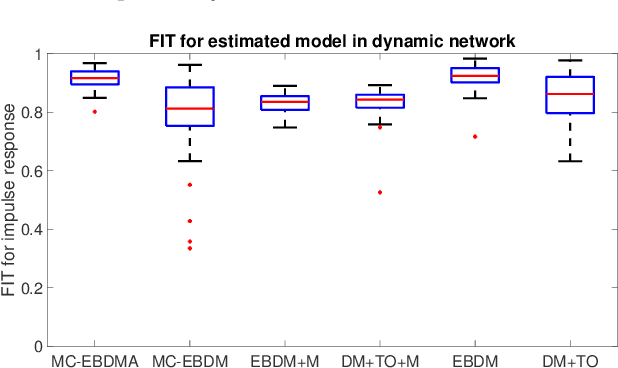
In order to identify a system (module) embedded in a dynamic network, one has to formulate a multiple-input estimation problem that necessitates certain nodes to be measured and included as predictor inputs. However, some of these nodes may not be measurable in many practical cases due to sensor selection and placement issues. This may result in biased estimates of the target module. Furthermore, the identification problem associated with the multiple-input structure may require determining a large number of parameters that are not of particular interest to the experimenter, with increased computational complexity in large-sized networks. In this paper, we tackle these problems by using a data augmentation strategy that allows us to reconstruct the missing node measurements and increase the accuracy of the estimated target module. To this end, we develop a system identification method using regularized kernel-based methods coupled with approximate inference methods. Keeping a parametric model for the module of interest, we model the other modules as Gaussian Processes (GP) with a kernel given by the so-called stable spline kernel. An Empirical Bayes (EB) approach is used to estimate the parameters of the target module. The related optimization problem is solved using an Expectation-Maximization (EM) method, where we employ a Markov-chain Monte Carlo (MCMC) technique to reconstruct the unknown missing node information and the network dynamics. Numerical simulations on dynamic network examples illustrate the potentials of the developed method.

A new kernel-based approach to system identification with quantized output data

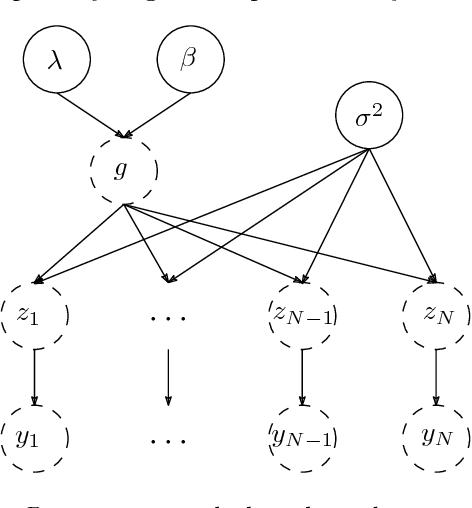
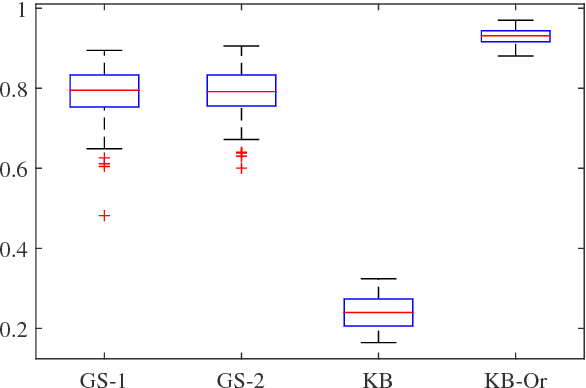
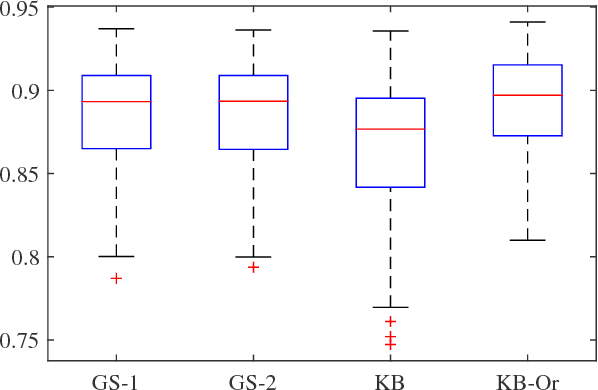
In this paper we introduce a novel method for linear system identification with quantized output data. We model the impulse response as a zero-mean Gaussian process whose covariance (kernel) is given by the recently proposed stable spline kernel, which encodes information on regularity and exponential stability. This serves as a starting point to cast our system identification problem into a Bayesian framework. We employ Markov Chain Monte Carlo methods to provide an estimate of the system. In particular, we design two methods based on the so-called Gibbs sampler that allow also to estimate the kernel hyperparameters by marginal likelihood maximization via the expectation-maximization method. Numerical simulations show the effectiveness of the proposed scheme, as compared to the state-of-the-art kernel-based methods when these are employed in system identification with quantized data.

The Generalized Cross Validation Filter

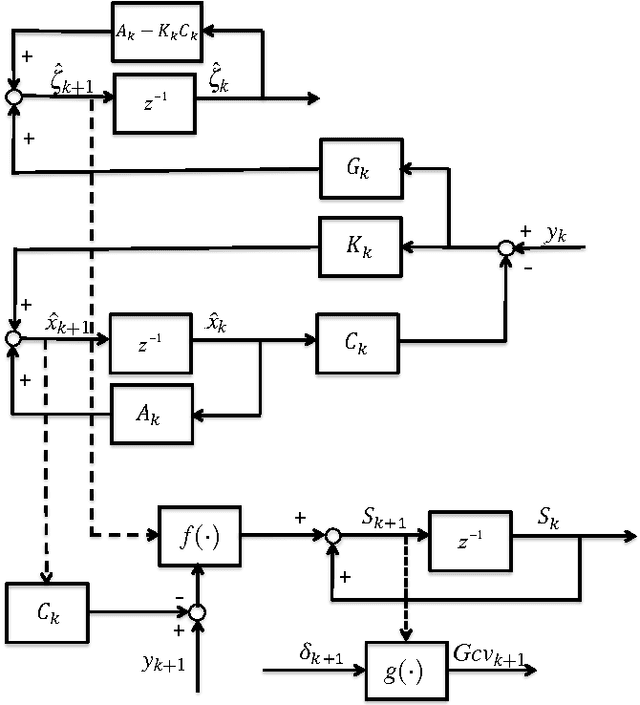
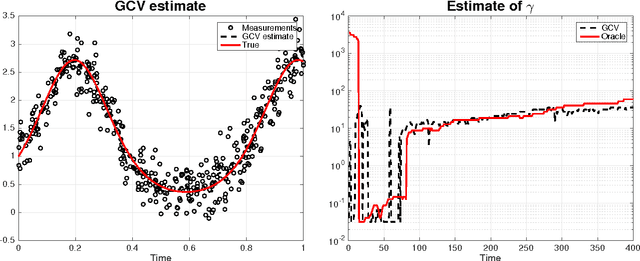
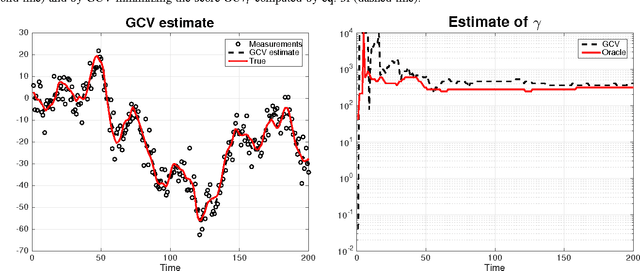
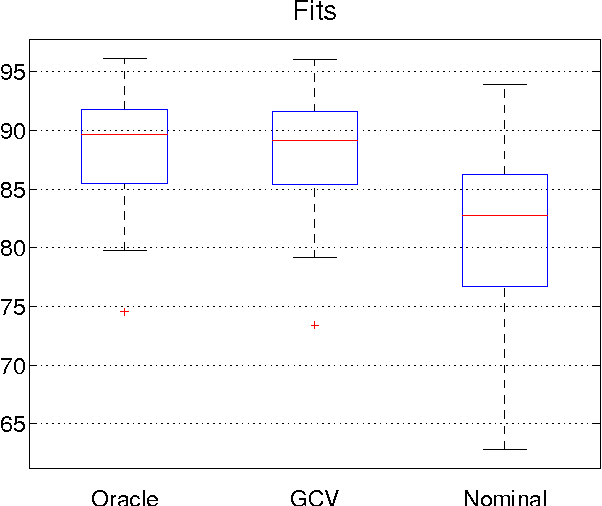
Generalized cross validation (GCV) is one of the most important approaches used to estimate parameters in the context of inverse problems and regularization techniques. A notable example is the determination of the smoothness parameter in splines. When the data are generated by a state space model, like in the spline case, efficient algorithms are available to evaluate the GCV score with complexity that scales linearly in the data set size. However, these methods are not amenable to on-line applications since they rely on forward and backward recursions. Hence, if the objective has been evaluated at time $t-1$ and new data arrive at time t, then O(t) operations are needed to update the GCV score. In this paper we instead show that the update cost is $O(1)$, thus paving the way to the on-line use of GCV. This result is obtained by deriving the novel GCV filter which extends the classical Kalman filter equations to efficiently propagate the GCV score over time. We also illustrate applications of the new filter in the context of state estimation and on-line regularized linear system identification.

Boosting as a kernel-based method

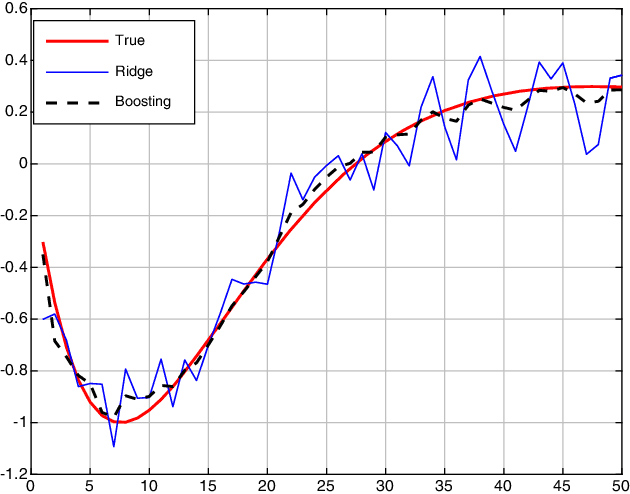
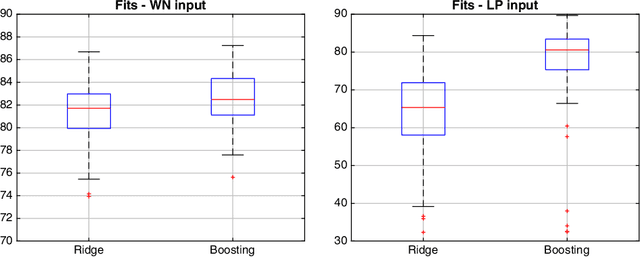
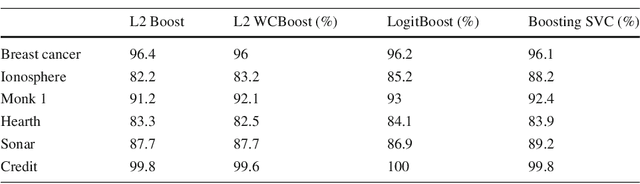
Boosting combines weak (biased) learners to obtain effective learning algorithms for classification and prediction. In this paper, we show a connection between boosting and kernel-based methods, highlighting both theoretical and practical applications. In the context of $\ell_2$ boosting, we start with a weak linear learner defined by a kernel $K$. We show that boosting with this learner is equivalent to estimation with a special {\it boosting kernel} that depends on $K$, as well as on the regression matrix, noise variance, and hyperparameters. The number of boosting iterations is modeled as a continuous hyperparameter, and fit along with other parameters using standard techniques. We then generalize the boosting kernel to a broad new class of boosting approaches for more general weak learners, including those based on the $\ell_1$, hinge and Vapnik losses. The approach allows fast hyperparameter tuning for this general class, and has a wide range of applications, including robust regression and classification. We illustrate some of these applications with numerical examples on synthetic and real data.

Blind system identification using kernel-based methods

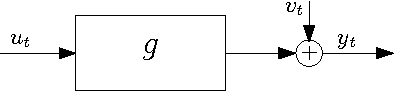
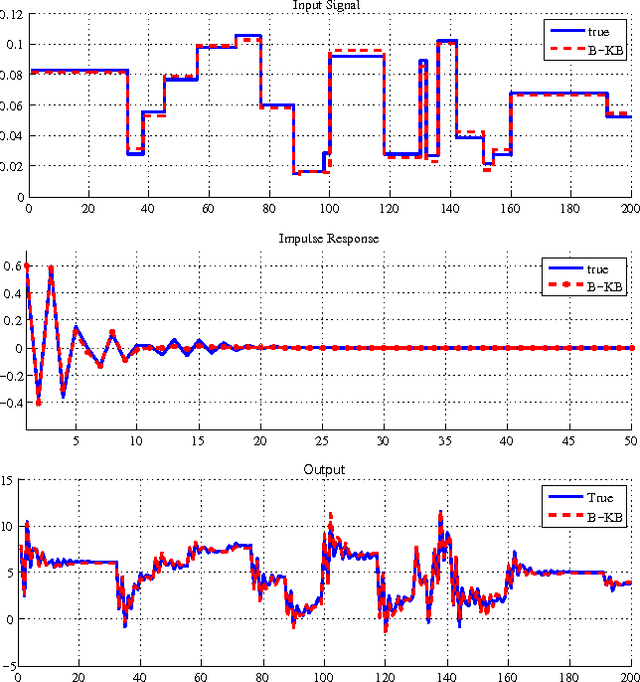
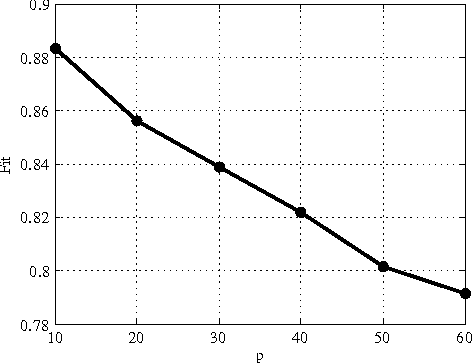
We propose a new method for blind system identification. Resorting to a Gaussian regression framework, we model the impulse response of the unknown linear system as a realization of a Gaussian process. The structure of the covariance matrix (or kernel) of such a process is given by the stable spline kernel, which has been recently introduced for system identification purposes and depends on an unknown hyperparameter. We assume that the input can be linearly described by few parameters. We estimate these parameters, together with the kernel hyperparameter and the noise variance, using an empirical Bayes approach. The related optimization problem is efficiently solved with a novel iterative scheme based on the Expectation-Maximization method. In particular, we show that each iteration consists of a set of simple update rules. We show, through some numerical experiments, very promising performance of the proposed method.

On the estimation of initial conditions in kernel-based system identification

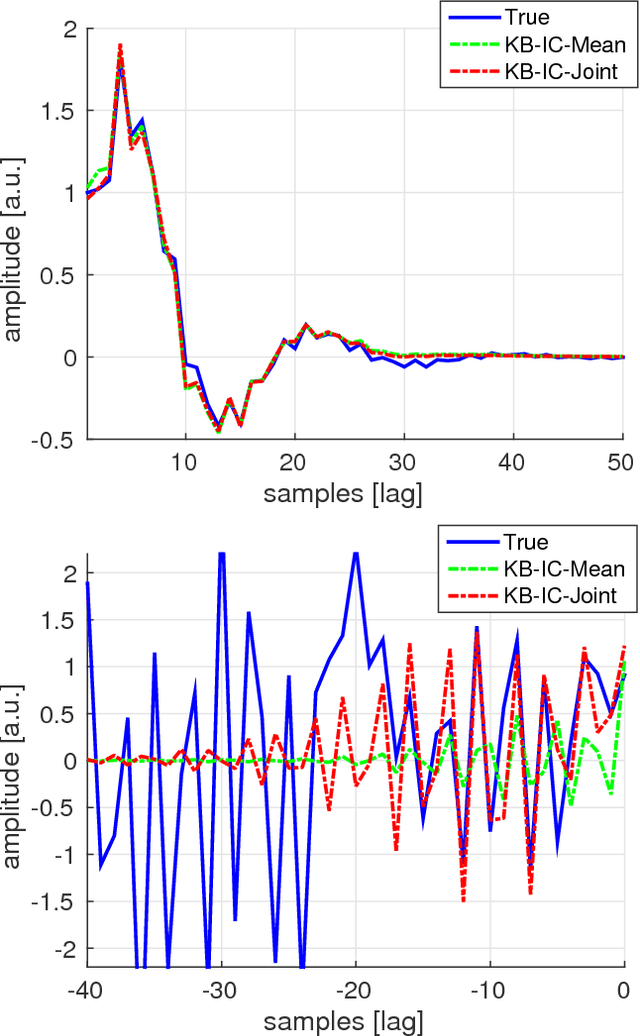
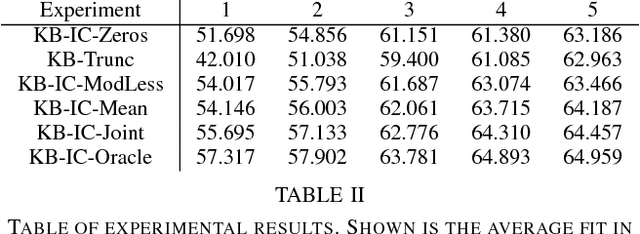
Recent developments in system identification have brought attention to regularized kernel-based methods, where, adopting the recently introduced stable spline kernel, prior information on the unknown process is enforced. This reduces the variance of the estimates and thus makes kernel-based methods particularly attractive when few input-output data samples are available. In such cases however, the influence of the system initial conditions may have a significant impact on the output dynamics. In this paper, we specifically address this point. We propose three methods that deal with the estimation of initial conditions using different types of information. The methods consist in various mixed maximum likelihood--a posteriori estimators which estimate the initial conditions and tune the hyperparameters characterizing the stable spline kernel. To solve the related optimization problems, we resort to the expectation-maximization method, showing that the solutions can be attained by iterating among simple update steps. Numerical experiments show the advantages, in terms of accuracy in reconstructing the system impulse response, of the proposed strategies, compared to other kernel-based schemes not accounting for the effect initial conditions.

A new kernel-based approach for overparameterized Hammerstein system identification

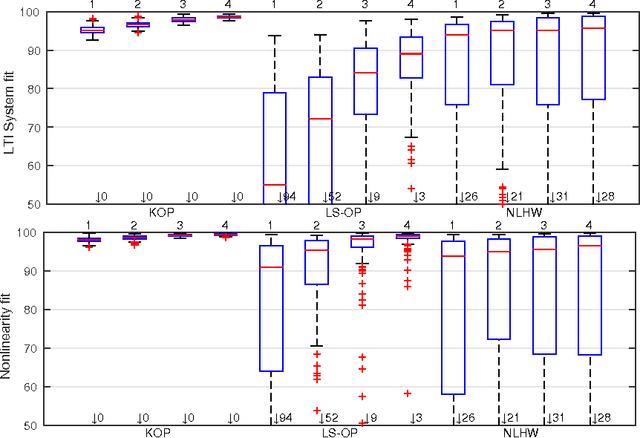
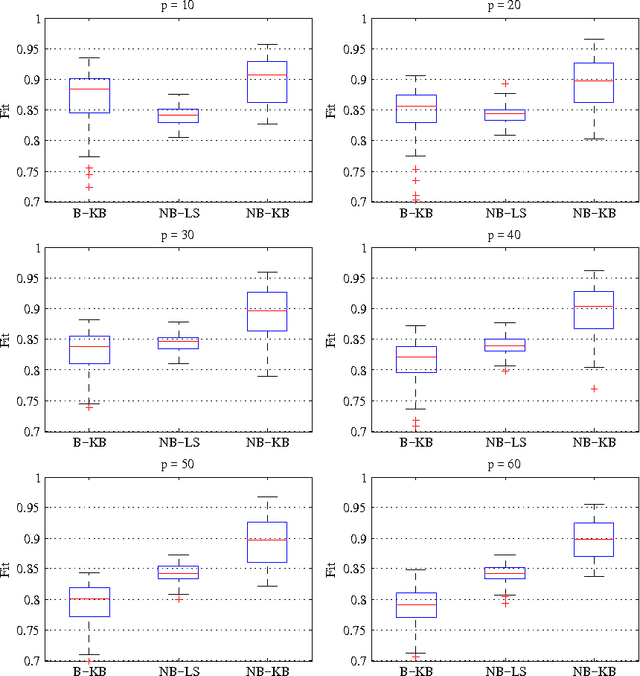
In this paper we propose a new identification scheme for Hammerstein systems, which are dynamic systems consisting of a static nonlinearity and a linear time-invariant dynamic system in cascade. We assume that the nonlinear function can be described as a linear combination of $p$ basis functions. We reconstruct the $p$ coefficients of the nonlinearity together with the first $n$ samples of the impulse response of the linear system by estimating an $np$-dimensional overparameterized vector, which contains all the combinations of the unknown variables. To avoid high variance in these estimates, we adopt a regularized kernel-based approach and, in particular, we introduce a new kernel tailored for Hammerstein system identification. We show that the resulting scheme provides an estimate of the overparameterized vector that can be uniquely decomposed as the combination of an impulse response and $p$ coefficients of the static nonlinearity. We also show, through several numerical experiments, that the proposed method compares very favorably with two standard methods for Hammerstein system identification.

Robust EM kernel-based methods for linear system identification

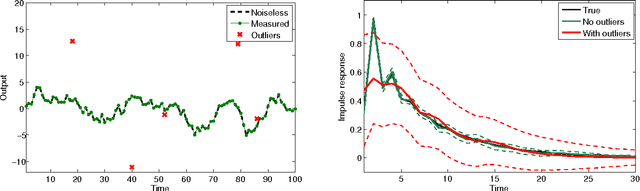
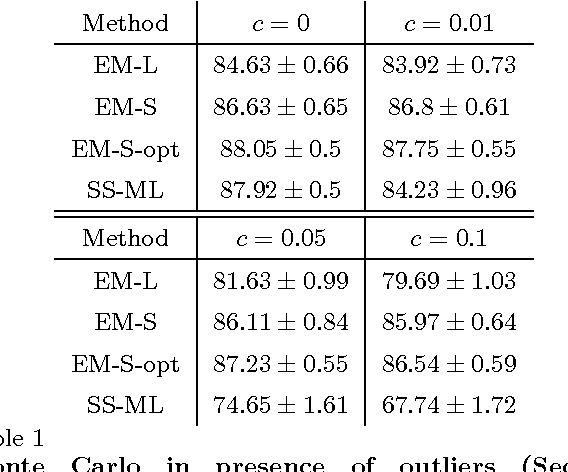
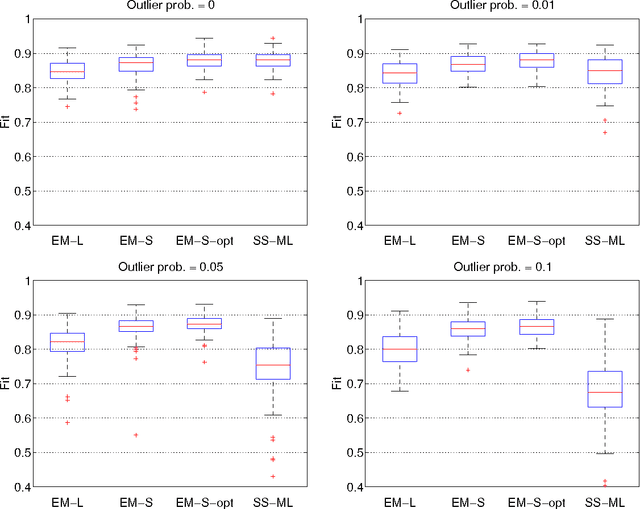
Recent developments in system identification have brought attention to regularized kernel-based methods. This type of approach has been proven to compare favorably with classic parametric methods. However, current formulations are not robust with respect to outliers. In this paper, we introduce a novel method to robustify kernel-based system identification methods. To this end, we model the output measurement noise using random variables with heavy-tailed probability density functions (pdfs), focusing on the Laplacian and the Student's t distributions. Exploiting the representation of these pdfs as scale mixtures of Gaussians, we cast our system identification problem into a Gaussian process regression framework, which requires estimating a number of hyperparameters of the data size order. To overcome this difficulty, we design a new maximum a posteriori (MAP) estimator of the hyperparameters, and solve the related optimization problem with a novel iterative scheme based on the Expectation-Maximization (EM) method. In presence of outliers, tests on simulated data and on a real system show a substantial performance improvement compared to currently used kernel-based methods for linear system identification.

Bayesian kernel-based system identification with quantized output data

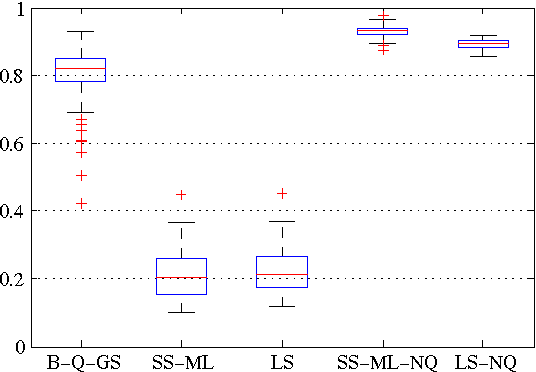
In this paper we introduce a novel method for linear system identification with quantized output data. We model the impulse response as a zero-mean Gaussian process whose covariance (kernel) is given by the recently proposed stable spline kernel, which encodes information on regularity and exponential stability. This serves as a starting point to cast our system identification problem into a Bayesian framework. We employ Markov Chain Monte Carlo (MCMC) methods to provide an estimate of the system. In particular, we show how to design a Gibbs sampler which quickly converges to the target distribution. Numerical simulations show a substantial improvement in the accuracy of the estimates over state-of-the-art kernel-based methods when employed in identification of systems with quantized data.

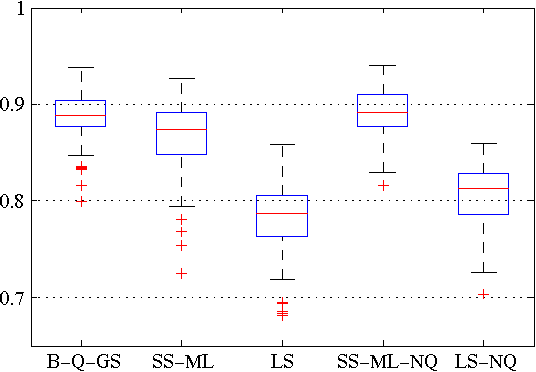
Outlier robust system identification: a Bayesian kernel-based approach

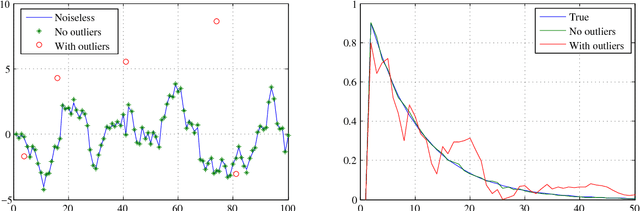
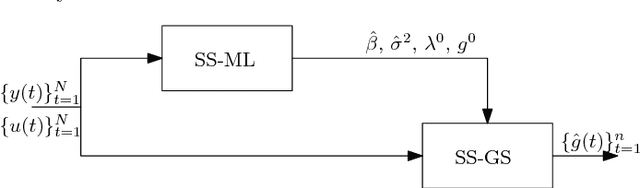
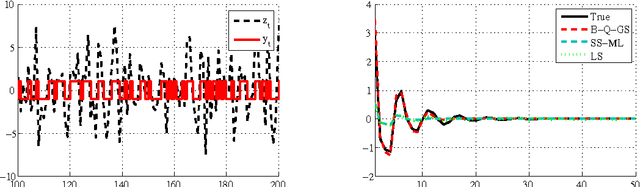
In this paper, we propose an outlier-robust regularized kernel-based method for linear system identification. The unknown impulse response is modeled as a zero-mean Gaussian process whose covariance (kernel) is given by the recently proposed stable spline kernel, which encodes information on regularity and exponential stability. To build robustness to outliers, we model the measurement noise as realizations of independent Laplacian random variables. The identification problem is cast in a Bayesian framework, and solved by a new Markov Chain Monte Carlo (MCMC) scheme. In particular, exploiting the representation of the Laplacian random variables as scale mixtures of Gaussians, we design a Gibbs sampler which quickly converges to the target distribution. Numerical simulations show a substantial improvement in the accuracy of the estimates over state-of-the-art kernel-based methods.