Hakan Hjalmarsson
Outlier robust system identification: a Bayesian kernel-based approach
Dec 24, 2013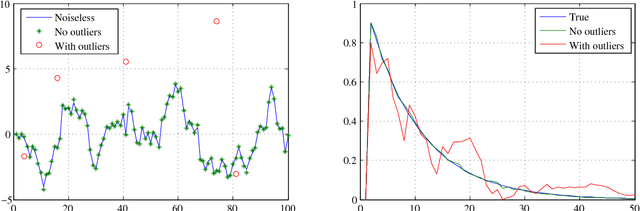
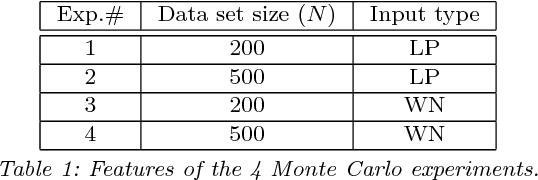
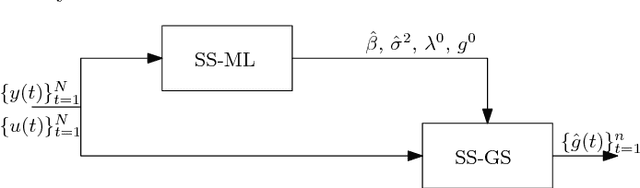
Abstract:In this paper, we propose an outlier-robust regularized kernel-based method for linear system identification. The unknown impulse response is modeled as a zero-mean Gaussian process whose covariance (kernel) is given by the recently proposed stable spline kernel, which encodes information on regularity and exponential stability. To build robustness to outliers, we model the measurement noise as realizations of independent Laplacian random variables. The identification problem is cast in a Bayesian framework, and solved by a new Markov Chain Monte Carlo (MCMC) scheme. In particular, exploiting the representation of the Laplacian random variables as scale mixtures of Gaussians, we design a Gibbs sampler which quickly converges to the target distribution. Numerical simulations show a substantial improvement in the accuracy of the estimates over state-of-the-art kernel-based methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge